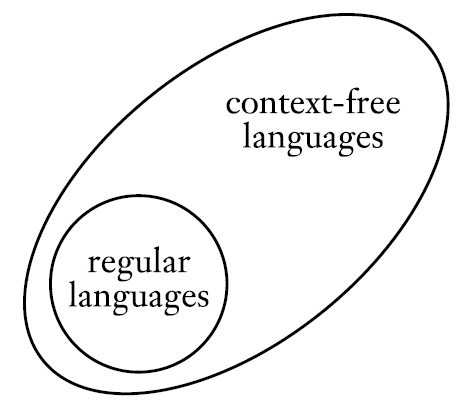
Pushdown Automata

Pushdown Automata

• 우리가 새로운 language를 배웠으므로 이에 상응하는 새로운 컴퓨터의 모델이 나온다.
• Context-Free language를 나타내는 Automata가 바로 Pushdown Automata다.
• Pushdown Automata는 NFA와 비슷하지만 추가로 stack을 하나 가지고 있다.
• stack은 유한한 정보의 공간을 가지고 있다.
• stack은 non-regular language들이 pushdown automata를 recognize하도록 도와준다.
• Pushdown automata의 power는 context-free grammar와 동일하다.
• 위의 정의는 유용한데, context-free language에 대해서 context-free grammar로 나타내든 pushdown automata로 나타내는 동일하기 때문이디.

Pushdown Automata의 구성요소와 설명

• Pushdown Automata는 다음 3가지를 가진다.
  • input tape
  • state control
  • stack
• state control은 input을 읽고 stack을 조정한다.
• input tape는 input string과 head를 나타내는 arrow를 가지고 있다. arrow를 통해서 다음 읽을 input symbol을 가리킨다.
  
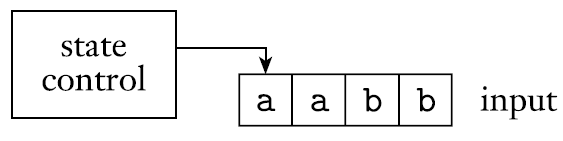
• 추가로 stack을 가지고 있다. stack또한 tape와 비슷한 모양이다.
  
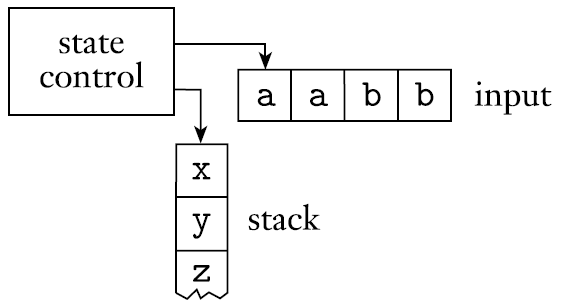
• pushdown automaton(PDA)는 symbol을 stack에 쓰고 읽을 수 있다. 다시 말해 push와 pop을 할 수 있다.
• stack에서 push는 stack의 맨 위에 symbol을 넣는다. 이를 pushing이라고 한다.
• stack에서 pop은 stack의 맨 위의 symbol을 읽어온다(읽고 꺼낸다). 이를 popping이라고 한다.
• stack이 유용한 것은 unlimited(infinite)한 정보를 저장할 수 있다는 점이다.
• input이 끝났을 때 stack이 empty하면 input을 accept한다.
• input이 끝났을 때 stack이 empty하지 않거나 stack이 empty할 때 input이 남았으면 input을 reject한다.

State diagram of PDA

• $"a,b -> c"$는 input으로 $a$가 들어오면 stack의 제일 위에 있는 symbol $b$를 $c$로 바꾸라는 뜻이다.
• $a,b,c$에 대해서 가능하며 심지어 $ε$에 대해서도 가능하다.
• $a$가 $ε$이면, input에서 어떤 symbol을 읽기 전 $b->c$를 수행한다는 뜻이다.
• $b$가 $ε$이면, stack에 $c$를 push한다.
• $c$가 $ε$이면, stack에서 $b$를 pop한다.
• PDA는 empty state를 확인하는 방법을 달리 만들어 놓지 않았다. 그러므로 $\$$를 이용한다.
  • $\$$는 input string에 없는 특별한 symbol이다.
  • 맨 처음에 stack에 $\$$를 push한다.
  • stack에서 $\$$를 pop한다는 뜻은 empty state를 확인하는 방법이다. 만약 empty state가 아니라면 $\$$는 pop되지 않을 것이기 때문에 empty state를 확인할 수 있다.

Example

$\{0^n1^n | n ≥ 0\}$

• 0이 들어올 때마다 stack에 0을 push한다.
• 1이 들어올 때마다 stack에서 0을 pop한다.
• input이 끝났을 때 stack에 0이 없어 empty하다면 input을 accept한 것이다.
• input이 끝났을 때 stac에 0이 남아있거나, stack이 empty되었는데 input이 남았으면 input을 reject한다.
  

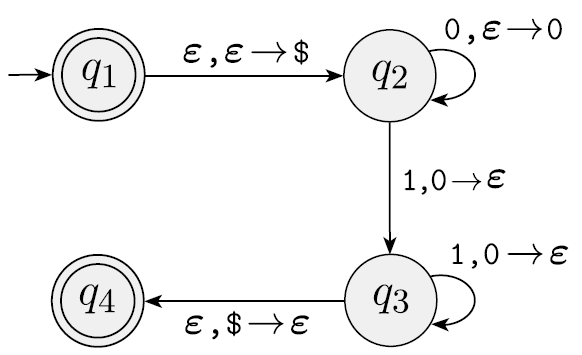
000111

• $q1-> q2$ / $ε, ε -> \$$, input : 000111, stack : $\$$
• $q2$ / $0, ε -> 0$, input : 00111, stack : $0\$$
• $q2$ / $0, ε -> 0$, input : 0111, stack : $00\$$
• $q2$ / $0, ε -> 0$, input : 111, stack : $000\$$
• $q2 -> q3$ / $1, 0 -> ε$, input : 11, stack : $00\$$
• $q3$ / $1, 0 -> ε$, input : 1, stack : $0\$$
• $q3$ / $1, 0 -> ε$, input : , stack : $\$$
• $q3 -> q4$ / $ε, \$ -> ε$, input : , stack :

00011

• $q1-> q2$ / $ε, ε -> \$$, input : 00011, stack : $\$$
• $q2$ / $0, ε -> 0$, input : 0011, stack : $0\$$
• $q2$ / $0, ε -> 0$, input : 011, stack : $00\$$
• $q2$ / $0, ε -> 0$, input : 11, stack : $000\$$
• $q2 -> q3$ / $1, 0 -> ε$, input : 11, stack : $00\$$
• $q3$ / $1, 0 -> ε$, input : , stack : $0\$$
  input이 끝났을 때 stack이 남아있으므로($\$$가 pop되지 않음)

Formal Definition of PDA

• PDA는 FA와 유사하지만, stack이 추가된 형태이다.
• 이 stack의 역할은 symbol들을 저장하는 역할이다.
• input alphabet $∑$과 stack alphabet $Γ$를 가진다.
• $∑_{ε} = ∑ ∪ \{ε\}$
• $Γ_{ε} = Γ ∪ \{ε\}$
• transition function의 공역은 $Q * ∑_{ε} * Γ_{ε}$
• 현재 상태, 다음에 들어올 input symbol, stack의 top symbol에 따른 pushdown automata의 움직임을 말해준다.
• state와 stack을 결정해야 한다. 그러므로 $Q * Γ_{ε}$
• $δ : Q * ∑_{ε} * Γ_{ε} → P(Q * Γ_{ε})$

Pushdown automaton 는 6-tuple $(Q, Σ, Γ, δ, q0, F)$이다. $Q, Σ, Γ, F$은 유한집합이다.
1. $Q$는 상태의 집합
2. $Σ$는 input alphabet
3. $Γ$는 stack alphabet
4. $δ : Q * ∑_{ε} * Γ_{ε} → P(Q * Γ_{ε})$는 transition function
5. $q0 ∈ Q$는 start state
6. $F ⊆ Q$는 accept state들의 집합이다.

$M = (Q, Σ, Γ, δ, q0, F)$는 다음을 따른다.

• input $w$는 $w = w_{1}w_{2} · · · w_{m}, w_{i} ∈ Σ_{ε}$ 로 정의할 수 있다.
• 상태들의 sequnce는 $r_{0}, r_{1}, . . . , r_{m} ∈ Q$로 정의할 수 있다.
• string들은 $s_0, s_1, . . . , s_m ∈ Γ^∗_ε$로 정의할 수 있다.
  Strings $s_i$가 $M$에 대해서 accept string이라면 아래를 따른다.

1. $r_0 = q_0$이며, $s_0 = ε$이다. $M$은 시작상태에서 시작하며 stack이 비어있어야 한다.
2. $i = 0, . . . , m − 1$에 대해서, $(r_{i+1}, b) ∈ δ(r_i, w_{i+1}, a)$를 따라야 한다. 이때 $a, b ∈ Γ_ε$와 $t ∈ Γ^*$ 에 대해서 $s_i = at$ 이며 $s_{i+1} = bt$이다. 이 말은 transition function을 따라서 다음 input이 왔을때, 현재 stack top에 따라서 state와 stack top을 바꾸라는 뜻이다.
3. $r_m ∈ F$이다. input이 끝날 때 통과상태여야한다.

Example

• $\{0^n1^n | n ≥ 0\}$
• $M1 = (Q, Σ, Γ, δ, q1, F)$이다.
• $Q = {q1, q2, q3, q4}$
• $Σ = {0, 1}$
• $Γ = {0, \$}$
• $F = {q1, q4}$
• $δ$는 아래와 같으며, 공백은 ∅과 같다.
  

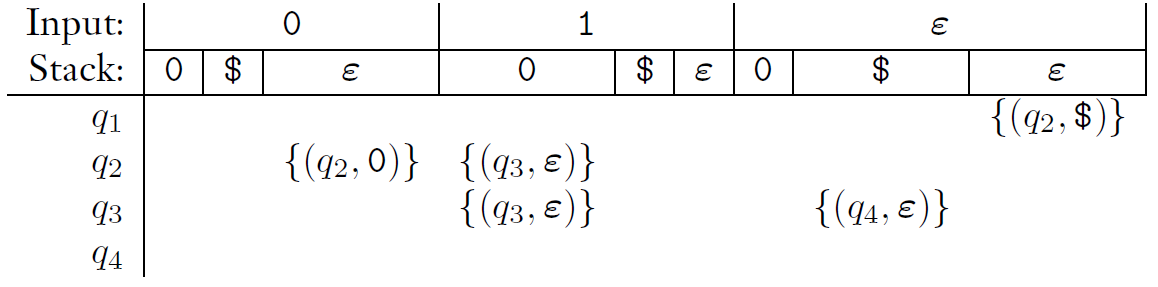
위와 똑같은 state diagram이다.

Equivalence with Context-free Grammars

• 앞에서 power가 같은 여러개가 있었다.
• DFA = NFA = Regular language등등...
• 이와 비슷하게, Context-free Grammer와 Pushdown automata는 power가 같다.

어떤 language가 context free하면 recognize하는 pushdown automaton이 존재한다. 역도 같다.

Proof

어떤 language가 context free하면 recognize하는 pushdown automaton이 존재한다.

• $A$를 CFL(Context Free Language)라고 하자.
• $A$를 통해 CFG(Context Free Grammer)를 그릴 수 있다. 이를 $G$라고 하자.
• $G$가 동일한 역할을 하는 PDA(PushDown Automata)를 $P$라고 하고 바꾸어보자.
• $P$는 입력 $w$를 accepting한다. 이 $w$는 $G$로부터 만들어졌으며, 여러가지 derivation이 있다.
• 각각의 derivation을 할 때 마다 intermediate string와 variable들을 넣어준다.
• $P$는 처음에 start variable을 stack에 push한다.
• $P$는 start variable을 넣은 후 intermediate string을 넣어준다.

• 우리는 $P$에서 중간에 있는 string을 확인해야 할 때가 있다. 그러나 PDA는 중간에 있는 string을 확인할 방법이 없다.
• 이를 위해 모든 것을 stack에 저장하지 말고 일부만 저장한다.
• 완전히 저장하지 않는 것은 아니며 저장했다가 바로 빼는 과정을 거친다.
• 이 과정을 통해 start variable을 stack의 위로 끌어올릴 수 있으며, derivation을 통해 원하는 값을 얻을때까지 반복한다.

Example

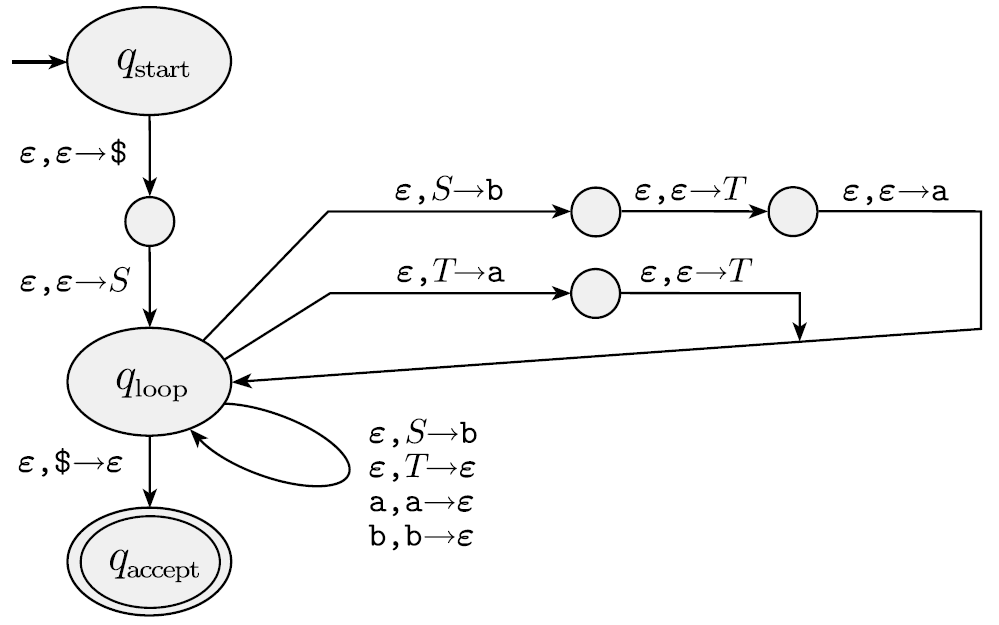
Grammer $G$는 다음과 같은 Rule을 가진다.
$S → aTb|b$
$T → Ta|ε$

• Stack에 $와 start variable $S$를 넣는다.
• 아래의 규칙에 따라 반복한다.

1. 만약 stack top이 start variable $S$라면, $S$에 대한 규칙을 하나 골라서 $S$를 context-free grammer의 오른쪽에 해당하는 값으로 바꾼다.
2. 만약 stack top이 variable $T$라면, $T$에 대한 규칙을 하나 골라서 $T$를 context-free grammer의 오른쪽에 해당하는 값으로 바꾼다.
3. 만약 stack top이 variable $a|b$라면, $a|b$를 pop한다.
4. 만약 stack top이 $라면, stack이 전부 읽혀졌을 때 accept한다.

• 이제 PDA $P = (Q, Σ, Γ, δ, q1, F)$를 정의할 수 있다.
• $Q = {q_{start}, q_{loop}, q_{accept}}$이다.
• Step1 : $q_{start}→q_{loop}$인 $ε, ε → S\$$를 만든다.
• Step2 : $q_{loop}$에 여러가지 rule에 따라서 해야할 행동들을 적어준다.
  • 기본적인 Rule은 derivation으로 만든다.
  • derivation을 만들 때 여러개를 push해야하면 뒤에 있는 것 부터 push한다.
  • $S → aTb$일 때
    • $ε, S → b$
    • $ε, ε → S$
    • $ε, ε → a$
  • push가 끝나면 $q_{loop}$로 돌아온다.
  • 각각의 symbol에 대해서 새로운 rule을 추가해준다. symbol을 pop해주는 rule이다.
    • $a, a → ε$
    • $b, b → ε$
• Step3 : $q_{loop}→q_{accept}$인 $ε, \$ → ε$를 만든다.
  

어떤 pushdown automaton이 있으면 recognized하는 context free한 language가 존재한다.

모든 regular language는 context free language이다.