Pumping Lemma

The Pumping Lemma for Regular Languages

• pumping lemma는 모든 regular language는 만족하지만 아니라면 만족하지 않는 lemma(정리)를 의미한다.
• pumping lemma를 통해 language가 P.L을 통과하지 않으면 regular language가 아님을 확인할 수 있다.
• language에 들어가는 string들은 특별한 값을 가지면 "pumped"된다. 이 string을 pumping length라고 부른다.
• pumped의 뜻은 여러번 반복될 수 있다는 뜻이다. 어떤 특정한 부분을 반복해도 여전히 string이 language안에 들어가 있을 수 있다는 의미이다.

말로는 잘 모르겠다, 정의를 보자.

Pumping Lemma

A가 regular language면, 숫자 $p$(the pumping length)가 존재한다.
만약 A안에 들어가는 string $s$가 있을 때, 모든 $s$의 길이가 $p$보다 길면, $s$는 3가지 부분으로 나눌 수 있다.
$s = xyz$는 다음과 같은 조건을 만족한다
1. 모든 i ≥ 0에 대해서, $s' = xy^iz ∈ A$
2. $|y| > 0$
3. $|xy| ≤ p$

• $|s|$은 "s의 길이"를 나타내는 기호이다.
• $y^i$는 y를 i번 conbcatenate했다는 말이다.
• $y^0$은 ε과 같다.
• s를 $xyz$로 나눌 때, x나 z는 $ε$이어도 되지만, y는 $ε$면 안된다.

Pumping Lemma의 증명

• DFA $M = (Q, Σ, δ, q1, F)$이 존재하며, language A를 recognize한다고 하자.
• pumping length p가 존재하며 M의 state만큼의 길이다.
  • $|Q| = p$
• A안에 포함되어 있는 모든 string 중 길이가 p와 같거나 큰 s가 있을때, 이 s는 어떠한 경우에도 xyz로 나눠진다.
• 만약 A안에 p와 길이가 같거나 큰 s가 없으면 어떻게 해야하는가?
  • 이런 경우에 증명은 더욱 쉽다.전제가 거짓이 되므로 답이 참이듯 거짓이든 상관없는 공허참(vacuously true)이기 때문이다.
• s가 A안에 있고, p보다 길이가 길면, s는 어떻게 되는가?
  • 아마 시작 상태인 q1에서 시작할 것이고, 마지막에는 어떠한 상태에 멈추게 될 것인데, 이 마지막 상태는 통과상태여야 한다. 왜냐하면 s가 A안에 들어가는 string이기 때문이다.
  • $s = s_1s_2s_3...s_n(n ≥ p)$일 때, 사이사이마다 어떠한 상태들을 거쳐갈 것이다.
    
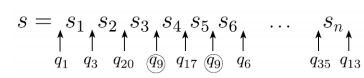
  • n의 길이를 가지는 s는, n+1개의 상태를 가질 수 있다.
  • s가 가지는 상태 개수는 상태 개수의 총합 |Q|=M보다 크다.
    • $n+1 > p$
  • 그러므로, s가 가지는 상태 개수 중 중복해서 나타나는 상태는 무조건 하나 이상이여야 한다.
• 위의 결과는 pigeonhole principle(비둘기 집 원리)의 예시이다. p개의 비둘기를 p개수보다 작은 구멍에 넣으면, 적어도 한 구멍은 2개 이상의 비둘기가 들어가 있다는 규칙이다.
  
• 우리는 이제 s를 $x,y,z$로 나눌 수 있다.
  • x는 처음부터 겹치는 상태가 처음으로 나오기 전까지의 부분
  • y는 겹치는 상태가 처음으로 나온 부분부터 두번째로 나온 부분
  • z는 겹치는 상태가 두번째로 나온 부분부터 마지막까지의 부분
• $x,y,z$를 다음과 같이 정의할 수 있다.
  • x : q1부터 q9까지 가는 부분
  • y : q9에서 출발해서 q9으로 돌아오는 부분
  • z : q9에서 출발해서 q13으로 가는 부분
    

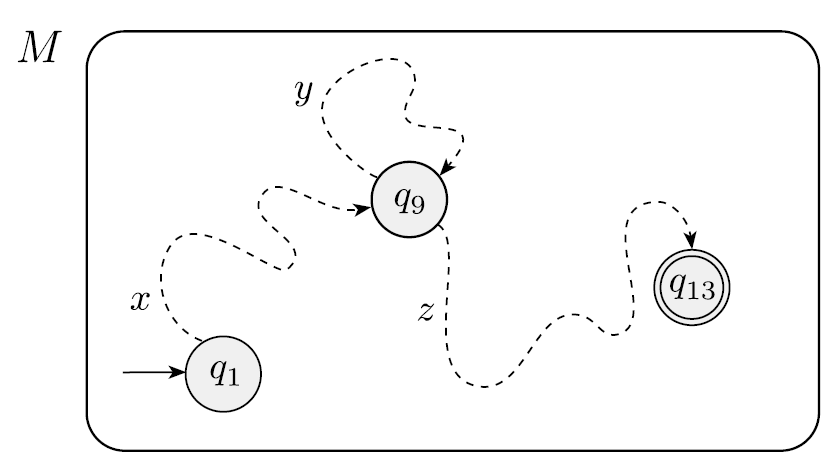
다시 조건들을 살펴보자.

1. 모든 i ≥ 0에 대해서, $s' = xy^iz ∈ A$

• x가 q1에서 q9으로, z는 q9에서 q13으로 갈 것이다. 그 사이에 y를 한번 돌든 두번 돌든 안 돌든 오천만번 돌든 상관없다. 어차피 x와 z를 거쳐서 통과상태로 갈 꺼니까! 그러므로 $s' = xy^iz$ 는 A안에 있다.

2. $|y| > 0$

• 이것이 거짓이려면 |y| < 0이거나 |y| = 0이어야 한다.
  • |y|는 길이기 때문에 음수가 나올 수 없다.
  • |y| = 0도 불가능하다. y는 상태가 중복되는 상태의 사이를 말하는 것이다. |y|가 0이라는 뜻은 중복되는 상태가 나오지 않는다는 뜻인데, 이는 위에서 본 비둘기 집 원리에 위반된다.
  • 그러므로 $|y| > 0$이어야만 한다.

3. $|xy| ≤ p$

• 위는 다시 말하면 "xy를 늘렸을 때 어디까지 커질 수 있는가?"를 물어본다.
• xy의 길이가 p가 되는 순간, 중복이 나와야 한다.
• p의 길이를 가질 때, 상태의 개수는 p+1이므로 지금까지 중복이 안 나왔으면 반드시 중복이 나와야 한다.
• 만약 xy > p가 되면, 상태의 개수는 p+1개보다 많아진다. 이 말은 중복이 적어도 하나 이상은 이미 나왔다는 소리다. 이는 x와 y의 정의에 어긋난다.
• 그러므로 $|xy| < p$다.