Regular Expression
- 우리는 수학에서 +와 ×같은 연산자들을 사용해서 식을 만들 수 있다. 마치 (5 + 3) × 4처럼.
- 마찬가지로, language에서 regular operation을 통해서 식을 만들 수 있으며, 그 식을 regular expression이라고 부른다.
- (0 ∪ 1) ◦ 0* 같은 예시가 나올 수 있다.
- 앞쪽은 0or1을 꺼내고, 뒤는 0을 여러번 쓸 수 있는 language를 나타낸다.
- 심볼 0과 1은 사실 {0}과 {1}을 줄여 쓴 것이다. 그러므로 (0 ∪ 1)은 ({0} ∪ {1})의 의미이다.
- Concatenation symbol ◦은 대부분 생략된다. (0 ∪ 1)0∗ 과 (0 ∪ 1) ◦ 0은 같다.
- 어떤 패턴이 포함되어 있는 string을 찾고 싶을 때 regular expression을 이용해서 찾을 수 있다.
- C같은 프로그래밍 언어에서 어떠한 line이 주어졌을 때, 그 line이 문법에 맞는지 확인 할 때도 유용하게 쓰인다.
(0 ∪ 1)∗
이것이 의미하는 건 0과 1로 이루어진 모든 string을 말한다.
Σ = {0, 1}일 때, (0 ∪ 1) 라는 식으로 표현할 수 있다.
더 나아가서, Σ가 alphabet일때, Σ*는 Σ가 표현할 수 있는 모든 string을 가지고 있는 alphabet이다.
Formal Definition
R이 다음과 같은 조건을 만족하면 regular expression이라고 할 수 있다.
- alphabet Σ 안에 있는 a
- ε
- ∅
- (R1 ∪ R2), R1과R2는 regular expressions
- (R1 ◦ R2), R1과R2는 regular expressions
- (R1)*, R1은 regular expression
- 1, 2는 {a}와 {ε}에 대한 regular expression이며, 한 글자일 때를 말한다.
- 3은, empty language에 대한 regular expression이며, 글자가 없을 때를 말한다. ∅과 ε를 헷갈리면 안된다.
- 4, 5, 6은 R1과 R2가 어떠한 이유에서든지 regular expression이면, Union, Concatenation, Star연산은 모두 regular expression이라는 의미이다.
- 1,2,3은 수학적 귀납법의 Base에 해당하고, 4,5,6은 수학적 귀납법의 Step에 해당한다.
- 연산자들의 계산 순서는 star, concatenation, union순서로 계산하며, 계산 순서에 영향을 주지 않는 괄호는 생략할 수 있다.
- R+는 RR∗을 줄인 것으로, ε을 포함하지 않는다. 다시 말해 0번 star하는 것은 허용하지 않겠다는 뜻이다. 이에 따라 R+ ∪ ε = R∗라고 말할 수 있다.
- R은 단순한 식을 의미하는 것으로, language는 L(R)로 표시할 수 있다.
여러가지 예시
-
0∗10∗ = {w | w는 1을 딱 하나만 가지고 있다}.
-
Σ∗1Σ∗ = {w | w는 1을 적어도 하나는 가지고 있다}.
-
Σ∗001Σ∗ = {w | w는 001을 substring으로 가지고 있다}.
-
1∗(01+)∗ = {w | 모든 0은 바로 뒤에 1을 적어도 하나는 가지고 있다}.
-
(ΣΣ)∗ = {w | w는 길이가 짝수이다.}.
-
(ΣΣΣ)∗ = {w | w는 길이가 3의 배수이다}.
-
01 ∪ 10 = {01, 10}.
-
0Σ∗0 ∪ 1Σ∗1 ∪ 0 ∪ 1 = {w | w는 처음과 끝이 같은 심볼이다}.
-
(0 ∪ ε)1∗ = 01∗ ∪ 1∗.
0 ∪ ε == {0, ε}이며 concatenation 1∗은 0과 ε에 적용된다. -
(0 ∪ ε)(1 ∪ ε) = {ε, 0, 1, 01}.
-
1∗∅ = ∅.
- Concatenating은 앞에서 꺼내오고, 뒤에서 꺼내와서 서로 붙히는 연산이다.
- 예를 들어, {0,11,000}{1,00}은 앞에 3개, 2에 2개를 꺼내와서 붙히는 것이므로 3x2 = 6개의 경우가 나온다.
- 다시 돌아와서, 1*은 ε,1,11,111...이고, ∅은 ∅다. infinite x 0 = 0가 나온다.
-
∅∗ = {ε}.
- Star operation은 주어진 language에서 아무거나 뽑는 것이다. 만약 language가 비었으면 star operation은 0개를 뽑으며 이것은 {ε}가 같다.
Regular Expression Identities
- If we let R be any regular expression, we have the following identities.
- R ∪ ∅ = R.
- empty language를 Union하면 변화가 없다.
- R ◦ ε = R.
- ε를 Concatenation하면 변화가 없다.
- 그러나, 앞에 식들에서 ∪,◦를 바꾸거나 ∅,ε를 바꾸면 달라진다.
- R ∪ ε may not equal R.
- R = 0이면, L(R) = {0}이지만 L(R ∪ ε) = {0, ε}다.
- R ◦ ∅ may not equal R.
- R = 0이면, L(R) = {0}이지만 L(R ◦ ∅) = ∅다.
활용성
프로그래밍 언어에서 사용됨
- 숫자를 입력받을 때, 입력받는 값에 대한 검사를 한다.
- D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}일때(10진수의 symbols)
(+ ∪ − ∪ ε)(D+ ∪ D+.D∗ ∪ D∗.D+)라는 검사를 한다.
- 앞에 부호 +,-가 오거나 없어야 한다.
- 뒤에는 숫자가 하나 오거나, 숫자가 하나 이상 있고 Point(.)뒤에 숫자가 여러개가 있거나, 숫자가 여러개가 있고 Point(.)뒤에 숫자가 하나 이상 있어야 한다.
72, 3.14159, +7., −.01같은 예시들
식을 이용하여 검사를 할 수 있다. 컴파일러에서 이런 활동을 하는 자동 시스템을 "lexical analyzer"라고 부른다.
Regular Expression과 Finite Automata는 같다
Regular Expression은 연산자의 조합과 식으로 이루어진 특성들로 인해 Finite Automat와 달라 보인다. 그러나 둘은 사실 같다. Regular Expression은 Finite automaton으로 치환할 수 있으며, Finite automaton이 어떠한 language를 recognize하면, 그에 해당하는 Regular Expression이 존재한다.
A language is regular if and only if some regular expression describes it.
어떤 language가 regular일때, 그것을 describe하는 어떤 regular expression이 존재한다. 반대도 가능하다.
수학적 귀납법으로 증명
증명 아이디어
If a language is described by a regular expression, then it is regular.
- regular expression R이 어떠한 language A를 describe한다.
- R을 A를 recognize하는 NFA로 바꾸면 된다.
- 그렇게 하면, NFA는 A를 recognize하게 되고, A는 regular language가 된다.
- Regular expression은 무한개가 있지만, 만드는 방법은 6가지밖에 없다. 이를 이용하면 증명할 수 있다.
증명
임의의 regular expression R을 NFA N으로 변환해보자. R의 formal definition에 따라 6가지 방법으로 나온다.
-
alphabet Σ 안에 있는 a
L(R) = {a}이고, NFA는 L(R)을 recognize한다.
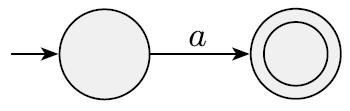
N = ({q1, q2}, Σ, δ, q1, {q2}), δ(q1, a) = {q2}, r != q1, or b != a 일때 δ(r, b) = ∅ -
ε
L(R) = {ε}이고, NFA는 L(R)을 recognize한다.
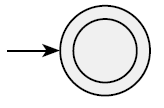
-
∅
L(R) = ∅,이고, NFA는 L(R)을 recognize한다.
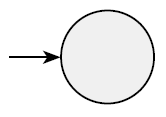
-
(R1 ∪ R2), R1과R2는 regular expressions
-
(R1 ◦ R2), R1과R2는 regular expressions
-
(R1)*, R1은 regular expression
4,5,6번은 Regular Operation을 NFA로 정의하는 방법에 따라 증명할 수 있다. 여기서 알아보자.
그러므로 Regular Expression을 NFA로 정의할 수 있으므로 증명된다.
예시
다음은 (ab ∪ a)∗를 NFA로 나타낸 것이다.
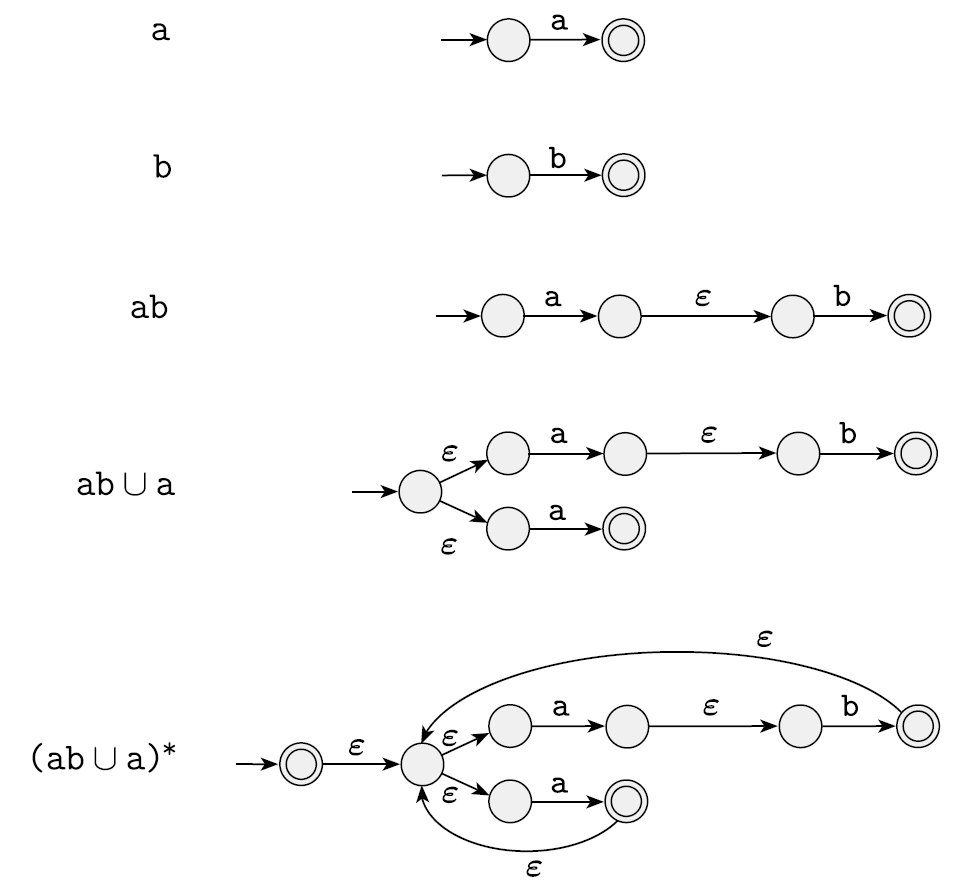
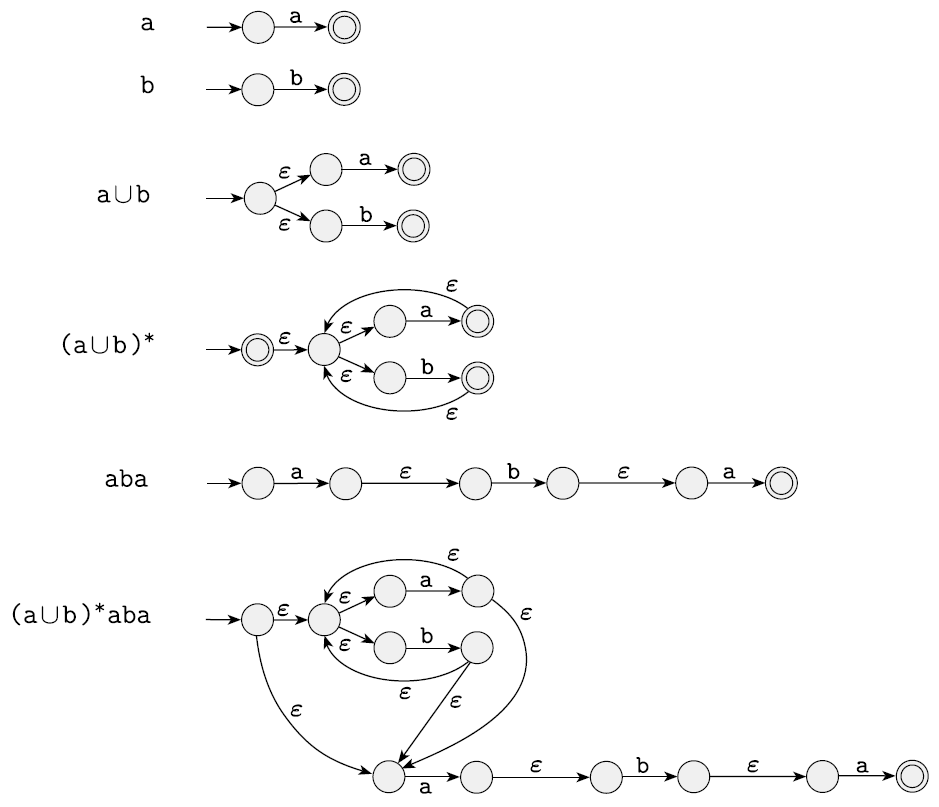
다음은 (a ∪ b)∗aba를 NFA로 나타낸 것이다.
증명
If a language is regular, then it is described by a regular expression.
- language A가 regular면, describe하는 regular expression가 있다.
- 왜냐하면 A를 accept하는 DFA가 있기 때문이다.
- DFA가 reuglar expression과 같다는 것을 증명한다.
- 그 후 GNFA를 사용한다.
- 정리하면, A를 accept하는 DFA를 GNFA로 바꾸고, GNFA를 regular expression으로 바꾼다.
- regular language A에 해당하는 DFA가 있고, DFA와 정확히 일치하는 GNFA가 있으며, GNFA와 정확이 일치하는 regular expression이 있다.
- 그러므로 regular language가 있으면 describe하는 regular expression이 존재한다.
