Regular Languages

컴퓨터가 무엇인가?

"컴퓨터가 무엇인가?" 라고 하면 한마디로 정의하기엔 힘들 것이다.

• PC나 노트북, 핸드폰등은 컴퓨터인가? 그럴 것이다.
• 펜이나 전등은 컴퓨터라고 할 수 없을 것이다.
• 그렇다면 리모컨은? 인터폰은?

좁은 의미의 컴퓨터는 소프트웨어와 하드웨어로 구성되어 있으며, 안에 있는 소프트웨어를 바꾸면 다른 일을 수행할 수 있는 것을 말한다. 이 과목에서는 넓은 의미의 컴퓨터로 들어가 전자회로 수준의 기계도 컴퓨터라고 부를 것이다.

우리가 생각하는 이상적인 컴퓨터를 컴퓨테이셔널 모델이라고 부른다.

제일 간단한 모델부터 시작할건데, finite state machine 또는 finite automata라고 부른다.

Finite automata(유한 오토마타)

유한 오토마타는 제한된 양의 메모리를 가지고 있다. 여기서 제한되었다는 말은 유한(finite)적이라는 말이다. 유한 오토마타는 전자회로들의 중심이 되는 모델이다.

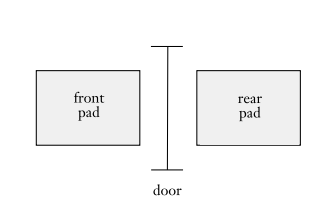
컨트롤러가 있는 자동문을 예시로 들어보자.

• 앞에 패드가 있어서 사람이 오는지를 확인할 수 있다.
• 뒤에도 패드가 있어서 사람이 뒤에 있으면 열리지 않게 해서 문이 사람을 때리지 않게 한다.
  
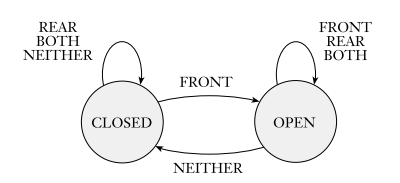
• 컨트롤러는 두개의 상태를 가지고 있다. "OPEN" 또는 "CLOSED"
  • CLOSED 상태에서 OPEN으로 가는 상태는 앞에 사람이 있는 FRONT상태밖에 없다.
  • OPEN 상태에서 CLOSED로 가는 상태는 둘다 사람이 없는 NEITHER상태밖에 없다.
  • 나머지는 지금 상태를 유지한다.

예시로, 입력을 FRONT, REAR, NEITHER, FRONT, BOTH, NEITHER, REAR, and NEITHER로 받았다고 하자.
상태는 CLOSED (starting), OPEN, OPEN, CLOSED, OPEN, OPEN, CLOSED, CLOSED, 그리고 CLOSED순으로 변경된다.

FINITE AUTOMATAN에 대응하는(counterpart) 모델로 Markov chains라는 게 있는데, 상태에 확률이 들어가는 모델이다.

• 1의 개수가 홀수인 유한 오토마타를 생각해보자.
• q0 : 1의 개수가 짝수인 상태
• q1 : 1의 개수가 홀수인 상태
• q0에서의 상태 변화 : 0을 만나면 상태를 유지하며 1을 만나면 q1으로 이동한다.
• q1에서의 상태 변화 : 1을 만나면 상태를 유지하며 0을 만나면 q0으로 이동한다.
  
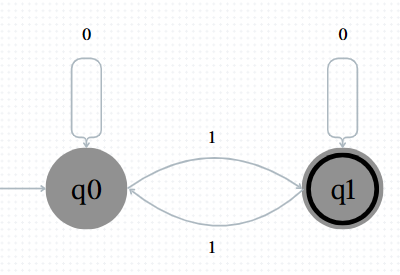
• 예를 들어 011100이 들어오면, 상태는 q0(starting) -> q0 -> q1 -> q0 -> q1 -> q1 -> q1(end)가 되며, q1은 accept state이므로 011100에 대한 이 유한 오토마타의 결론은 Accept가 된다.

이런 기계장치에 language가 들어오면, 상태로 판별해준다. 다시 말하면 어떤 문제(language)의 답이면서 컴퓨터로 구현할 수 있는 장치인 것이다.

• q1, q2, q3의 상태가 있는 유한 오토마타 M이 있다.
• 시작 상태인 q1은 input을 받아서 다른 곳으로 보내준다.
• accept state q2는 이중 원으로 나타낸다.
• 다른 상태로 가는 것을 transitions라고 부른다.
• 1101같은 string을 받으면, output(결과)를 내는데, 그것이 accept인지, reject인지를 판별해준다.
• 유한 오토마타 M은 Accept는 input이 q2상태에 멈추면 Accept라고 말한다.
  

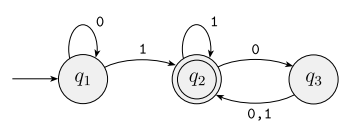
  이 오토마타는 1이 한번 이상 나오고, 마지막 1 뒤에 있는 0의 개수가 짝수인 string들을 Accept하는 오토마타이다.

유한 오토마타의 정의

5-tuple$(Q, Σ, δ, q0, F)$로 구성된 유한 오토마톤(finite automation)는 다음과 같다.
1. $Q$는 유한한 상태들의 집합이다.
2. $Σ$은 유한한 심볼(alphabat)들의 집합이다.
3. $δ : Q × Σ → Q$ 는 transition function인데, Q와 E의 멱집합을 정의역(domain)으로 가지고, $Q$를 공역(range)으로 가지는 함수이다.
4. $q0 ∈ Q$ 는 시작 상태(start state)이다.
5. $F ⊆ Q$ 통과 상태(accept state)이다.

• $δ$는 함수이므로, 한개의 상태(값)만을 가져야 한다.
• $F$안에 통과 상태가 아무것도 없어도 가능하다.

위 예시를 $M1$이라는 오토마타로 정의해보면
$M1 = (Q, Σ, δ, q0, F)$
1. $Q = {q1, q2, q3}$
2. $Σ = {0,1}$
3. $δ : {q1, q2, q3} × {0,1} → {q1, q2, q3}$

	q1	q2	q3
0	q1	q3	q2
1	q2	q2	q2

4. $q1 ∈ Q$
5. $F = {q2} ⊆ Q$

오토마타 $M$이 통과시키는 모든 문자열을 $A$라고 했을 때, $A$는 $M$이라는 기계의 언어(language of machine)이라고 하고, $L(M) = A$로 표시한다. 그리고 $M$이 $A$를 recognizes(accepts)한다고 말한다.

예를 들어, $A$ = {$w$ | $w$가 1을 적어도 하나라고 포함하고, 마지막 1 뒤에 나오는 0의 개수가 짝수인 문자열}일때, $L(M1) = A$라고 한다.

예시들

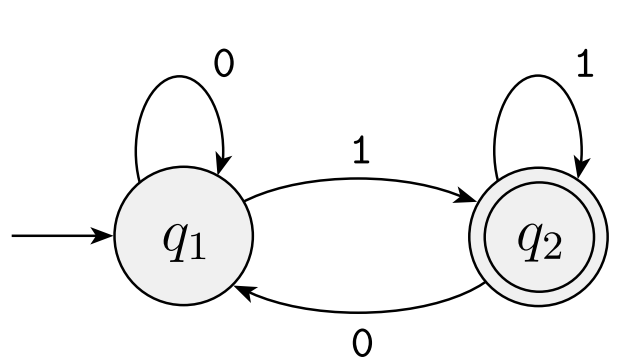
• M2 = ({q1, q2}, {0,1}, δ, q1, {q2})

• 	0	1
  q1	q1	q2
  q2	q1	q2

• L(M2) = {w | w는 1로 끝난다}

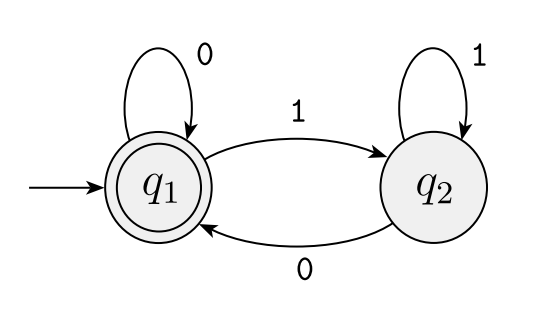
• M3 = ({q1, q2}, {0,1}, δ, q1, {q1})

• 	0	1
  q1	q1	q2
  q2	q1	q2

• L(M2) = {w | w는 empty string(빈 문자열)이거나 0으로 끝난다}

주의해야 할 부분은 M2와 M3가 반대가 아니라는 것이다. M3를 empty string도 통과시킨다.

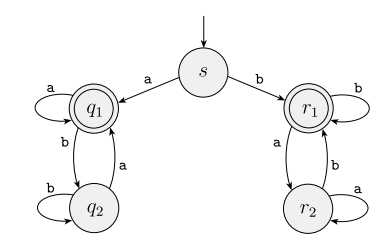
• M4 = ({s, q1, q2, r1, r2}, {a, b}, δ, s, {q1, r1})

• 	a	b
  s	q1	r1
  q1	q1	q2
  q2	q1	q2
  r1	r2	r1
  r2	r2	r1

• L(M4) = {w | w는 문자가 1개 이상 있고, a로 시작하면 a로 끝나고, b로 시작하면 b로 끝나는 문자열이다.}

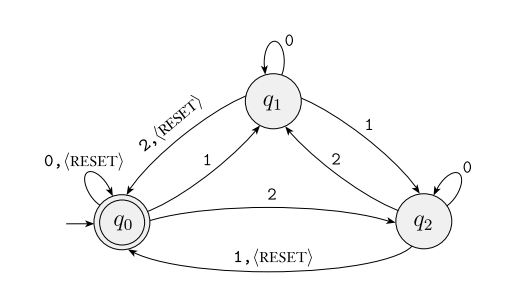
• M4 = ({<RESET>q0, q1, q2}, {0, 1, 2}, δ, q0, {q0})

• 	RESET	0	1	2
  q0	q0	q0	q1	q2
  q1	q0	q1	q2	q0
  q2	q0	q2	q0	q1

• 모든 state는 0을 만나면 가만히 있고, 1을 만나면 1칸 전진하며, 2를 만나면 2칸 전진한다.(1칸 후진한다)
• RESET을 만나면 값을 0으로 만든다.(q0으로 돌아간다)
• L(M4) = {w | w는 나오는 모든 문자열을 더한 수를 3으로 나누었을 때 나머지가 0인 문자열이다(3의 배수가 되는 문자열이다)}