Formal Definition of Computation

유한 오토마타가 하는 일

유한 오토마타가 하는 일을 수학적으로 나타낸다.

M = (Q, Σ, δ, q0, F)이 주어지고, $w = w_{1}w_{2} · · · w_{n}$을 심볼으로 가지는 알파벳 Σ가 있다. Q를 참조하는 시퀀스 $r_{0}, r_{1}, . . . , r_{n}$ 들이 다음의 조건을 만족할 때 M은 w를 recognize한다.

1. $r0 = q0$
2. $δ(r_{i}, w_{i+1}) = r_{i+1}, i = 0, . . . , n − 1,$ and
3. $r_{n} ∈ F$

하나씩 파고들어보자.

1. r0 = q0라는 말은 첫번째 상태가 시작 상태가 되어야 한다는 것을 의미한다. 시작할 때는 q0의 상태여야 한다는 소리다.

2. rn ∈ F라는 말은 마지막 상태가 통과 상태 중 하나가 되어야 한다는 것을 의미한다. M이 w를 recognize하려면 마지막 상태는 통과 상태여야만 하고, 그렇지 않으면 M은 w를 recognize하지 않는다.

3. δ(ri, wi+1) = ri+1, for i = 0, . . . , n − 1 가 복잡하게 느껴질 수 있는데, 이해하면 간단하다. δ라는 함수 안에 i번째 상태를 넣고, i+1번째 심볼을 넣으면 i+1번째 상태가 된다는 소리다. 이해가 어려운가? 지금 상태와 다음 심볼을 넣으면 다음 상태가 된다는 의미랑 똑같다. 상태가 바뀌는 것은 순차적으로 이루어져야 하며, δ라는 함수에 넣었을 때 예외가 나와서는 안된다는 소리이기도 하다.

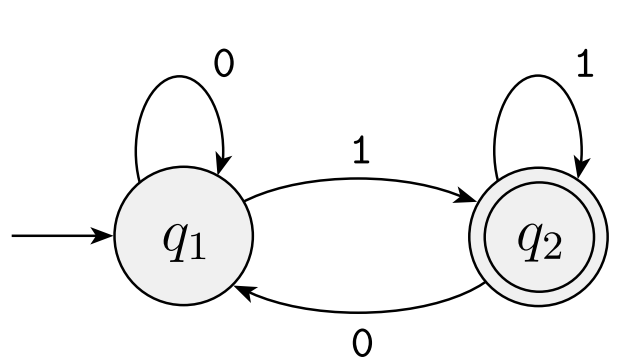
• M2 = ({q1, q2}, {0,1}, δ, q1, {q2})

• 	0	1
  q1	q1	q2
  q2	q1	q2

• L(M2) = {w | w는 1로 끝난다}

이런 예시가 있다고 해보자.
w = 0110011일때
1. r0 = q1(시작 상태)
2. δ(ri, wi+1) = ri+1, for i = 0, . . . , n − 1
(r0(q1), w1(1)) = r1(q2), (r1(q2), w2(1)) = r2(q2) 등등..
3. r7(q2) ∈ F = {q2}.

Regular language

M = (Q, Σ, δ, q0, F)이 주어지고, w = w1w2 · · · wn을 심볼으로 가지는 알파벳 Σ가 있다. Q를 참조하는 시퀀스 r0, r1, . . . , rn 들이 다음의 조건을 만족할 때 M은 w를 recognize한다.

1. r0 = q0
2. δ(ri, wi+1) = ri+1, for i = 0, . . . , n − 1, and
3. rn ∈ F.

어떠한 유한 오토마나가 recognizes하는 language를 regular language라고 한다.

Designing Finite Automata

• 오토마톤을 디자인 하는 것은 creative process다. 조각하기를 생각해보자. 어떤 사람들 머리부터 조각할 거고 어떤 사람은 다리부터 조각할 것이다. 그러나 결과는 모두 같을 것이다. 과정부터 잘 생각하는 창조적인 활동이라는 것이다.
• 당신이 머신이 되어서 머신이 어떻게 해야 할 지를 생각해보라
• finite automata를 recognize할 수 있는 어떤 language를 생각해보아라.
• 그 language에 해당 될 것 같은 문자열을 생각해봐라
• 생각한 문자열에 대해서, 전체적으로 생각하지 말고 symbol 하나하나를 생각해보아라.
• 이 문자열이 language 안에 들어갈 수 있는 지 판단해라.
• 내가 분석을 하면서 중요하게 기억해야 할 점은 무엇인지를 파악해라.

Designing Example

예시 만들어보기

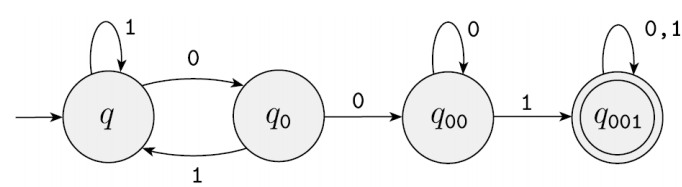
E2는 001을 포함하는 regular language를 recognize한다.

• 예를 들어, 0010, 1001, 001, 11101100011111은 통과하지만, 11, 0000은 통과 못한다.

• 001이 나오면, 이후 나오는 모든 과정을 스킵한다.

• 0이 나오면, 001의 첫번째이므로 지나간다.

• 다음 1이 나왔을때, 0이 부족하므로 처음으로 돌아간다.

• 다음 0이 나오면, 001의 두번째이므로 지나간다.

• 이제 001이 될때까지(1이 나올때까지) 반복한다.

• 만약 001이 나왔으면, 그 string을 recognize하는 거다.

• 그러므로 4개의 가능성이 있다.
  1. 처음 상태(아무거나 나와야함)
  2. 0을 본 상태
  3. 00을 본 상태
  4. 001을 본 상태

• 이로 인해 상태 q, q0, q00, q001이 있다는 것을 알 수 있다.
  q에서 1을 만나면 다시 자신으로 돌아오고, 0를 만나면 q0로 간다.
  q0에서 1을 만나면 q로 돌아가고, 0을 만나면 q00로 간다.
  q00에서 1을 만나면 q001로 가고, 0를 만나면 자신으로 돌아온다.
  q001은 0이든 1이든 자신으로 돌아온다.

E2 = ({q, q0, q00, q001}, {0,1}, δ, q, {q001})

	0	1
q	q0	q
q0	q00	q1
q00	q00	q001
q001	q001	q001