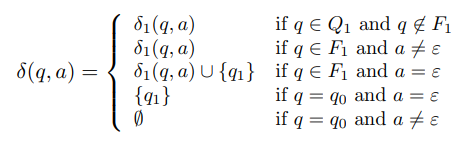계산 이론의 연산자
수학에서는 계산에 대해서, 편하게 나타내기 위한 도구로 연산자를 사용한다. +,-,*,/ 는 대표적인 연산자다.
이와 비슷하게, regular language에 대해서 연산을 할 수 있는 연산자 3개를 알아보자.
A와 B가 language들일때, 우리는 union, concatenation, star라는 연산자를 정의할 수 있다.
- Union : A ∪ B = {x | x ∈ A or x ∈ B}.
- Concatenation :A ◦ B = {xy | x ∈ A and y ∈ B}.
- Star : A = {x1x2 . . . xk | k ≥ 0 and xi ∈ A}.
- ε는 A가 무엇이든간에 A*에 포함된다.
연산자 사용 예시
Σ는 26개의 심볼 {a, b, . . . , z}의 집합인 alphabet이라고 하자. 만약 A = {good,bad} 이고 B = {boy, girl}면
- A ∪ B = {good, bad, boy, girl},
- A ◦ B = {goodboy, goodgirl, badboy, badgirl}
- A∗ = {ε, good, bad, goodgood, goodbad, badgood, badbad,
goodgoodgood, goodgoodbad, goodbadgood, goodbadbad, . . . }
여기서 중요한 건, operate를 했을 때 나오는 결과물은 똑같이 regular language이다. 다시 말해, 이 3가지의 operate는 closed 되어있다는 소리다. 더 복잡한 것을 만들기 위해서, 작은 것들의 단위로 쪼개서 나중에 합해도 똑같은 결과가 나오는데, 이것을 증명하기 위해서는 operate가 closed 되어있다는 것을 증명해야 한다.
A ∪ B를 한 뒤, ◦ C를 해도 여전히 결과물은 regular language다.
증명들
증명 전 M1과 M2라는 예시를 가지고 증명할 예정이다.
M1은 1의 개수가 짝수인 language를 recognize하는 오토마톤이다.
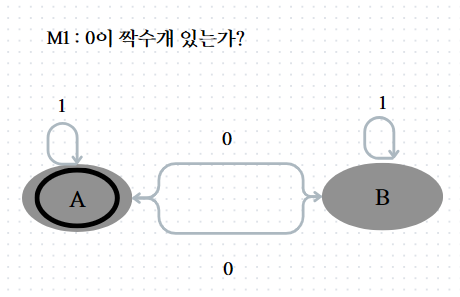
M2는 0의 개수가 짝수인 language를 recognize하는 오토마톤이다.
Union operation
- The class of regular languages is closed under the union operation.
- In other words, if A1 and A2 are regular languages, so is A1 ∪ A2.
증명 아이디어
- A1 과 A2 는 regular이며, 우리는 어떠한 유한 오토마타 M1이 A1을 recognize하고, 유한 오토마타 M2가 A2를 recognizes하는 것을 알고 있다.
- A1 ∪ A2 가 regular라는 것을 증명하기 위해 우리는 M이라는 유한 오토마타가 있는 것을 가정하고, M이 A1 ∪ A2를 recognize한다고 해야 한다.
- M을 M1과 M2로 표현해야 한다.
- 오토마타 M은 M1이나 M2가 통과시키는 것을 통과시켜야 한다.
- 그러므로 어떤 string에 대해서 M1과 M2를 시도해서 둘 중 하나를 통과하는 것을 확인한다.(이 과정을 simulating이라고 한다.)
- M1 먼저하고 M2를 나중에 하거나, 반대의 경우는 성립하지 않는다.
- 이것은 구조적인 문제로, string의 head는 지나간 후에 돌아오지 않는다.
- 그러므로, M1과 M2를 동시에 시도해야 한다.
- M1은 k1개의 상태를 가지고 있고, M2는 k2개의 상태를 가지고 있을 때, M은 k1 X k2개의 상태를 가지고 있다.
- M은 pair에서 pair로 가며, 각각의 pair는 M1의 상태와 M2의 상태를 가지고 있다.
- M의 accept state는 M1의 accept state거나 M2의 accept state가 있어야 한다.
증명
-
M1는 recognize A1하고, M1 = (Q1, Σ, δ1, q1, F1)이다. M2는recognize A2하고, M2 = (Q2, Σ, δ2, q2, F2)이다.
-
A1 ∪ A2를 recognize하는 M은 M = (Q, Σ, δ, q0, F)이다.
-
Q = {(r1, r2) | r1 ∈ Q1 이고 r2 ∈ Q2}.
-
Q는 Q1과 Q2의 멱집합이며, Q1 × Q2로 쓰인다.
-
Σ은 알파벳이며 M1와 M2랑 똑같다.
-
만약 Σ1과 Σ2처럼 달라도 연산자는 논리적으로는 성립한다.(증명 가능하다)
-
q0는 (q1, q2)의 pair다. 다시 말해 M1과 M2의 시작 상태를 합한 상태다.
-
δ는 정의를 따르는 함수이다.
-
상태 (r1, r2) ∈ Q 와 심볼 a ∈ Σ에 대해서, δ((r1, r2), a) = (δ1(r1, a), δ2(r2, a))다.
-
다시 말해, (,)인 δ가 있다. 앞은 r1이 a를 만나면 어디로 가는지를 나타냈으며 이것은 δ1(r1,a)와 같다. 뒤는 r2가 a를 만나면 어디로 가는지를 나타으며, 이것은 δ2(r2,a)와 같다. 그러므로 δ = (δ1(r1, a), δ2(r2, a))다.
-
F는 M1의 accept state거나 M2의 accept state여야 한다.우리는 F = {(r1, r2) | r1 ∈ F1 또는 r2 ∈ F2}처럼 쓸 수 있다.
-
그러므로 M은 (Q1 x Q2, Σ, (δ1(r1, a), δ2(r2, a)), (q1, q2), {(r1, r2) | r1 ∈ F1 or r2 ∈ F2})다. 이것은 M을 M1과 M2로 표현한 것이다. M1과 M2는 둘 모두 regular language이므로, M또한 regular language다
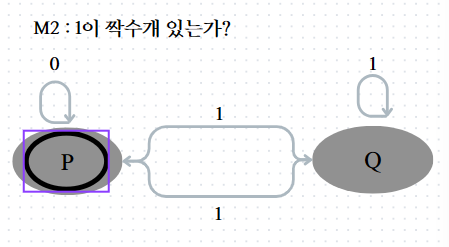
예시
다른 증명 방법
NFA를 이용하여 증명하는 방법이다.
-
language A1과 A2가 있으며, A1 ∪ A2를 할 수 있다.
-
A1과 A2를 각각 recognize하는 N1과 N2 가 있을 때, A1 ∪ A2에 대한 NFA인 N가 있다.
-
N은 N1과 N2를 가지고 있으며, 새로운 시작 지점에서 ε을 통해 각각에 접근한다. 새로 만들어진 N은 N1과 N2를 accept한다.
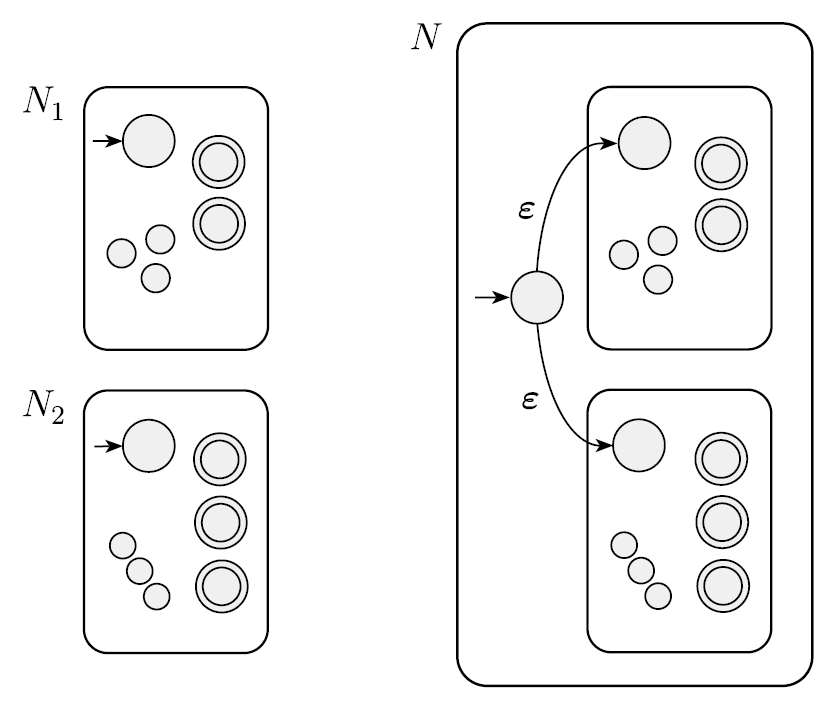
-
N1 = (Q1, Σ, δ1, q1, F1)은 A1을 recognize하고, N2 = (Q2, Σ, δ2, q2, F2)는 A2를 recognize한다.
-
새로운 N = (Q, Σ, δ, q0, F)은 A1 ∪ A2를 recognize한다.
- Q = {q0} ∪ Q1 ∪ Q2. N1과 N2의 상태들을 가지고 있으며, 새로운 시작지점 q0를 가진다,
- q0는 N의 새로운 시작지점이다.
- F = F1 ∪ F2. N의 accept state는 N1 또는 N2를 accept해야하므로 둘의 공집합이다.
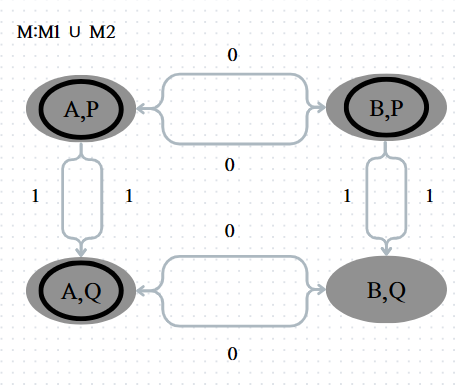
- q ∈ Q, a ∈ Σε일 때, δ은 다음과 같다.
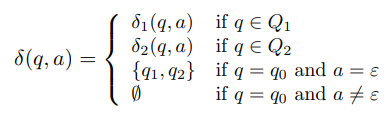
Concatenation operation
- The class of regular languages is closed under the concatenation
operation.- In other words, if A1 and A2 are regular languages then so is A1 ◦ A2.
증명 아이디어
- 앞과 같이 A1, A2를 각각 recognize하는 M1, M2가 있다고 하자.
- M은 A1 ◦ A2를 accept하는 오토마톤이다.
- 이 때, A1 ◦ A2를 앞부분 A1과 뒷부분 A2로 나눌 수 있으며, M1에 A1을 넣고, M2에 A2를 넣어 accept하는 지를 알아보면 증명할 수 있다.
- 하지만, 앞부분과 뒷부분을 어떻게 나눠야 할 지 설명할 수 없다. 예를 들어 011000010에 대해서 앞부분이 011000이고, 뒷부분이 010이면 둘 다 accpet하는 것을 알 수 있다. 하지만 앞부분이 01이고, 뒷부분이 1000010이면 둘 다 accept하지 않는 것 알 수 있다. 이처럼 나누는 곳에 따라 통과가 되는지가 달려있으며, 어디를 나눠야 할 지 우리는 알지 못한다.
- 이 문제를 해결하기 위해서는 NFA를 사용하는 것이 좋다.
증명
-
language A1과 A2가 있으며, A1 ◦ A2를 할 수 있다.
-
A1과 A2를 각각 recognize하는 N1과 N2 가 있을 때, A1 ◦ A2에 대한 NFA인 N가 있다.
-
N은 N1과 N2를 가지고 있으며, N1의 통과 상태에서 N2의 시작 상태로 ε를 이용해서 연결해 준 후, N1의 통과 상태를 그냥 상태로 바꿔준다.
-
위 과정을 통해 N의 통과상태들은 N2의 통과상태만 가지게 된다.
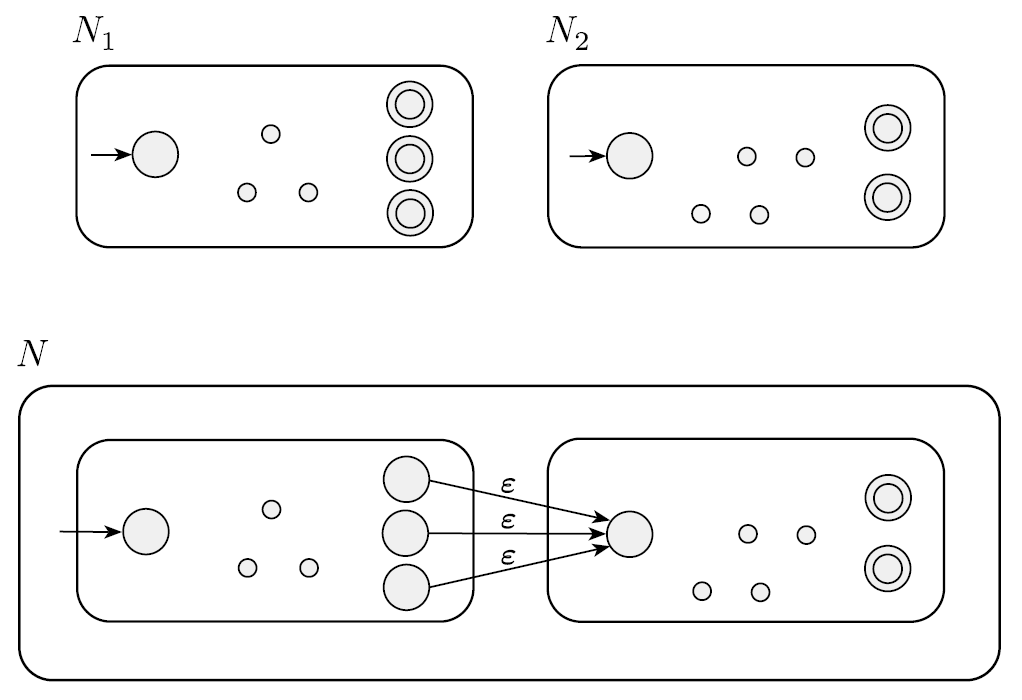
-
N1 = (Q1, Σ, δ1, q1, F1)은 A1을 recognize하고, N2 = (Q2, Σ, δ2, q2, F2)는 A2를 recognize한다.
-
새로운 N = (Q, Σ, δ, q0, F)은 A1 ∪ A2를 recognize한다.
- Q = Q1 ∪ Q2. N1과 N2의 상태들을 가지고 있다.
- q1는 N의 시작지점이다.
- F = F2. N의 accept state는 N2의 accept state랑 동일하다.
- q ∈ Q, a ∈ Σε일 때, δ은 다음과 같다.
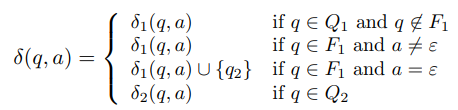
Star operation
- The class of regular languages is closed under the star operation.
- In other words, if A1 is regular language then so is A1*.
증명
-
language A1가 있으며, A1*를 할 수 있다.
-
A1를 recognize하는 N1이 있을 때, A1*에 대한 NFA인 N가 있다.
-
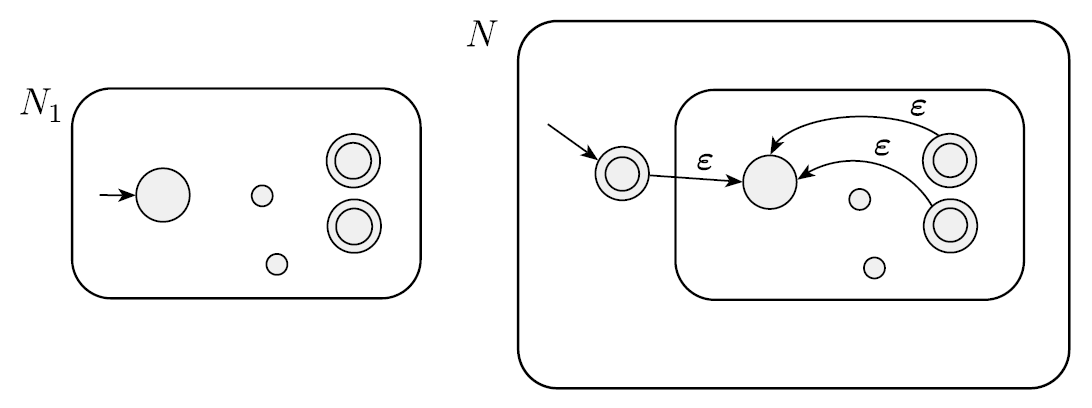
N은 N1을 가지고 있으며, N1의 통과 상태에서 N1의 시작 상태로 ε를 이용해서 연결해주면 된다.
-
이 때, 한번도 추가하지 않은 empty string 상태에 대해서도 accept해주기 위해서 새로운 시작 상태 q0를 만들어주고, 통과 상태로 만들면 된다.
-
N1 = (Q1, Σ, δ1, q1, F1)은 A1을 recognize한다.
-
새로운 N = (Q, Σ, δ, q0, F)은 A1*를 recognize한다.
- Q = {q0} ∪ Q1. N1의 상태들을 가지고 있으며, 새로운 시작지점 q0를 가진다.
- q0는 N의 시작지점이다.
- F = {q0} ∪ F1. A1*의 ε를 accept해주기 위해서 새로운 시작상태 또한 통과 상태로 가져야 한다.
- q ∈ Q, a ∈ Σε일 때, δ은 다음과 같다.