NFA(Nondeterministic Finite Automaton)

Nondeterminism

Nondeterminism은 컴퓨테이션 이론의 중요하고 강력한 개념이다.
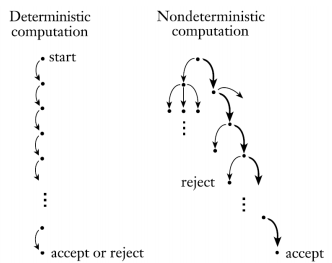
machine이 어떠한 상태(state)에 있고, 다음 symbol을 읽을 때, 다음 상태가 특정한 상태로 결정(determined)된다. 이런 개념을 deterministic computation이라고 한다.

이와 다르게, 특정한 상태에서 여러 상태로 갈 수 있는 것을 nondeterminism이라고 하며, 다음 상태가 정확히 정해지지 않았기 때문에 비결정성이라고 한다.

NFA

우리가 지금까지 배운 것은 모두 DFA(Deterministic Finite Automaton)에 대한 내용이다. 우리가 지금부터 배울 것은 NFA(Nondeterministic Finite Automaton)에 대한 내용이다.

NFA의 성질

• DFA에서는 모든 상태에서 딱 하나의 exiting transition arrow(나가는 상태 변화)가 있었다. 그러나 NFA는 여러개가 가능하다
• 아래 예시에서 q1은 0에 대해서 exiting transition arrow가 1개가 있지만, 1에 대해서는 2개가 있다.
• q2는 1에 대해서 exiting transition arrow가 없다.
• NFA에서는 exiting arrow가 한 개, 여러개, 심지어 없어도 된다.
• 또한 NFA는 alphabet안의 단어들과 ε에 대해서도 arrow를 만들 수 있다.
• 같은 symbol에 대해서 arrow가 여러개 일 수 있다.
  

NFA가 하는 일

• NFA는 string을 입력으로 받은 후, 다수의 길(multiple ways)을 실행한다
• 예를 들면, q1상태에서 다음 심볼이 1일 때, 모든 가능성에 대해서 다중적으로 실행한다.
• 그 후, 다음 심볼에 대해 두 가지로 나뉜다.
  • 만약 다음 심볼에 대해 매칭되는 arrow가 없다면, machine은 죽는다(die).
  • 만약 다음 심볼에 대해 매칭되는 arrow가 있다면, 모든 arrow에 대해서 실행한다.
• 모든 길에 대해서 하나라도 accept state에서 멈추면, NFA는 input string을 accpet한다.
• 만약 symbol이 ε면, 매칭되는 arrow가 있는지 살펴본 후, 모든 arrow에 대해서 실행한다.

예시

이 그림에 010110을 넣는 예시이다.

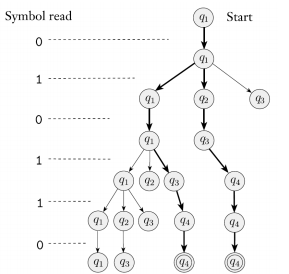
• q2상태에 ε에 대한 arrow가 있는 것을 알고 있어야 한다.
• q4는 accept state고, q4까지 간게 존재하므로 N1은 010110을 accept한다.
• 만약 N1에 010을 넣으면 어떻게 될까? 결과가 q1 아니면 q3밖에 없으므로 accept하지 않을 것이다.
• 이 예시를 통해, 11 또는 101을 포함하면 accept하는 걸 알 수 있다.

---

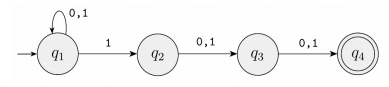
-예시를 아무거나 넣어본다. 01100 같은거...
-넣어보니 100이나 110이면 성립한다
-더 자세히 보니 string 안의 symbol이 3개 이상이고 끝에서 3번째가 1이면 accept한다.
-그러므로, 끝에서 3번째가 1인 모든 string을 accept한다.

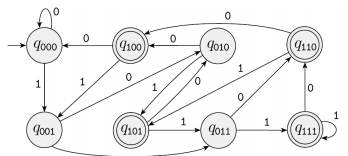
우리가 이 예시를 DFA로 그리려면 아래처럼 복잡하게 나온다. 모든 NFA는 DFA로 바꿀 수 있지만, DFA가 훨씬 복잡할 때가 있으므로 NFA로 나타내는 게 더 좋을 때가 많다.

Formal Definition of a NFA

NFA의 Formal Definition은 DFA의 Formal Definition과 비슷하다. 하지만, transirion function(δ)이 좀 다르다. DFA에선 입력과 상태를 통해 다음 상태를 결정하지만, NFA에서는 입력에 empty string도 포함이고, 이를 통해 다음 상태를 만들어내는 것이 아닌 새로운 가능성을 제공한다. 이 가능성을 상태들의 집합으로 볼 수 있다.

그러므로 Q라는 상태들의 집합이 있을 때, P(Q)는 Q의 power set(부분 집합을 모아둔 집합)이며, δ : Q × Σε → P(Q)로 정의된다.

Nondeterministic finite automaton은 5-tuple (Q, Σ, δ, q0, F)로 정의할 수 있다.
1. Q는 상태들의 집합이다.
2. Σ는 알파벳(심볼들의 집합)이다.
3. δ : Q × Σε → P(Q)
4. q0 ∈ Q는 시작 상태다.
5. F ⊆ Q는 통과상태다.

N = (Q, Σ, δ, q0, F)인 NFA이고, Σ에서 나온 string w가 있다. w = y1y2...ym이고, yi는
Σε의 memeber이며, 상태들 r0,r1,...rm이 있을 때, 아래가 성립하면 N은 w를 accept한다.

1. r0 = q0
2. ri+1 ∈ δ(ri, yi+1), for i = 0, . . . , m − 1, and
3. rm ∈ F.

• DFA때는 =이었던게, ∈로 바뀌었는데, 이는 δ가 집합이기 때문이다.

Example

N1은 (Q, Σ, δ, q1, F)다.
1. Q = {q1, q2, q3, q4}
2. Σ = {0,1}
3.

	ε	0	1
q1	∅	{q1}	{q1,q2}
q2	{q3}	{q3}	∅
q3	∅	∅	{q4}
q4	∅	{q4}	{q4}

4. 시작상태는 q1
5. q4 ⊆ F

---

NFA와 DFA는 사실 같다

우리가 지금까지 한 것을 보면, NFA는 DFA의 상위 개념인 것 같다. 하지만 NFA은 사실 DFA와 같다. NFA로 나타낼 수 있는 것들은 DFA로 나타낼 수 있으며, 반대도 마찬가지다. 이 개념이 중요한 건, 어떤 language를 나타낼 때, DFA로 그리기 어려울 때가 있다. 그럴 때 NFA로 나타내면 훨씬 간편하게 그려질 때가 있다. 이 때 중요한건, NFA == DFA려면 같은 language를 recognize해야 한다.

NFA는 똑같은 일을 하는 DFA가 존재한다.

증명 아이디어

• NFA가 language를 recognize하면, 이 language를 recognize하는 다른 DFA가 필수적으로 존재하는 것을 증명해야한다.
• NFA가 주어지면 똑같은 일을 하는 DFA로 바꾼다. 이 때, NFA와 바꾸는 과정을 simulate(동시에)한다.
• NFA에서 입력을 받아 상태로 가는 것은 가능성이라고 말했다. 그리고 가능성이라는 건 상태들의 집합이라고 할 수도 있다. 이처럼 DFA로 바꾸는 과정에서 상태들의 집합을 따라가고, 마지막에 하나의 accept state만 있으면 바꿀 수 있다.
• 이걸 하려면 먼저 가능한 조합이 얼마나 있는지를 봐야한다.
• 만약 NFA에 k개의 상태가 있으면, 2^k개 부분집합이 나올 수 있다.
• 그러므로 NFA에 k개의 상태가 있으면, DFA에는 2^k개의 상태가 나올 수 있다.
• 이제 시작상태와 통과상태를 나타내고, 똑같은지 확인하면 된다.

증명

• N = (Q, Σ, δ, q0, F)인 N이 있으며, A라는 lauguage를 recognize한다고 하자.
• 같은 언어 A를 공유하며, 같은 일을 하는 M = (Q', Σ, δ', q0', F')이 있다고 하자.
• 모든 과정을 하기 전에, empty set인 ε가 없는 N에 대해서 먼저 생각을 해보자.

1. Q' = P(Q)이다. M의 모든 상태는 N의 부분집합이며, P(Q)는 Q의 부분집합들의 합이다.
2. R ∈ Q' 이고, a ∈ Σ일때, δ′(R, a) = {q ∈ Q | q ∈ δ(r, a) ∈ R}.
3. q'0 = {q0}. M의 시작 상태는 N의 시작상태의 집합이다.
4. F' = {R ∈ Q′| R은 N의 통과상태를 가지고 있다.}.

2번의 자세한 설명

R ∈ Q' 이고, a ∈ Σ일때, δ′(R, a) = {q ∈ Q | q ∈ δ(r, a) ∈ R}다. 이것의 다른 표현은 δ′(R, a) = Ur∈R δ(r, a)다.
R상태에서 a를 만났을 때 다음 상태는 q이며, q는 a를 통해서 갈 수 있는 모든 상태들 중 하나이다.

• 이제 empty set인 ε가 있는 N에 대해서 생각해보자. DFA의 상태 R이 있으면, 여기에 E(R)을 해보자. E(R)의 뜻은 R 자기 자신과 ε을 통해서만 갈 수 있는 것들의 합집합이다. 다시 말하면, R ⊆ Q 이고, E(R) = {q | q는 R로부터 도달할 수 있는 상태들과 ε를 통해서만 갈 수 있는 것들의 합집합}이라고 할 수 있다.
• 이를 통해 우리는 DFA인 M을 ε을 고려하여 말할 수 있다.
• δ′(R, a) = {q ∈ Q | q ∈ E(δ(r, a)), r ∈ R}
• 마지막으로, M의 시작 상태 q0' 또한 E(q0)를 해야한다.

그러므로 N = (Q, Σ, δ, q0, F)일 때, M = (Q', Σ, δ', q0', F')이며

1. Q' = P(Q)
2. Σ는 공유
3. δ′(R, a) = {q ∈ Q | q ∈ E(δ(r, a)), r ∈ R}
4. q0' = E(q0)
5. F' = {R ∈ Q}

라고 말할 수 있다.

NFA는 DFA로 바꿀 수 있다.

어떤 NFA가 language를 recognize하면 그 language는 regular이며, 반대도 가능하다.
→: regular language는 특정한 DFA를 recognize하며, 모든 DFA는 NFA로 바꿀 수 있다.
←: NFA가 어떠한 language를 recognize하면, 그 language를 recognize하는 DFA가 있으며 같은 langauge는 regular language다.

---

NFA와 DFA의 단순화

NFA나 DFA 모두 특정한 language L에 대해서 여러가지가 있을 수 있다. 그러나 state가 가장 적은 automaton이 language에 대해서 잘 나타내며, state를 줄이는 과정을 단순화(minimalize) 라고 부른다

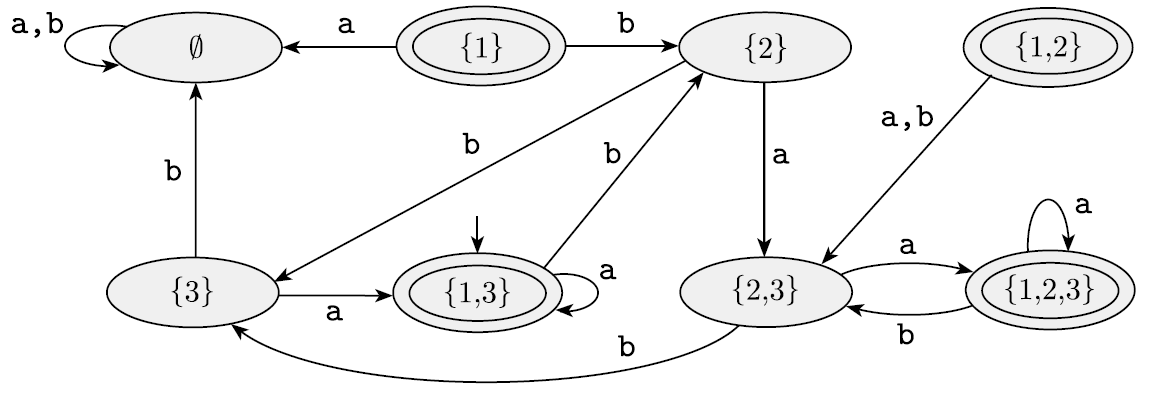
다음과 같은 예시가 있을 때, 상태 {1}, {1,2}로 접근할 수 있는 arrow가 없다. 그러므로 사실상 없는 상태와 같다. 이 없는 상태와 그로부터 파생되는 arrow들은 쓸모가 없으므로 없앨 수 있다.

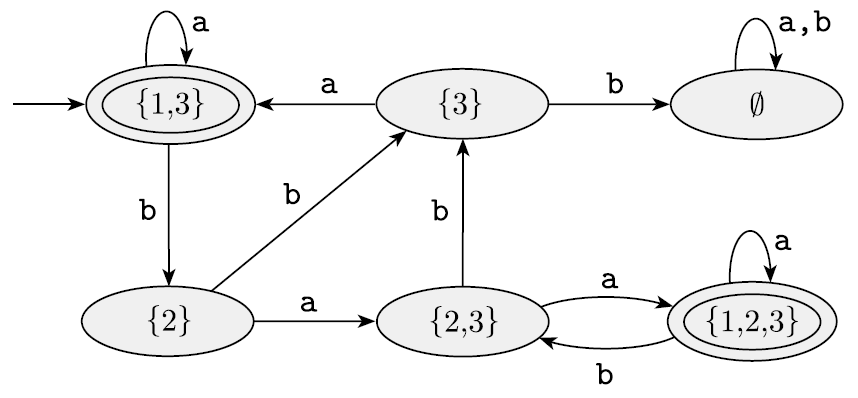
상태를 없앤 그림이다. 위 그림과 아래 그림은 기능적으로 같으며, 똑같이 L을 recognize한다.