Time Complexity in Computation Theory
- 어떤 문제가 decidable하다고 해보자. decidable하면 결국에는 풀 수 있다.
- 근데, 문제가 decidable해도 오래 걸리면 사실상 못 푸는 문제이다.
- 공학과 과학의 차이인데, 이론적으로 풀리는 문제여도 실제 푸는데 오래 걸리면, 사실상 풀기 힘든 문제이다.
- 주의해야 할 것이 있는데, 우리가 관성적으로 나타내는 표기법은 알고리즘의 시간 복잡도를 나타내는 것이다.
- 정렬 알고리즘은 등등 나타낼 수 있다. 어떤 알고리즘은 빠르며, 어떤 알고리즘은 느리다.
- 그러나 여기서 나타내는 시간 복잡도는 문제에 대한 얘기이다. 정렬 문에 대한 시간복잡도는 이라고 규명할 수 있으며, 라고 말하면 틀린 것이다.
Measuring Complexity
를 만족하는 함수,가 있다고 하자.
양의 정수 와 이 있고, 이면 로 나타낸다.
로 나타냈을 때, 은 적어도 보다는 커야 한다.
은 인 함수라고 해보자.
제일 높은 차수인 and 을 생각해보면, 이라고 할 수 있다. (5를 곱하는 건 고려하지 않는다. 임의의 양의 정수 c가 5보다 크면 성립하기 때문.)
비슷하게, 으로 나타낼 수 있는데, 가 보다 크기 때문이다. 하지만 실제로 쓸모는 별로 없다.
그러나, 는 안된다. 왜냐하면 실제로는 이것보다 오래 걸리기 때문이다.
인 함수 이 있다고 하자.
multitape Turing machine이 을 수행할 때 동일한 일을 수행하는 single-tape Turing machine은 만큼 걸린다.
- multitape turing machine은 tape와 head가 여러개가 있으며 한번에 움직인다.
- 이것을 따라하는 single-tape turing machine은 모든 tape의 내용을 한 tape에 기록한다.
- multitape turing machine이 한번의 작업을 할 때, 최대 tape 길이만큼 작업을 할 것이다.
- multitape turing machine이 한번 작업 할 때 한칸만 늘어나므로, 만큼 작업하면 길이는 만큼 더 늘어날 수 있다.
- 그러므로 한번 작업에 걸리는 최대 시간은 이고, 이것을 번 작업하므로, 만큼 걸린다.
Nondeterministic Single-Tape Turing Machine
Let be a nondeterministic Turing machine that is a decider.
The running time of is the function , where is the
maximum number of steps that N uses on any branch of its computation on any input of length n, as shown in the following figure.
은 nondeterministic single-tape Turing machine이 어떠한 일을 수행하는 함수이며, 일때, 동일한 일을 하는 deterministic single-tape Turing machine은 만큼 시간이 걸린다.
- Leaf로 가는 경우를 생각해보자
- Turing Machine에서 제일 많이 분기가 생기는 경우에 분기의 개수를 라고 하자.
- Root에서 한 번 진행했을 때 Node 개수는 이다.
- 그러므로 길이가 일때 Leaf 개수는 개이다.
- 한번 Leaf로 갈 때 이 걸리므로, 모든 작업을 수행하는 시간은 이다.
The Class P
- signal tape과 multitape은 다항식과 제곱함수의 차이이다.
- determintic single-tape과 nondeterministic single-tape은 다항식과 지수함수의 차이이다.
- 이 둘은 큰 차이가 있으며 polynomail difference와 exponential difference사이에는 많은 차이가 있다.
- deterministic computational model은 polynomial difference하다.
는 decidable(solvable)하며, deterministic single-tape으로 polynomial time에 풀 수 있는 language들의 집합이다.
이며, 이다.
- P는 문제들의 집합이다. 원래 문제들의 집합은 문제를 푸는 computational model이 달라지면 달라져야 하지만, P는 바뀌지 않는다.
- P는 무조건 deterministic signle-tape Turing machine으로 polynomial한 시간에 풀 수 있는 문제들의 집합이다.
- P는 실제로 현대 컴퓨터에서 우리가 풀 수 있는 문제들의 집합이라 할 수 있다.
Example of P : Path Problem
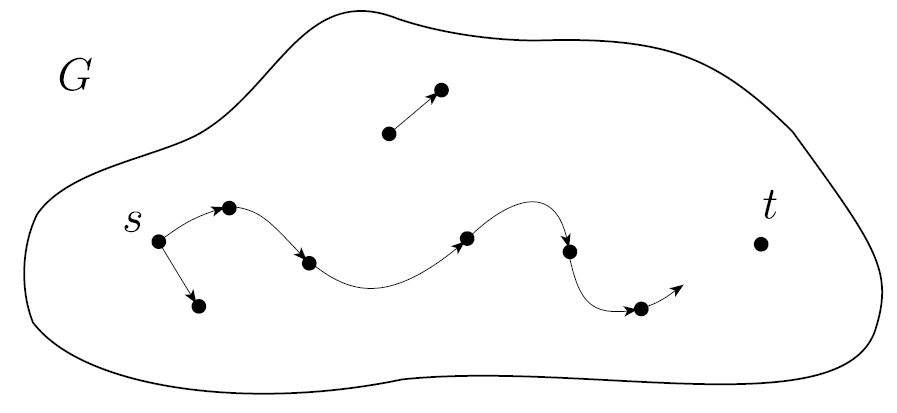
- 방향 그래프 G는 어떤 노드 s와 t를 가지고 있다.
- s에서 t로 가는 PATH가 있는 지 확인하는 것이 Path Problem이다.
- 는 무방향 그래프이며 에서 로 가는 PATH가 있다.
- 가장 간단한 방법을 보자。
- 일 때, m개 Node가 순서대로 들어갈 수 있는 배열이 있다.
- 각각에 첫번째 노드부터 마지막 노드까지 순차적으로 넣어본다.
- 만약 t로 갈 수 있을 때, Edge가 있으면 PATH는 accept한다.
- 그러나 이렇게 되면 실제 시간은 exponential 시간이다.
- s의 근접 노드를 표시한다.
- 표시한 노드 중 t가 있으면, accept한다.
- 표시한 노드 중 t가 없으면, 모든 표시한 노드의 근접 노드를 다시 표시한다.
- 만약 모든 근접 노드가 표시한 노드이면, reject한다.
- 노드가 m개 있으면, m*m에 끝난다.
- 실제로는 더 빠름
- 그러므로 에 끝나므로 PATH문제는 P문제 안에 들어간다고 할 수 있다.
Example of CFL : CFL ⊆ P
- 일단, CFL은 decidable하다.
- CFL이 decidable한 것을 증명할 때, Chomsky normal form으로 바꾸어서 증명했다.
- 이 때, 만큼 진행했을 때 가 나오면 accept하고, 아니면 reject한다.
- 문제가 있는데, 만큼 진행했을 때 Leaf의 개수는 이다. 이러면 exponentail time이므로 P문제가 아니다. 이 되기 때문이다.
- 여기서 전 상태를 저장하는 DP 방법을 사용하면 인 문제로 바꿀 수 있다. 증명할 수 있지만 여백이 없어서 생략한다.
- 그러므로 인 문제이므로 모든 이다.
The Class NP
- 우리는 여러가지 알고리즘과 방법을 통해 여러 문제들을 polynomial time solution으로 바꿀 수 있다.
- 그러나, 모든 문제를 polynomial time solution으로 바꿀 수 있는지는 아직 알지 못한다.
- 이게 무슨 말이냐면, 모든 문제가 P인지를 증명 못했다는 것이다.
- 그렇다고 P로 바꿀 수 없는 NP인 문제가 있을 수 있다는 것도 증명하지 못했다.
- 모든 문제가 P인지, NP문제가 있는지 알 수 있는지, 없는지도 증명하지 못했다.
Hamiltonian path
- Hamiltonian path는 방향 그래프 가 있고, 각 노드를 한번씩만 가는 path이다.
- 는 방향그래프이며, 에서 로 가는 Hamiltonian path이다.
- HAMPATH가 polynomial time에 풀리는지는 아무도 알지 못한다.
- 예를 들어보자. 위에서 본 방법으로 풀 수도 있다.
- 그러나 그 방법은 이 걸린다.
- 그러므로 exponential time이며, polynomial time에 풀리는지는 증명되지 않았다.
P vs NP
는 deterministic single-tape Turing machine으로 polynomial time에 decidable(solvable)할 수 있는 language들의 집합이다.
는 verifier가 있어서 polynomial time에 decidable(solvable)할 수 있는 language들의 집합이다.
는 nondeterministic Turing machine으로 polynomial time에 decidable(solvable)할 수 있는 language들의 집합이다. 역도 같다.
Polynomial Verifiablity
- 현재로써 HAMPATH 문제를 polynomial verifiability할 수 있는, 다시 말해 polynomial time에 푸는 정형화된 방법은 없다.
- 그러나 어떤 예시를 주었을 때, 그 예시가 답인지 답이 아닌지를 확인하는 것은 polynomial time에 할 수 있다.
- 이것이 verifiable이다.
- 답의 후보가 주어졌을 때, 그 후보가 답인지 아닌지를 확인하는 것을 verifiable이라고 한다.
- 다른 verifiable의 예시는 합성수인지 확인하는 게 있다.
- 어떤 자연수가 있을 때, 그 자연수가 합성수인지는 polynomial time에 가능하지 않다.
- 그러나 자연수를 구성할 거 같은 두 자연수를 주면, 합성수인지는 polynomial time에 판별할 수 있다.
- 에를 들어, 5,183이라는 정수가 있다.
- 합성수는 임의의 상수
- 이게 합성수인지는 2부터 5,183까지 수를 곱해가면서 5183이 나오는지를 확인해야 한다.
- 물론 여기서 5,183이 넘어가면, 더 큰 수를 곱해도 소용 없으므로 다음으로 넘어가도 된다.
- 그러나 이렇게 해도 대충 이 된다.
- 만약 71, 73이라는 답 후보를 준다면 어떻게 될까? 71*73 = 5,183이므로 합성수임을 쉽게 알아낼 수 있다.
- 이처럼 특정한 답 후보를 주었을 때 그것을 가지고 Polynomail time 안에 풀 수 있으면, Polynomial verification하다.
- 그러나 HAMPATH가 없다는 것을 밝혀내는 건 polnomial time에 불가능하다.
- 답이 아닌 예시를 주어도, 그것이 HAMPATH가 없다는 것을 반증하지는 않는다.
- 그러므로 HAMPATH가 없다는 것을 증명하려면, 모든 답이 아닌 경우에 대해서 해보아야 한다.
- 이것은 모든 과정을 다 하는 것과 비슷하므로, polinomail time에 불가능하다.
language 에 대한 알고리즘 는 는 어떤 string 에 대해서 를 accept한다
라는 예시가 있으면, polynomial time 안에 가 안에 들어가는지를 확인한다.
여기서 는 polynomial time verifier이며, 는 certificate 라고 한다.
는 polynomial time verifier를 가지고 있는 language이다.
- 이에 따르면, nondeterministic Turing machine (NTM)이 HAMPATH를 polynomial time에 풀 수 있다.
- 는 방향그래프이며, 와 는 노드이다.
- 까지 노드가 들어가는 배열을 만든다. m은 G의 노드 개수이다.
- 같은 노드가 나오면, reject한다.
- 이고 이여야 한다. 아니면 reject한다.
- 부터 까지 볼 때, 임의의 에 대해서 와 를 잇는 edge가 모두 있으면 accept하고, 아니면 reject한다.
은 nondeterministic Turing machine이 시간 안에 풀 수 있는 language들의 set이다.
Clique
- Clique는 무방향 그래프의 subgraph이며, Clique 안에 있는 어떤 두 노드를 뽑아도 둘을 연결하는 edge가 있는 subgraph이다.
- k-Clique는 k개의 node를 가진 그래프이다.
- 는 무방향 그래프이며 k-clique를 가지고 있다.
- 이 문제는 NP이다. NP이려면 verifier가 있거나 polynomial nondeterministic turing machine이 있으면 된다.
- CLIQUE의 verifier를 라고 하자.
- 에 대해서 다음과 같이 동작한다.
- 가 의 k개의 노드를 가진 subgraph가 아니면, reject한다.
- 각각의 node를 연결하는 모든 edge가 있는지 확인한다.
- 있으면 accept하며, 없으면 reject한다.
- 다른 증명 방법으론 nondeterministic turing machine으로 한다.
- 에 대해서 다음과 같이 동작한다.
- Nondeterministic하게 에서 개의 노드를 가지는 subgraph 를 선택한다.
- 각각의 node를 연결하는 모든 edge가 있는지 확인한다.
- 있으면 accept하며, 없으면 reject한다.
P vs NP 문제
- P라는 클래스의 문제들이 있다. 이 문제들을 DTM으로 polynomial time안에 풀 수 있다.
- NP라는 클래스의 문제들이 있다. 이 문제들을 NTM으로 polynomial time안에 풀 수 있다.
- 그렇다면 둘의 관계는 어떻게 될까?
- P와 NP는 완전히 다른 문제이다.(같은 게 없음)
- P와 NP는 교집합이 있으나, 포함관계는 아니다.(같은 게 있으나, 포함하거나 동일하지 않음)
- P가 NP를 포함한다.
- NP가 P를 포함한다.
- P와 NP는 같다.
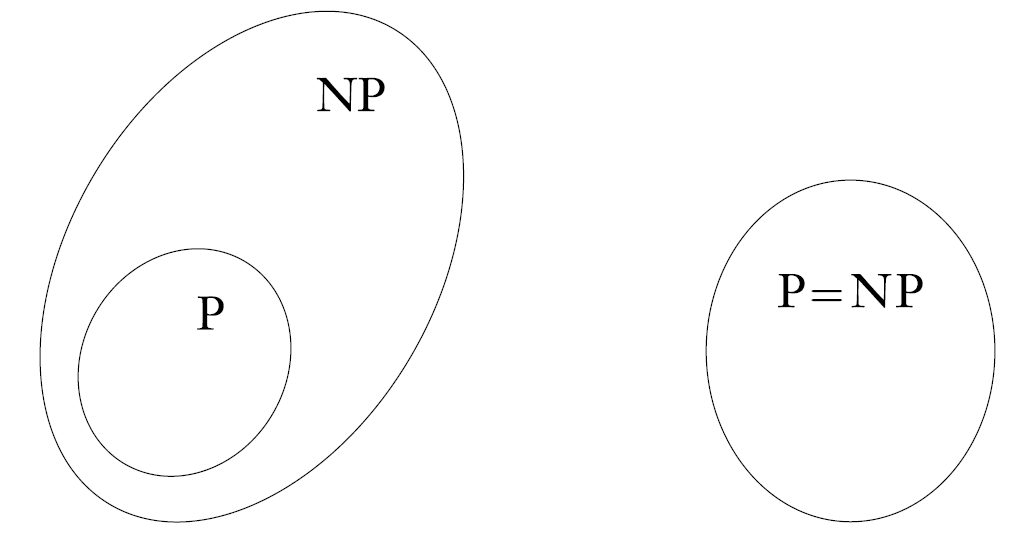
- DTM은 자동으로 NTM이다. 그러므로 교집합이 없을 순 없다.
- 그러므로 1,2,3번은 안되므로 4,5번 중 하나이다.
- 만약 NP문제를 푸는 DTM이 있다면 P와 NP는 같다.
- 그러나 이런 DTM이 있는지는 아직까지 알려지지 않았다...
NP-Completeness
- P와 NP의 관계는 잠시 내버려두자.
- NP안에 있는 문제 중, 특정한 문제는 가장 어려운 문제인 것 같다.
- 그러므로 특정한 문제를 풀면, 나머지 문제를 전부 풀 수 있을 것 같다.
- NP문제 중에서 polynomial time 안에 풀 수 있으면, 모든 NP 문제를 풀 수 있는 문제를 NP-complete라고 한다.
- P ≠ NP를 증명하고 싶으면, NP-Complete 문제를 통해 증명하면 된다. 왜냐하면 NP문제중 제일 어려운 문제이기 때문이다.
- P = NP를 증명하고 싶으면, NP-Complete 문제를 통해 증명하면 된다. 왜냐하면 NP문제가 풀리면 나머지 문제 또한 모두 풀리기 때문이다.
- 그러므로 P vs NP 문제를 풀려면 NP-Complete에 대해서 분석하면 된다.
SAT
- 어떤 Boolean 식이 있을 때, 이 식의 값을 1로 만드는 변수들의 값을 찾아내는 문제이다.
- 예를 들어, 라는 식이 있다.
- 답 중 하나로, 이면 이 된다.
- 가 1이 되도록 하는 모든 식의 값이다.
Polynomial Time Reducibility
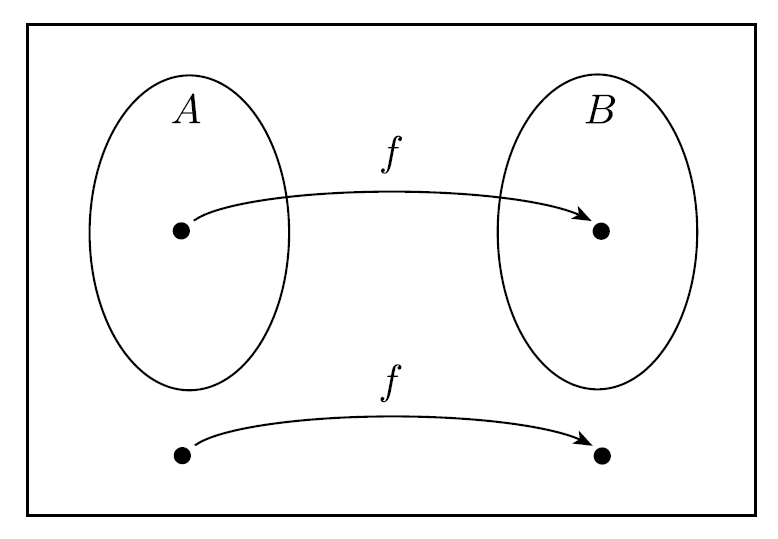
language 가 language 에 대해서 reduction을 polynomial time에 한다면, 간단히 말해 polynomial time reducible 하다면, 라고 나타낸다. B가 A보다 어려운 문제라는 의미이다.
polynomial time computable function 이 있으면, 모든 string 에 대해서, 이다.
- 만약 를 로 reduction하면, 아래와 같은 특징이 있다.
- & ,
- A를 B로 polynomial time에 바꿀 수 있고, B를 polynomial time에 풀 수 있으면, A는 B보다 쉬운 문제이므로 A 또한 polynomial time에 풀 수 있다.
- 이에 대한 반대로, A를 polynomial time에 바꿀 수 있고, A가 NP이면, B또한 NP이다.
- 왜냐하면 B는 A보다 어렵기 때문에, 자동으로 NP가 된다.
3SAT
- 3SAT은 SAT의 특별한 형식이다.
- 이진 변수 처럼 변수와 그 변수의 반대(complement)를 literal이라고 한다.
- clause는 ∨(or)로 묶인 하나의 단위체다.
- conjunctive normal form으로 구성되어 있다. clause들이 and로 묶여있다.
- 이 때 conjuctive normal form은 모든 clause들이 참이여야 하며, clause 안의 literal중 하나만 참이면 된다.
- 3cnf-formula는 cluase가 3개의 literal로 묶인 cnf를 듯한다.
- 여기서 중요한 건, 임의의 boolean fomular는 3cnf-formula로 바꿀 수 있다.
- 는 3cnf-formula를 만족한다.$}$
은 polynomial time에 로 reduciable하다.
- 이것을 증명하려면, 에서 accept하면 에서 accept해야 하고, 반대로 reject하면 똑같이 reject해야 한다.
- 인 가 있다고 하자.
- 그러면 다음과 같은 그림을 그릴 수 있다.
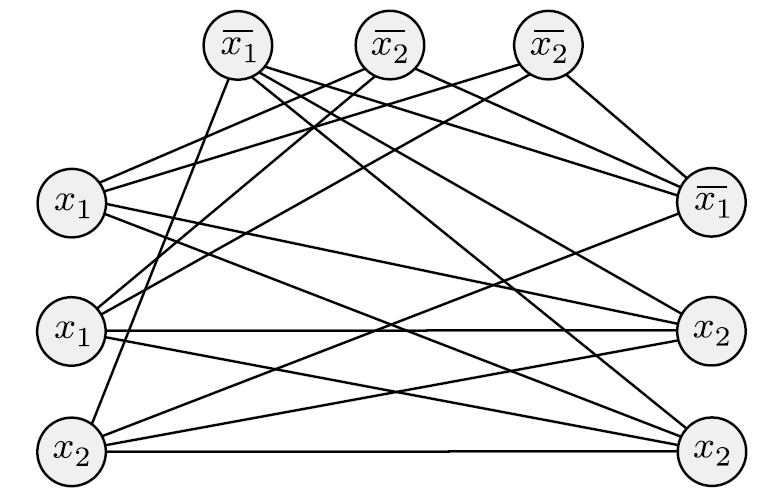
- 같은 clause 사이에는 edge가 없으며, 만약 이 있으면, 에는 edge가 없다.
Proof of 3SAT - CLIQUE
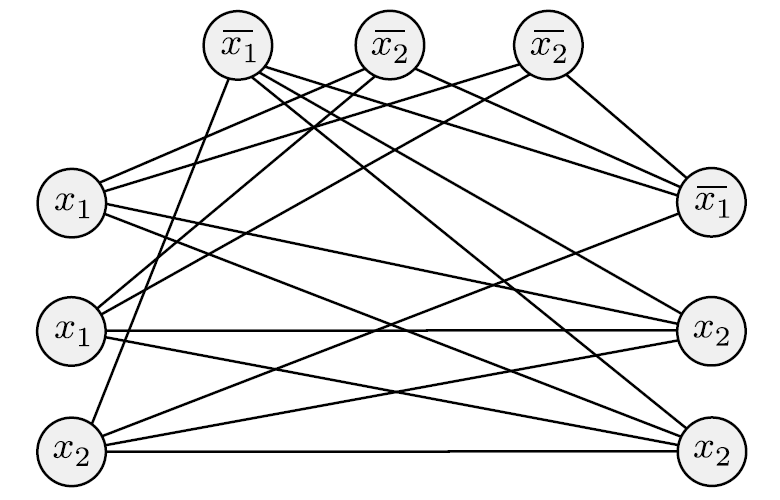
- 만약 위에서 , 이면, 식이 1이다. 이러면 답들을 표시한다.
- 답들 사이에는 무조건 edge가 있어야 하는데, 모순 관계가 되도록 표시하지는 않았기 때문이다.
- k-clique가 있으면, 답이 존재한다.
language B가 NP-complete이려면, 다음 조건을 만족해야한다.
1) B는 NP이다.
2) NP안에 있는 모든 language A는 polynomial time에 B로 reducible해야 한다.
만약 B가 NP-complete이고 이면, 이다.
만약 B가 NP-complete이고 NP인 C에 대해서 할 수 있다면, C는 NP-complete이다.
- 일단 NP-complete를 하나라도 알 수 있으면, 다른 NP문제에 대해서 complete한지 알아낼 수 있다.
- 이 하나라도 알아낸 것이 바로 SAT이다.
SAT은 NP-complete이다.
1) SAT은 NP이다.
2) NP안에 있는 모든 language A는 polynomial time에 SAT으로 reducible해야 한다.
1번의 증명 : 모든 variable에 대해서, nondeterministic하게 경우들을 만들어 본다. 그 후, 각각에 대해서 polynomial time에 풀 수 있으므로(모든 경우들에 대해서 참이 되는지 확인만 하면 된다.), SAT은 NP이다.
2번의 증명
- 임의의 NP문제는 NTM 이 존재하며, string 를 polynomial time에 accept한다.
- NP에서 SAT으로 변환 과정을 거친다. NP가 accept하면, SAT또한 accept한다. NP가 reject하면, SAT또한 reject한다.
- 로 구성된다.
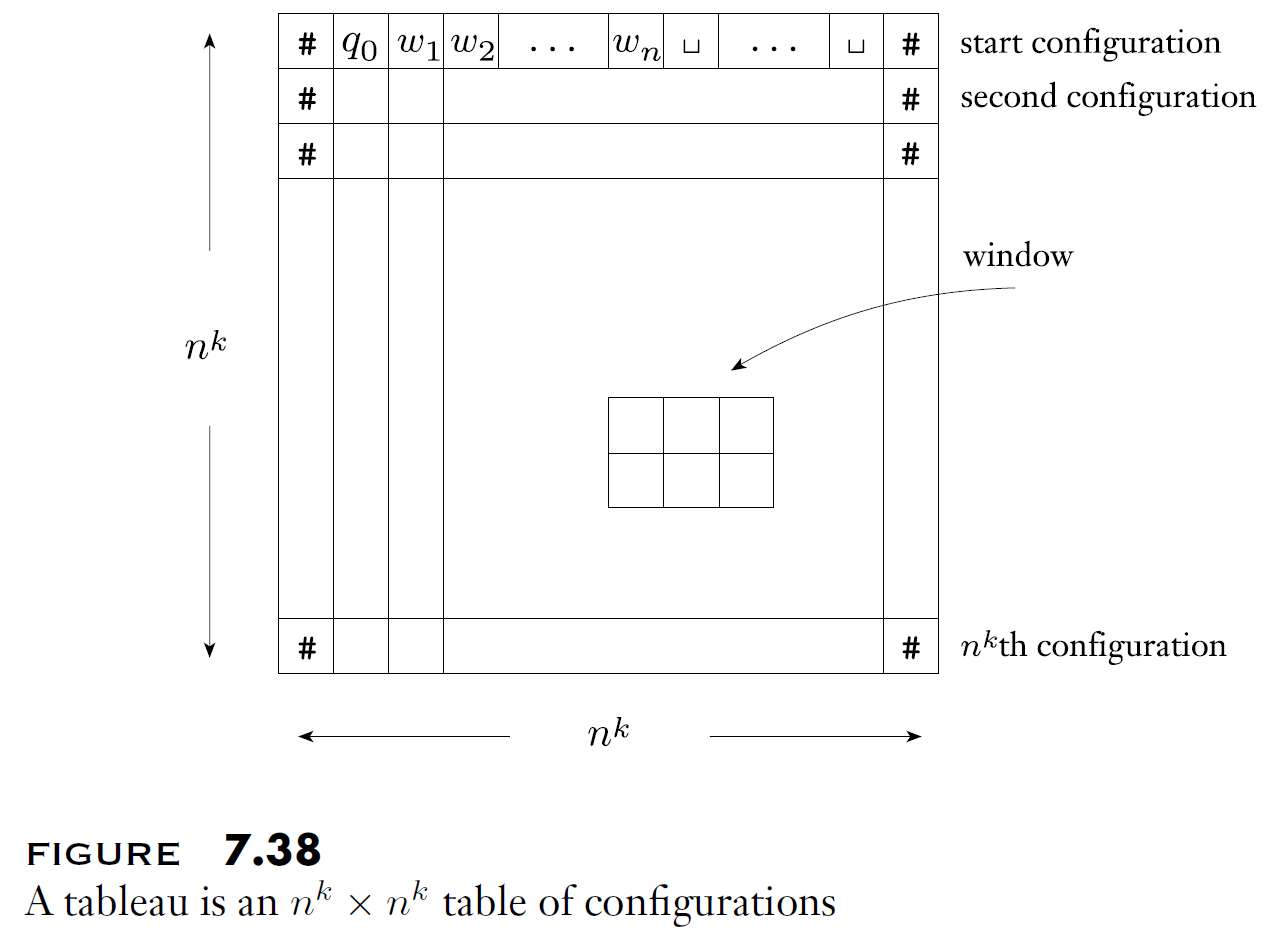
- 의 의미는, 맨 처음에 start configuration을 잘 작성해야 한다는 의미이다.
- 의 의미는, 마지막에
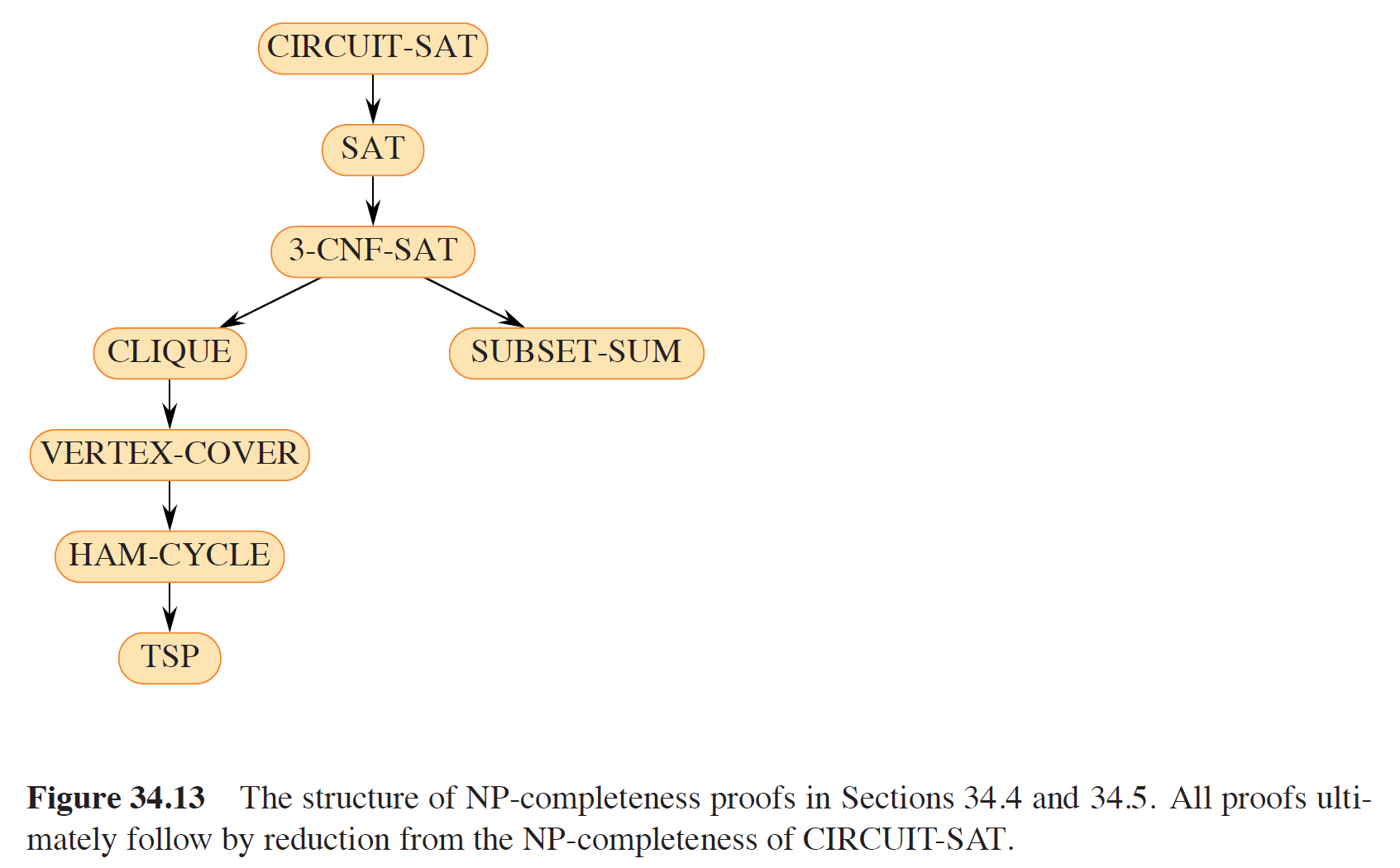
Additional NP-Complete Problems