Undecidability

Undecidability

• 어떤 language가 string을 만들 수 있는지 판별하는 TM을 통해 language들의 관계를 알 수 있었다.
• 이제 중요한 문제가 남았다. 알고리즘이 풀 수 없는 문제가 있다는 것이다.
• 알고리즘이 풀 수 없는 문제를 undecidable하다고 한다.
• undecidable은 accept / reject 하지 않는다는 의미가 아니다. halt하지 않을 수 있다는 의미이다.
• undecidable한 문제의 예시이다.
  • 누군가가 만든 어떤 정렬 프로그램이 있다.
  • 모든 경우에 대해서 정렬 프로그램이 정렬하는가?
  • 이를 알 수 없다...

General problem of Software verification

• General problem of Software verification은 컴퓨터로 풀 수 없다.
• 하지만, "그냥 풀 수 없네~ 끝!" 이렇게 하는 것도 별로 좋지 않다.
  • 만약 위처럼 되었다면 정리되어 있는 정렬 알고리즘은 모두 이상한 것이 될 것이다.
• 간단하게 설명하자면, Software verification으로 정의되어 있는 것을 Formal verification으로 변환한다. 다시 말해 문제의 범위를 줄이는 과정을 거친다.
  • 위에서의 "정렬"을 정의해보자면 "i,j가 있을 때, i > j 이면 $a_i > a_j$이다."라고 할 수 있다.(오름차순 정렬)
  • 이렇게 정의를 하면 푸는 알고리즘은 한트럭이다.

Universal Turing Machine

• 이제 우리가 지금까지 해 왔던 것을 Turing Machine단위부터 다시 할 것이다.
• language $A$가 주어지고, $A$에 해당되는 $w$가 있다.
• 어떤 Turing Machine이 주어질 때, 이 TM이 $w$를 만드는 지 판별하는 TM을 $A_{TM}$이라고 부른다.
• $A_{DFA}$나 $A_{CFG}$는 decidable하다. 그러나 $A_{TM}$은 undecidable하다.
• $A_{TM} = \{⟨M,w⟩ |M$는 TM이며 string $w$를 accept한다.$\}$

$A_{TM}$은 undecidable하다.

• 이를 증명하기 전에, $A_{TM}$이 Turing-recognizable한 것부터 증명해야 한다.
• Turing Machine $U$는 $A_{TM}$을 recognize한다.
• $U$는 $⟨M,w⟩$에 대해서 $w$를 $M$이 accept하면 accept하고, reject하면 reject한다. 또한 $w$에 대해서 $M$이 loop하면 똑같이 loop한다.
• 그러므로 $U$는 Turing-recognizalbe하다.
• 그렇다면, $M$이 loop하는지 하지 않는지. 다시 말해 halt하는지 하지 않는지를 알려주는 TM이 있다면, 문제가 해결되지 않는가?
  • 만약 halt하면, accept
  • 만약 halt하지 않으면, 다시 말해 loop하면 reject
• 하지만 이런 알고리즘은 존재하지 않는다. 이를 halting problem이라고 한다.

Turing Machine이 halting 하는지, 안하는지 알 수 있는 Turing Machine은 존재하지 않는다.

• 그러나 $U$는 그 자체로도 큰 의미가 있다.
• 입력으로 된 Turing Machine을 따라할 수 있다는 것은, 어떤 Turing Machine이든 따라할 수 있다는 것이다.
• 더 나아가자면, 지금까지 Turing Machine은 특정한 일 한가지만을 수행했다.
• $U$는 다른 모든 Turing Machine을 따라할 수 있다. 다시말해 Turing Machine이 할 수 있는 모든 일을 할 수 있다.
• 이 $U$를 Universal Turing Machine이라고 한다.
  • 만약 동영상을 보고 싶다면, 동영상을 보여주는 Turing Machine을 따라할 수 있다.
  • 만약 게임을 하고 싶다면, 게임의 동작을 수행하는 Turing Mahcine을 따라할 수 있다.
• 이는 엄청난 일으로, 지금까지 인간이 만든 도구는 한가지 일 밖에 수행하지 못했다.
• 그러나 Universal Turing Machine은 여러가지 일, 어찌 보면 엄청나게 만든 일을 수행할 수 있는 것이다.
• 이러한 이유로 인해 현대 컴퓨터는 Universal Turing Machine을 기반으로 하고 있다.

The Diagonaliztion Method

• Halting Problem을 풀 수 없는 것은 diagonalization으로 증명했다.
• Cantor는 1873년에 diagonalization을 발견했다.
• Cantor는 무한한 집합의 크기를 측정할 수 있었다.
• 만약 무한한 집합이 2개 있을 때, 두 집합의 크기를 비교할 수 있는가?

자연수와 짝수의 개수

• 무한한 짝수와 무한한 자연수의 크기는 같은가?
• 얼핏보면 자연수가 짝수보다 많은 것 같지만, 사실 무한한 자연수와 무한한 짝수의 크기는 동일하다.
• 유한한 집합은 원소의 개수를 셈으로써 크기를 비교할 수 있다.
• 무한한 집합은 어떻게 알 수 있을까?
• Cantor는 집합간에 일대일대응이 되면 두 집합의 크기가 같다고 말했다.
  • 집합 $A$와 $B$가 있다.
  • $A,B$에 대한 함수 $f$가 있다.
  • $a≠b$면 $f(a)≠f(b)$여야 한다.
  • 또한 $b∈B$이고 $a∈A$면 $f(a) = b$이다.
  • 말로 풀어서 설명하면, a와 b가 서로 하나씩만 매칭되어 있다.
• 자연수 집합 $\mathbb{N} = {1,2,3,...}$과 짝수 집합 $\mathbb{E} = {2,4,6,...}$이 있다.
• 위에 따르면 $|\mathbb{N}|=|\mathbb{E}|$다.
  • 일대응대응으로 만드는 함수 $f(n) = 2n$이 있다.
  • $1 → 2, 2 → 4, 3 → 6, ...$
  • 이 함수를 따르면, 자연수 집합의 원소 하나는 짝수 집합의 원소 하나와 대응된다.
  • 그러므로 자연수 집합과 짝수 집합의 크기는 같다.
    

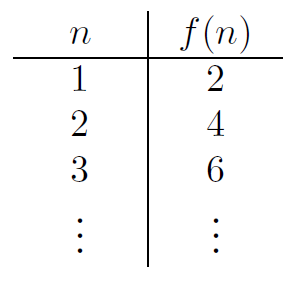
자연수의 개수와 짝수의 개수는 같다.

자연수와 유리수의 개수

• 자연수와 유리수의 개수는 같은가?
• 앞에서 자연수와 짝수의 개수가 같다고 했지만, 유리수는 소수가 들어가므로 훨씬 많아 보인다.
• 결론부터 말하면, 유리수와 소수의 개수는 같다.
• 유리수 집합은 $\mathbb{Q} = \{\frac{m}{n} | m,n ∈ \mathbb{N}\}$로 정의할 수 있다.
• 만약 둘이 같으면, $\mathbb{N}$와 $\mathbb{Q}$의 요소들을 잘 연결시킬 수 있으면 된다.
• 하나도 빠짐없이 연결되면, 둘의 크기는 같다.
• 모든 유리수에 대해서 다음과 같이 나타낼 수 있다.
  
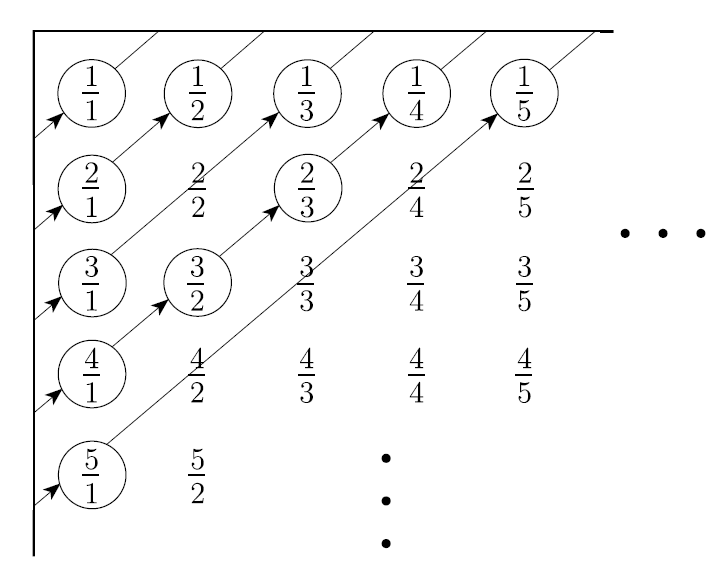
• 위쪽은 분모이며, 아래쪽은 분자이다.
• $\frac{i}{j}$는 i번째 가로와 j번째 세로에 있는 유리수이다.
• 이것에 대해서 좋지 않은 아이디어는, 그대로 가로부터 진행하는 것이다.
• 그렇게 되면 첫번째 가로부터 진행할 때 무한히 매칭되므로, 두번째로 진입하기 어려워진다.
• 대각선으로 매칭시켜보자.
  
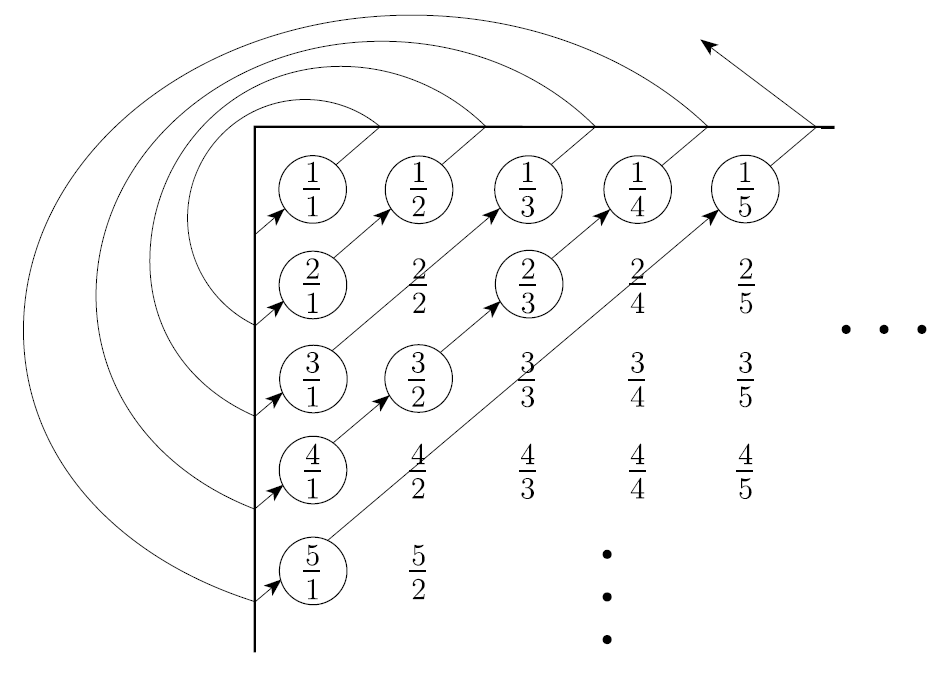
• $1 = \frac{1}{1}$, $2 = \frac{2}{1}$, $3 = \frac{1}{2}$... 이렇게 계속 매핑시켜나간다.
  • 이 때 $\frac{1}{2}$와 $\frac{2}{4}$는 같은 것이다. 약분이 되므로 다시 매핑하지 않는다.
• 이것을 반복하면 모든 유리수와 자연수를 매핑시킬 수 있다.

유리수의 개수와 짝수의 개수는 같다.

Real Number

• 자연수와 유리수 개수의 비교를 통해서 동일한 크기의 무한 집합을 알 수 있었다.
• 그러나 동일하지 않은 크기의 무한 집합또한 있다.
• 무리수(실수)의 개수는 자연수의 개수와 동일하지 않다.

  $R$은 uncountable이다.

• $\mathbb{N} \overset{f}→ \mathbb{R}$면 $\mathbb{N}$과 $\mathbb{R}$의 개수는 동일하다.
• $\mathbb{R}$에서 임의의 x들을 뽑아서 $\mathbb{N}$과 pair시킨다.
• 
• x는 f(n)의 n번째 숫자+1을 모은 실수이다.
  • 예를 들어, 0~1 사이의 실수 x를 뽑아보자.
  • 이 x는 f(1)의 소수점 첫번째 자리보다 1 높은 숫자이다.
  • 또한 x는 f(2)의 소수점 두번째 자리보다 1 높은 숫자이다.
  • 만약 f(n)이 9면, x의 n번째 자리는 0이다.
  • 이렇게 계속 간다...
  • $x = 0.2641...$
  • 이렇게 되면 x는 f(n)과 다른 모든 자리수가 맞아도, 소수점 n번째 자리수가 항상 다르므로 pair할 수 없다.
    
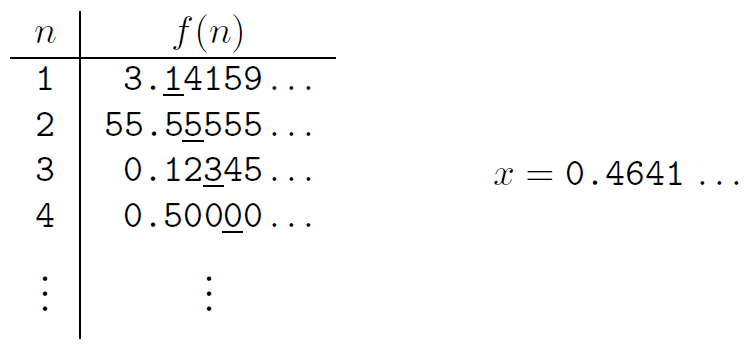
  • 이러면 n과 f(n)은 일대일 대응이 아니므로, $\mathbb{N}$과 $\mathbb{R}$은 일대일 대응이 아니다. 그러므로 자연수와 실수는 개수가 동일하지 않다.
  • 또한, 실수는 자연수보다 개수가 많다.

Diagonalization Method in Turing Machine

• 이처럼 무한의 개수는 다를 수 있다.
• 이것을 Language와 Turing Machine에 적용해 볼 수 있다.
• 결론부터 말하면, TM으로 나타낼 수 없는 Language가 있으며, Language의 개수가 더 많다.

Some languages are not Turing-recognizable

• Turing machine이 countable하다는 것을 보이기 위해, $Σ^{*}$이 countable함을 먼저 보인다.
• $Σ^*$의 가지수는 countable하다.
  • 예를 들어, $Σ = {0,1}$일 때, $Σ^* = {,0,1,00,01,10,11,000,..., }$으로 나타낼 수 있다.
  • 다시 말해 symbol로 만든 모든 string의 집합이다.
  • $Σ^*$은 자연수에 하나하나 대응할 수 있다.
  • 여기서 Turing machine은 countable하다. 각각의 TM $M$은 string $⟨M⟩$으로 표현되어 $Σ^*$안에 포함 될 것이다. 그러므로 모든 TM은 $Σ^*$안에 포함될 것이다.
• 이제 language의 개수를 세보자.
• 결론부터 말하면, language의 개수는 uncountable하다.
• 이를 증명하기 위해, 끝나지 않는 string을 본다.
  • infinite binary sequence
  • 이것의 집합을 본다. $\mathbb{B}$
  • 이것은 uncountable이다.
• $\mathbb{B}$가 countable이면 $\mathbb{N} \overset{f}→ \mathbb{B}$이다.
• $\mathbb{B}$에 포함된 x가 있다.
  • 이 x는 n과 대응되는 f(n)의 반대이다.
  • 예를 들어, f(1) = 00000..., f(2) = 11111..., f(3) = 010101...이면 $x = 101...$이렇게 가는 것이다.
  • 그러면 x는 대응되는 것이 없으므로 N과 B의 개수는 다르며, $B$의 개수가 더욱 많다.
• 이제 $\mathbb{L}$을 보자. $\mathbb{L}=\mathbb{B}$이다.
• $\mathbb{L}$중 하나를 뽑아보자. $l_1$은 0의 개수가 짝수인 language이다.
• $Σ^* = {,0,1,00,01,10,11,000,..., }$로 순서를 정렬한다.
• 이 중 $l_1$은 $l_1 = {,0,1,00,11,001,..,}$이렇게 된다.
• 순서에 맞게 들어가는 걸 $\mathbb{X_{l_1}}$이라고 해보자. 그러면 $\mathbb{X_{l_1}} = {011001..}$이렇게 진행된다.
• $\mathbb{X_{l_1}}$는 하나의 실수값을 가지게 된다.
• 모든 language에 대해서 이것을 수행하면, 모든 language는 실수개라는 것을 알게 된다.
  
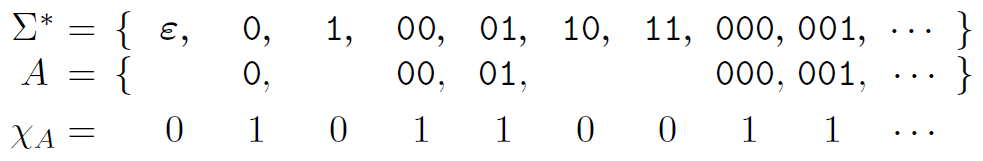
• 따라서 $\mathbb{B}$가 uncountable이므로, $\mathbb{L}$도 uncountable이다.

Halting problem is undecidable

$A_{TM}$은 undecidable하다.

거짓말쟁이 역설

A = 이 명제는 거짓이다.

• A는 사실이다.
  • 그렇게 되면 "A = 이 명제는 거짓이다"가 사실이므로 A가 A'가 된다. 하지만 A'가 아닌 A가 되어야 하므로 역설이 발생한다.
• A는 거짓이다.
  • 그렇게 되면 "A = 이 명제는 거짓이다"가 거짓이므로 A는 A가 된다. 하지만 명제에 따르면 A가 아닌 A'가 되어야 하므로 역설이 발생한다.

halting problem

• $HALT_{TM}$은, 어떤 TM이 input을 받았을 때 halt할지 하지 않을지를 알려준다.(accepting or rejecting)
• 이런 $HALT_{TM}$이 있는지 없는지에 대한 것을 halting problem이라고 한다.
• $HALT_{TM} = \{⟨M, w⟩ | M$은 TM이며, M은 input $w$를 받으면 halt한다.$\}$
• 이걸 프로그램으로 바꿔본다.
  • input : ⟨program p⟩, ⟨input i⟩
  • output
    • (1) : true, p가 i를 받아서 종료함
    • (2) : false, p가 i를 받아서 종료하지 않고 loop forever함
• 이런 프로그램을 trouble이라고 생각해보자.

1: function trouble(string s){
2:   if (halt(s, s) == false)
3:     return true;
4:   else
5:     loop forever; // while(1){};
6: }

• 프로그램 trouble은 string으로 표현될 수 있다.
• 모든 프로그램을 string으로 표현할 수 있으므로, 위의 프로그램 trouble은 string $t$로 변환할 수 있다.
• 이 string $t$를 입력으로 하는 trouble(t)에 대해서 생각해보자.
  • (1) : trouble(t)가 halt하려면, halt(t,t) == false여야 한다. 그러려면 trouble(t)가 false여야 한다. 이 말은 trouble(t)가 halt하지 않아야 한다. 이는 처음에 말한 trouble(t)는 halt해야 한다는 것과 모순이다.
  • (2) : trouble(t)가 loop forever하려면, halt(t,t) == true여야 한다. 그려려면 trouble(t)가 true여야 한다. 이 말은 trouble(t)가 halt해야 한다. 이는 처음에 말한 trouble(t)가 loop forever해야 한다는 것과 모순이다.
• 그러므로 어떠한 상황이든 trouble(t)에 대해서 모순이 생긴다. 그러므로 trouble은 존재할 수 없다.
• 이 말은 입력으로 받은 프로그램이 종료하는지를 판별하는 프로그램 halt는 존재할 수 없다는 의미이다.

Turing-unrecognizable Language

• $A_{TM}$은 undecidable하다.
• 이제, $\overset{-}{A_{TM}}$을 생각해보자. 어떤 문제는 Turing-decidable이 아니다.
• 지금까지를 정리하면, 어떤 language와 그 language의 complement가 Turing-Recognizable이면, language는 decidable하다.
• $A:TR \& \bar{A}:TR -> A:TD$
• $A$가 TD가 아니므로 A는 TR이 아니거나 A의 complement가 TR이 아니다.
• co-Turing-recognizable = A의 complement

어떤 language가 decidable하면, language는 Turing-recognizable하며 co-Turing-recogniable하다.

• $A:TD → A:TR \& \bar{A}:TR$
  • $A:TD → A:TR$은 당연하다.
  • 문제는 $A:TD → \bar{A}:TR$이다.
  • $A$는 Accept하는것들이 있으며, 나머지는 Reject한다.
  • $\bar{A}$는 Accept하거나, Reject해야한다.
  • $\bar{A}$는 $A$가 Accept하는 것을 Reject한다.
  • $\bar{A}$는 $A$가 Reject하거나 loop하는 것을 Accept해야 한다.
  • 그러므로 $\bar{A}$는 Turing-recognizable하다.
• $A:TR \& \bar{A}:TR → A:TD$
  • $A : TR$이므로, $A$는 accept하는 것들이 있으며, 나머지는 reject하거나 loop한다.
  • $\bar{A} : TR$이므로, $A$가 reject하거나 loop하는 것을 Accept할 수 있고, A가 accept하는 것은 reject한다.
  • 그러므로 어떤 string을 $A:TR$인 $M_1$과 $\bar{A}:TR$인 $M_2$ 둘 다에 병렬적으로 넣어본다.
  • 만약 $M_1$이 accept하면, A는 accept한다.
  • 만약 $M_2$가 accept하면, A는 reject한다.
  • 그러므로 A는 accept하거나, reject한다. 이 두가지밖에 없으므로 TD라고 할 수 있따.

$\bar{A_{TM}}$은 Turing-Recognable이 아니다.
$\bar{A_{TM}} : TR$이 아니다.

• $A_{TM} : TR$이다.
• 그러나 $A_{TM} : TD$가 아니다
• 그러므로 $A:TR \& \bar{A}:TR → A:TD$에서 $A:TR$, $\bar{A}:TR$ 둘 중 하나는 거짓이여야 한다.
• 위에서 $A_{TM}:TR$이라고 했으므로 결론적으로 $\bar{A_{TM}}:TR$이 아니다.
  • 중요한 것은 $\bar{A_{TM}}:TR$이 아니라고 해서 답을 못낸다는 의미는 아니다. $A_{TM}:TR$의 반대이므로 $A_{TM}$이 accept하는 것은 $\bar{A_{TM}}$이 reject한다. 또한 $A_{TM}$이 reject하는 것 중 $\bar{A_{TM}}$이 accept하는 것들도 존재한다. 하지만 accpet를 하지 못하는 loop가 존재한다는 의미이다.

정리

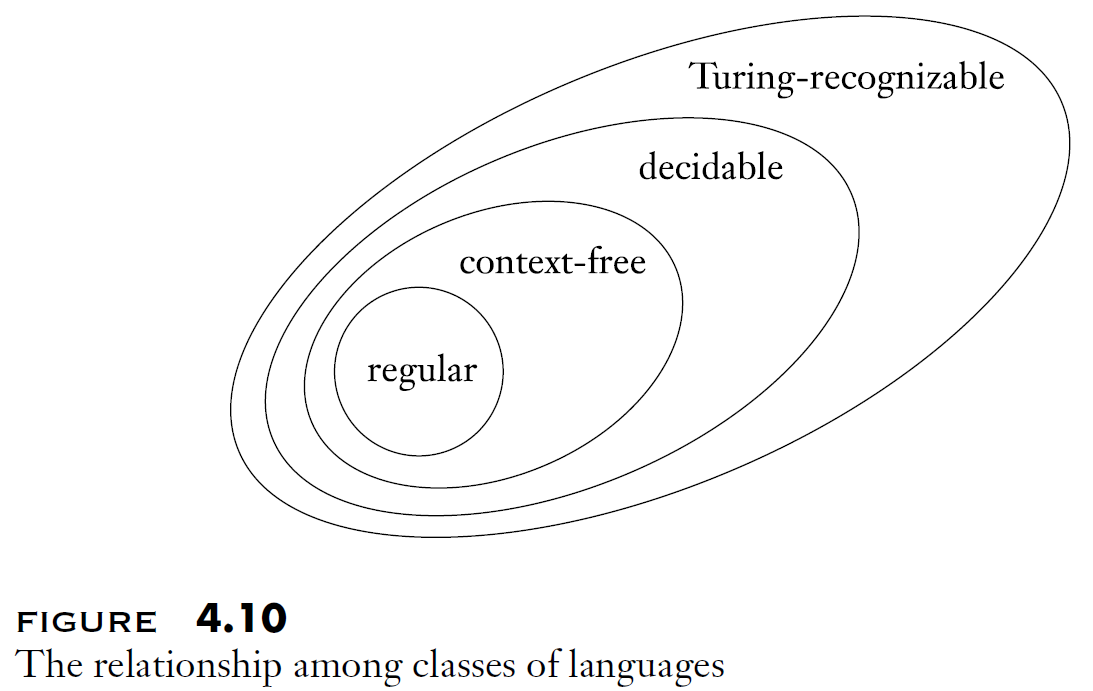
• 어떤 문제를 마주했다.
• 문제 : language이다.
• Finite Automata정도로 답을 낼 수 있는 문제는 regular language라고 한다.
  • DFA
  • NFA
  • 전자 회로 수준
• Finite Autotmata로 풀 수 없는 문제들이 존재한다.
• 이 문제들 중 Context-Free Grammer를 따라서 Pushdown Automata로 풀 수 있는 문제를 Context-Free Langauge라고 한다.
  • 꽤 많은 문제들은 이 정도 수준에서 풀린다.
  • PDA,NPDA
• Pushdown Automata로 풀 수 없는 문제들이 존재한다.
• 이 문제들 중 Turing Machine으로 풀 수 있는 문제들이 있다.
  • 하나의 Turing Machine은 모든 튜링 머신을 따라할 수 있다. 이 Turing Machine을 Universal Turing Machine이라고 부르며, 여러가지 일을 수행할 수 있기 때문에 현대 컴퓨터의 기초가 된다.
• Turing Machine으로 accept / reject의 값만 낼 수 있는 문제를 decidable이라고 부른다.
• Turing Machine에 문제를 넣었을 때, 무한히 loop하는 문제들을 포함한 것을 Turing-recognizable이라고 부른다.
• Turing-recogniable로 말할 수 없는 문제들을 Turing-unrecognizable이라고 부른다.