회로의 빼기 연산과 가감산기

이진수의 빼기 연산

빼기는 사실 음수의 덧셈으로 치환할 수 있다. $A - B$에 대해서 $A + (-B)$로 말해도 된다는 의미이다. 그렇기 때문에 음수에 대해서 먼저 아는 것이 중요하다.

음수 표현에 대해서는 보수를 참조하자.

뺄셈기

전가산기(full adder)를 잘 활용하면 뺄셈기도 만들 수 있다. 위에서 설명한 것처럼 빼기는 음수의 덧셈으로 치환 가능하기 때문에 보수와 덧셈기의 원리를 잘 이해한다면 뺄셈기를 만들 수 있다.

$A - B => A + B' + 1$로 바꿀 수 있으며, 여기서 $B' + 1$은 $B$를 2의 보수로 바꾼 것이다. 그러므로 $B$의 입력에 NOT연산을 하고, 처음 들어오는 $C_{in}$을 1로 바꾸면 된다.

---

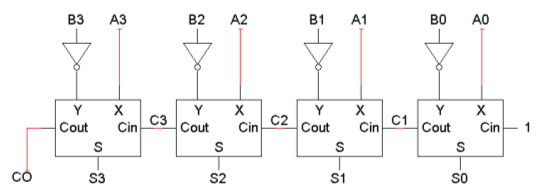
덧셈기와 뺄셈기의 조합 회로

덧셈기와 뺄셈기는 구조가 비슷하다. 그러면 두 회로를 하나로 합할 수 있을까?

덧셈기와 뺄셈기의 차이

덧셈기와 뺄셈기는 두가지 차이가 있다.

• $B$의 입력이 서로 반대된다.
• $C_{in}$의 입력값이 반대된다.
  이 두개를 구분할 수 있으면 덧셈과 뺄셈 또한 구분할 수 있다.

가감산기(add-subtractor)

XOR(Exclusive-OR)를 활용하면 덧셈과 뺄셈에 대한 다른 연산을 수행할 수 있다.
다음과 같은 X가 있을 때 XOR를 이용하면 이런 식을 만들 수 있다.
$X\bigoplus0 = X$, $X\bigoplus1 = X'$
이를 이용하여 B의 입력값을 바꿀 수 있다.

• 먼저 B의 앞에 XOR를 추가한다.
• 새로운 Sub를 만들어 B의 앞 XOR에 넣는다.
• 이를 통해 B의 자리수에 해당하는 값과 Sub신호를 받는 XOR가 자리수마다 만들어진다.
• $C_{in}$도 sub신호를 받는다.
  
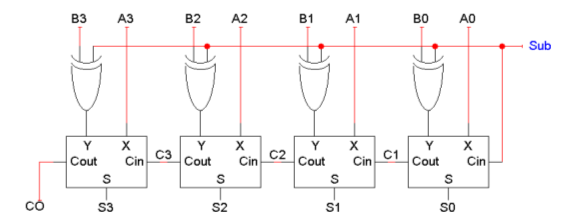
  위 회로는 설명한 내용을 구현한 회로다. 가감산기(add-subtractor)라고 부른다. 덧셈일때 sub는 0이고, 뺄셈일때 sub는 1로 설정한다. 이를 통해 덧셈과 뺄셈을 바꿀 수 있으며 한 회로에서 두가지 일을 수행할 수 있다.

---

signed overflow

sign bit를 사용하면 overflow가 발생할 수 있으며, 이는 연산 결과값을 바꾸거나 부호를 변화시키는 문제를 초래할 수 있다.
$0100_{2}(+4)$와$0101_{2}(+5)$의 더하기를 해보면 $01001_{2}(+9)$가 나온다. 여기서 결과값이 4bit라고 하면 $1001_{2}(-7)$가 나온다.
이런 문제는 부호가 같은 숫자를 더했을 때 최대 비트를 넘어가면서 결과값이 다르게 나오는 overflow현상이다.

overflow 검출

sign bit에서 overflow는 다음과 같은 상황일 때 발생한다

• 마지막 carry에 들어오는 숫자가 0이고 그 전 carry의 숫자가 1일때
• 마지막 carry에 들어오는 숫자가 1이고 그 전 carry의 숫자가 0일때
  결과적으로 마지막 carry에 들어오는 숫자와 그 전 carry의 숫자가 다를 때 overflow가 발생한다는 것을 알 수 있다.
  
  서로가 다르다는 것을 확인하는 방법은, 우리가 많이 했던 XOR를 활용하면 된다...
  
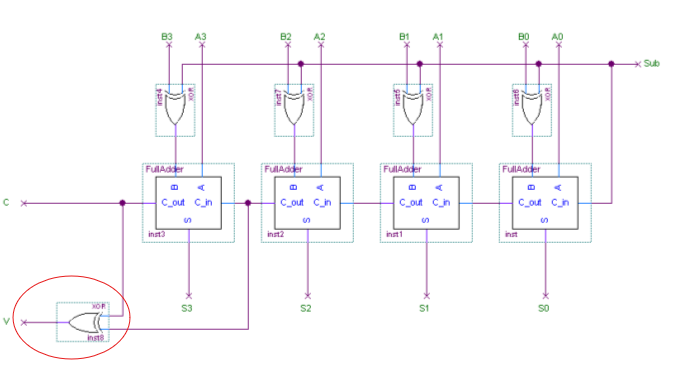
  overflow 검출을 확인하는 기능이 달린 가감산기다. 마지막 carry와 그 전 carry를 받아서 XOR를 통해 만약 1이 나오면 overflow가 발생했음을 알린다.