회로의 더하기 연산

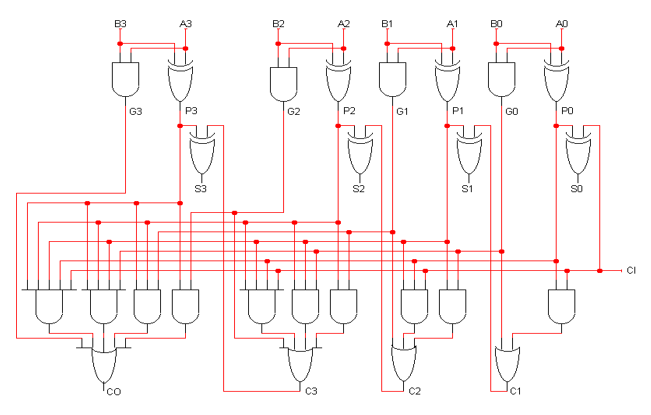
이진수의 더하기 연산

이진수의 더하기 연산은 Carry를 통해서 이루어진다. Carry와 두 피연산자의 자리수를 통해서 답을 낼 수 있다.

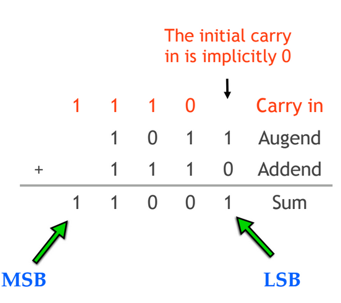
두 비트 더하기 연산

두 비트를 더하는 연산은 다음과 같이 정의할 수 있다.
$f(X,Y) = (C,S)$, $C = XY$, $S = X'Y + XY' = X \bigoplus Y$
이를 반가산기(half adder)라고 부른다.

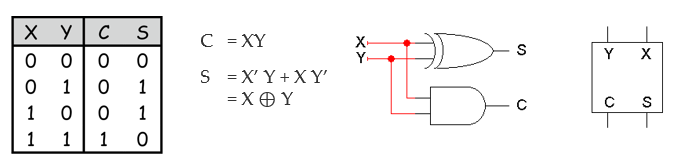
세 비트 더하기 연산과 전가산기

덧셈을 할 때는 Carry를 고려하므로 실제 연산은 세 비트를 더하는 연산을 수행해야한다.
$f(X,Y,C_{in}) = (C_{out},S)$,
$C_{out} = (X \bigoplus Y)C_{in} + XY$,
$S = X \bigoplus Y \bigoplus C_{in}$
이를 전가산기(full adder)나 덧셈기라고 부른다.

---

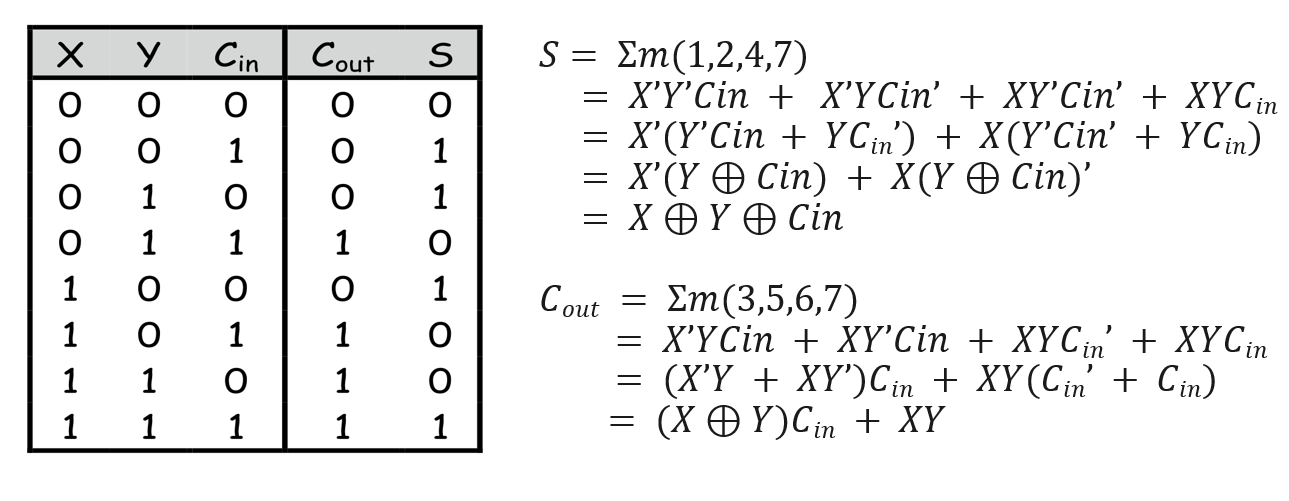
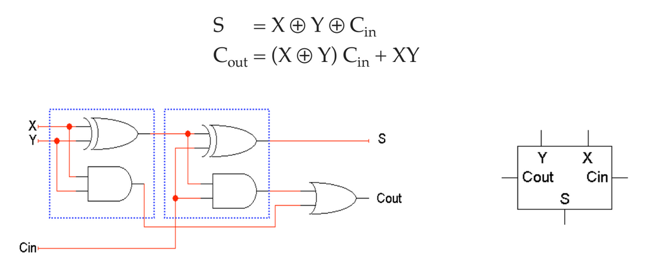
이진수 더하기 연산 설계

네 비트 숫자 2개의 더하기 연산

네 비트로 이루어진 숫자 2개를 연산한다고 하자.
숫자 A,B가 있을 때, 각자 $A0A1A2A3$, $B0B1B2B3$이며, 처음 Carry CI가 있다. 이것에 대한 결과 $S0S1S2S3$가 있고, Carry out CO가 있다.
결국 네 비트 연산 장치는

• 9개의 입력 $A0A1A2A3$, $B0B1B2B3$, CI
• 5개의 출력 $S0S1S2S3$, CO로 구성된다.
  전가산기의 직렬 연산으로 이루어지며, CI와 CO의 추가 입력을 통해 회로를 구현할 수 있다.
  
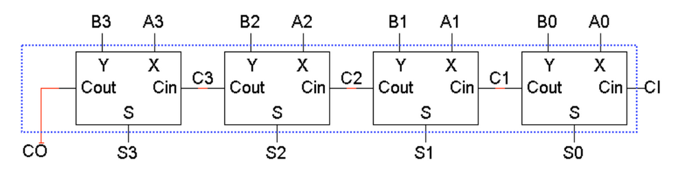
  ex) A=1011(11), B=1110(14), S=11001(25)
  

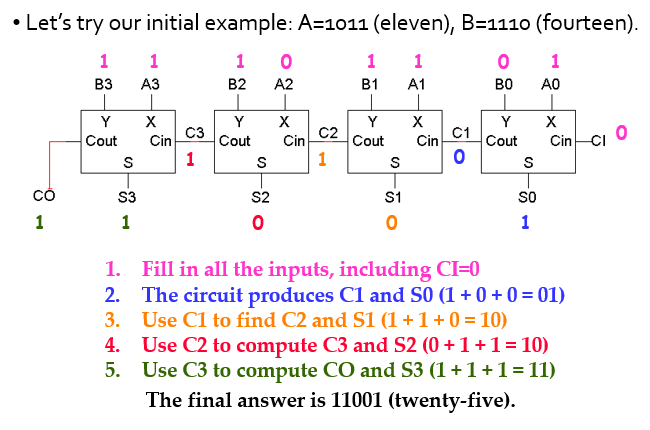
위의 정답인 11001은 4비트에서 5비트의 결과로 1비트가 늘어났으므로, 만약 연산체계가 4비트면 결과도 4비트만 저장할 수 있다. 자리수를 넘어가는 상황을 overflow라고 한다.

계층적 설계(더하기)

이미 만들어있는 회로를 연결하여 더 나은 회로를 설계하는 방법을 계층적 설계라고 한다. 위의 4비트 더하기 연산 회로의 CO와 CI를 연결하면 8비트 더하기 연산 회로를 만들 수 있다.

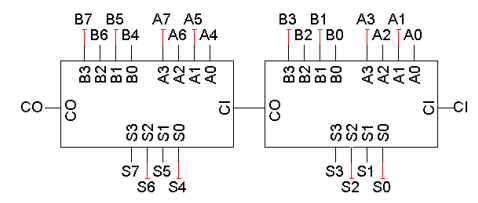
이때 중요한 건 매핑(mapping)이다. 만약 같은 회로를 사용하면 내부에 있는 요소들은 index를 유지하되, 회로 전체에서는 논리에 맞게 연결해줘야 한다. 같은 회로를 사용하지만 내부 요소가 달라지면 같은 회로가 아니게 되어버리며, 앞 회로와 뒤 회로의 연결이 섞이면 원하는 결과가 나오지 않게 된다.

---

게이트 지연과 해결방법

게이트 지연

게이트는 물리적인 회로이기 때문에 신호가 바뀌는 과정에서 필수적으로 시간 지연이 일어날 수 밖에 없다. 이를 gate delay(게이트 지연)라고 한다.

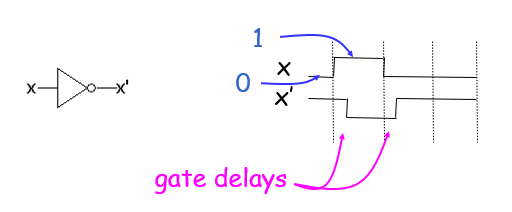
Ripple carry

다음은 전가산기가 연결되어 있는 구조다. 이를 ripple carry라고 부른다. ripple carry는 nbit 연산 당 2n+1개의 게이트를 지나야 하며, 이는 2n+1개의 게이트를 지나야 한다는 의미이다. 그만큼 게이트 지연이 일어나게 되므로 n이 증가할 수록 굉장히 느려진다.

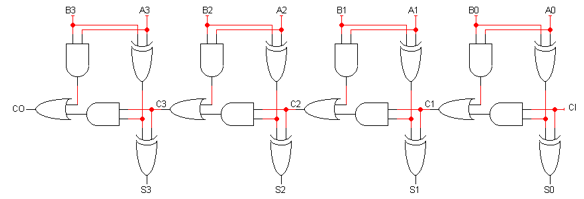
더 빠른 방법

함수를 다음과 같이 정의한다.
$g_{i} = A_{i}B_{i}$
$p_{i} = A_{i} \bigoplus B{i}$
$c_{i+1} = g_{i} + p_{i}c_{i}$

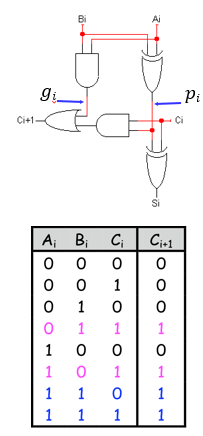
우리는 $c_{i}$에 대한 일반식을 만들었다.

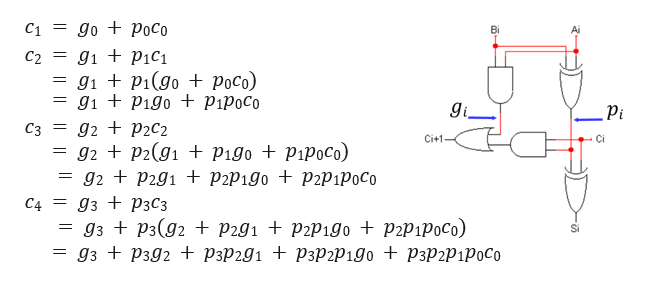
이를 통해 모든 $c_{i}$를 $g_{i}$와 $p_{i}$로 표현할 수 있다. 4개의 gate delay만 거치면 정답을 도출할 수 있다.