[GN] 11. Graph Neural Networks (Cont'd)

Week 11. Graph Neural Networks (Cont'd)

Generalization of GCN -> GNN

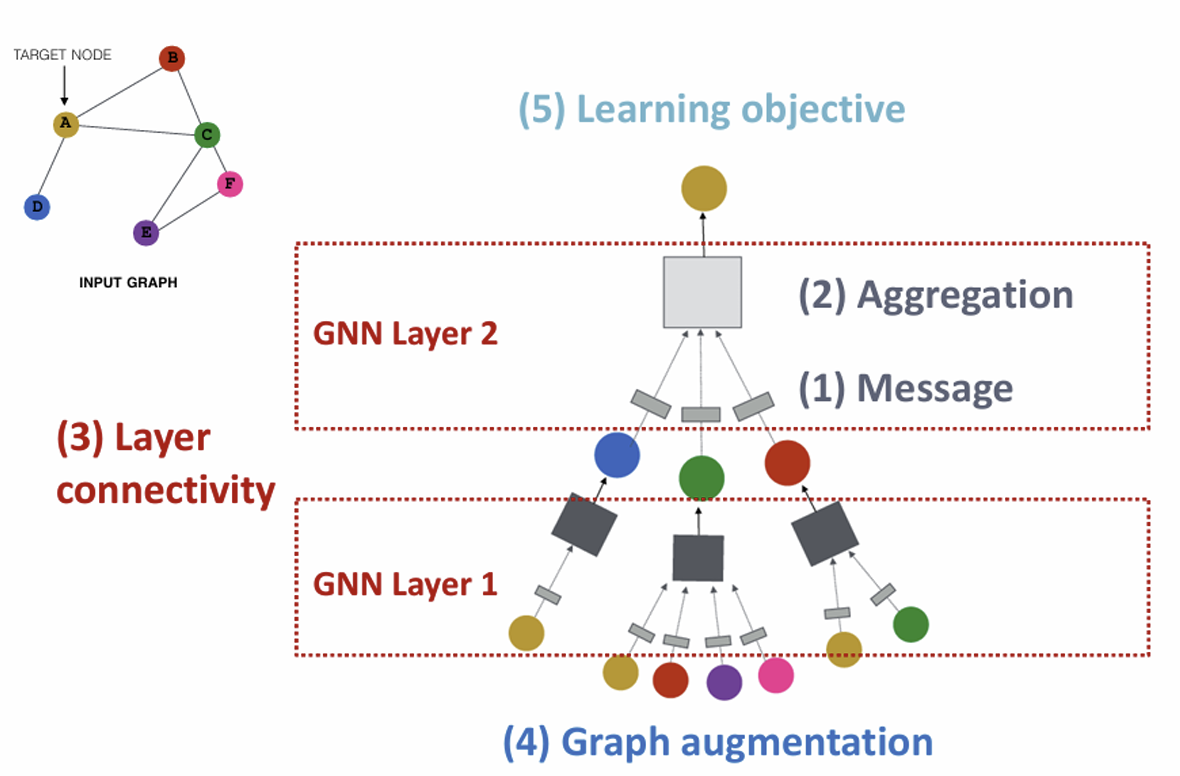
1. A Single Layer of GNN

A GNN Layer
GNN Layer = Message + Aggregation
Idea of a GNN Layer
• Compress a set of vectors into a single vector
• Two-step process:
1. Computing message
2. Aggregation

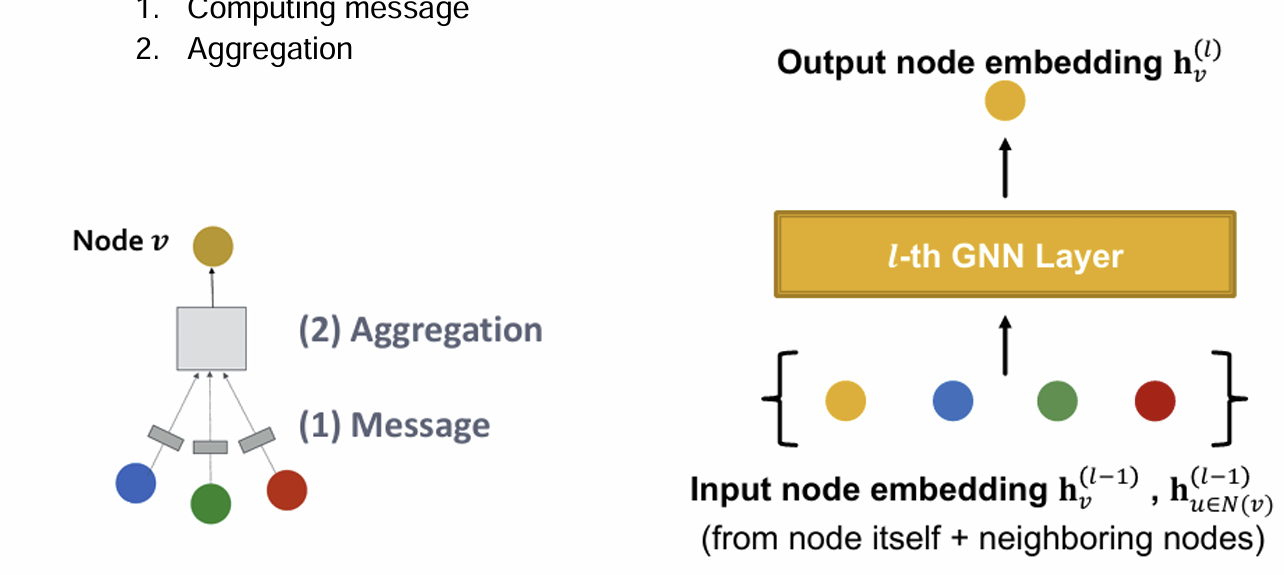
(1) Message Computation
Message function $m_u^{(t)} = MSG^{(t)}(h_u^{(t - 1)})$
• Intuition: Each node will create a message, which will be sent to other nodes later
• Example: A linear layer $m_u^{(t)} = W^{(t)}h_u^{(t - 1)}$
Multiply node featrues with weight matrix

(2) Message Aggregation
Aggregation function: $h_v^{(t)} = AGG^{(t)}({m_u^{(t)}, u \in N(v)})$
• Intuition: Each node will aggregate the messages from node 𝑣’s
neighbors
• Example: Sum(⋅), Mean(⋅) or Max(⋅) aggregator
$h_v^{(t)}$ = Sum^{(t)}({m_u^{(t)}, u \in N(v)})$

• Do not Forget Self-features
  Issue: Information from node 𝑣 itself could get lost
  Computation of $h_v^{(t)}$ does not directly depend on $h_v^{(t-1)}$
  Solution: Include $h_v^{(t-1)}$ when computing $h_v^{(t)}$
  Message: compute message from node v itself
  Aggregation: After aggregating from neighbors, we can aggregate the message from node 𝑣 itself
  자기 feature를 잊지 말고 명시적으로 넣어주라, 어디 들어 있는지 확인 필요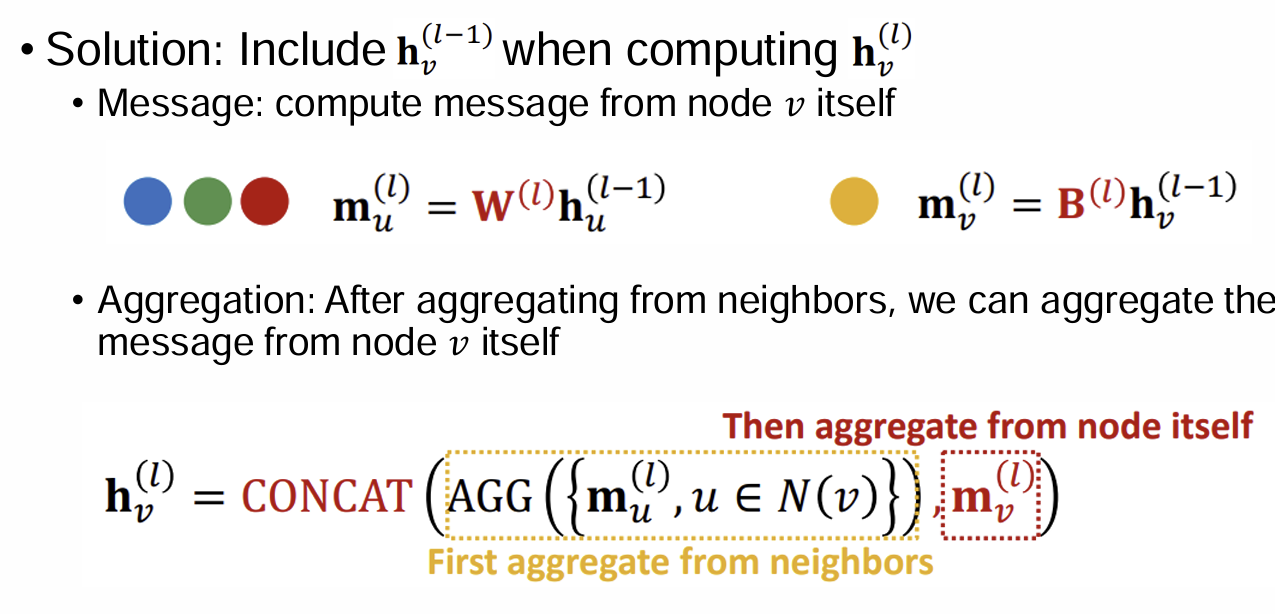

  

• Putting things together
  앞에 수식 가져오기
  Nonlinearity (activation): Add expressiveness
  sigma, ReLU, Sigmoid- message, aggregation에 모두 적용 가능

Classical GNN Layers: 1. GCN
GCN Formula -> Message + Aggregation
Message: Normalized by node degree
Aggregation: sum messages, then activation
few notes: another representation: MSG = Node features, AGG = avg, self-feature temrm may be in the summation (u \in N(v))
message computation, aggregation이 조금 다름

Classical GNN Layers: 2. GraphSAGE
Formula -> Message + Aggregation
AGG
Two-stage aggregation
Stage 1: Aggregate from node neighbors- functions in next page
Stage 2: Further aggregate over the node itself

Aggregation Functions in GraphSAGE
Mean: take a weighted average of neighbors
Pool: Transform neighbor vectors and apply symmetric vector function Mean(⋅) or Max(⋅)
LSTM: Apply LSTM to reshufffled of neighbors
aggregation을 다양하게 할 수 있음

L2 Normalization in GraphSAGE
applies at every layer
Without L2 normalization, the embedding vectors may have different scales for vectors. After L2 normalization, all vectors will have the same scales
performance improvement, quick convergence while training
평균을 0으로

Classical GNN Layers: 3. Graph Attention Network (GAT)
Motivation: GCN, GraphSAGE, all neighbors u are equally important to node v- weighting factor is same
Now we differetiate the weights- next page

CF) Attention Mechanism
The attention score focuses on the important parts of the input data and fades out the rests
• Idea: the NN should devote more computing power on that small but important part of the data.
• Which part of the data is more important depends on the context and is learned through training.
Query - Key 중요도 계산- Value에 곱함

Classical GNN Layers: 3. Graph Attention Network (GAT) cont'd

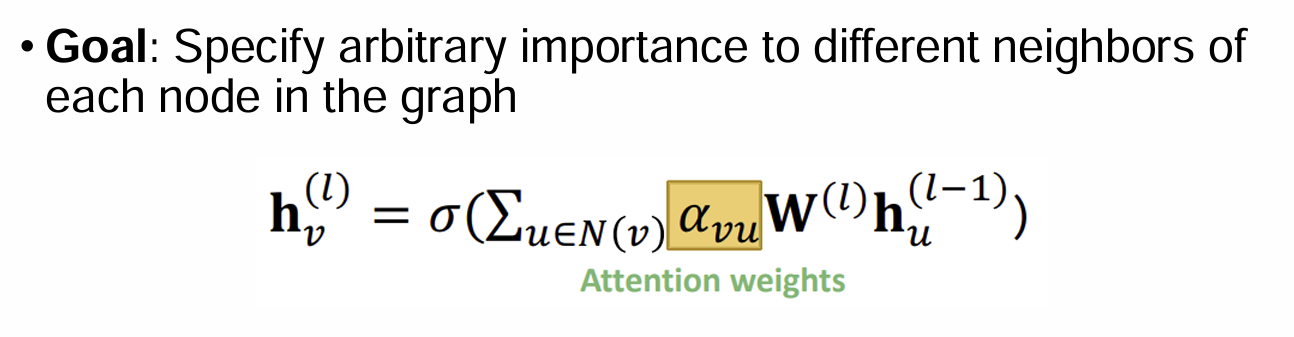
Idea: Compute embedding h_v following an attention strategy:
Node attend over their neighborhoods' message
Implicitly specifying different weights to different nodes in a neighborhood

Computing Attention in GAT
Assumption

• Step 1: compute attention coefficient $e_{vu}$
  a: dot product
  $e_{AB}$: single value

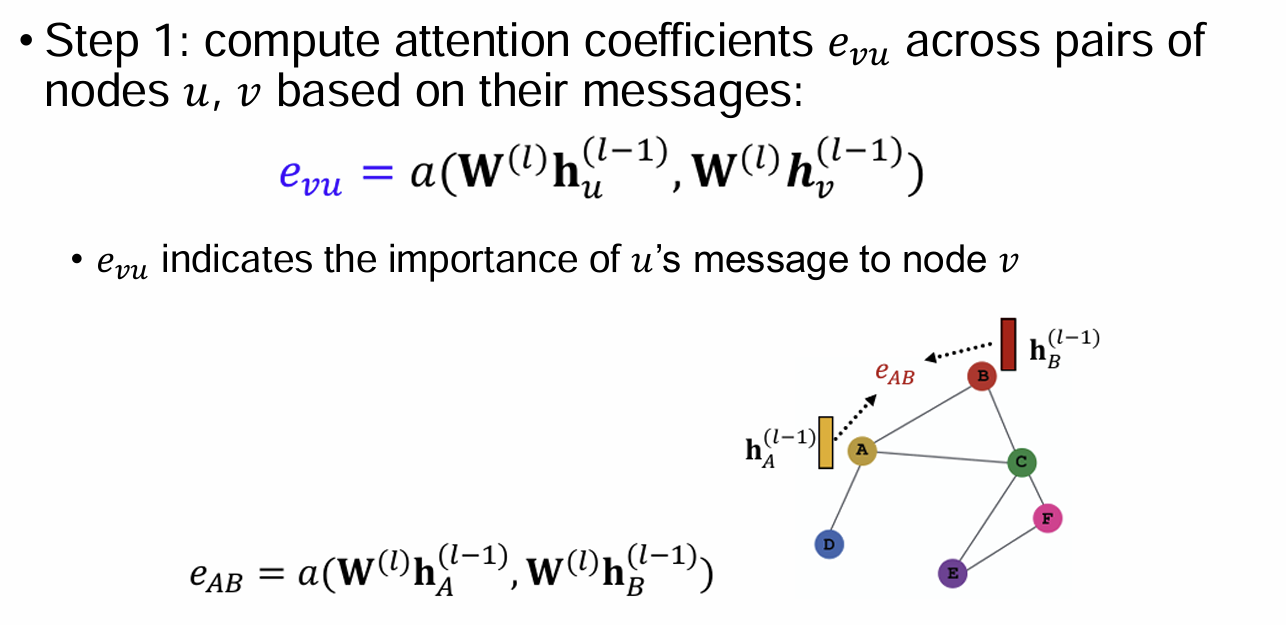
• Step 2: normalize $e_{vu}$ $\alpha_{vu}$
• Step 3: compute weighted sum

Some Notes on GAT
agnostic 불가지론- 모른다
Multi-head attention 사용 가능

Benefits of Attention Mechanism
Key Benefit: Allows for (implicitly) specifying different importance values ($\alpha_{vu}$) to different neighbors
• Computationally not expensive:
Computation of attentional coefficients can be parallelized across all edges of the graph
Aggregation may be parallelized across all nodes
• Storage not expensive
Sparse matrix operations do not require more than 𝑂(𝑉 +𝐸) entries to be stored
Fixed number of parameters, irrespective of graph size
• Localized:
Only attends over local network neighborhoods (i.e., not expensive)
• Inductive capability:
It is a shared edge-wise mechanism
It does not depend on the global graph structure

2. A Single Layer of GNN in Practice

GNN Layer in practice
many modern deep learning modules 사용 가능

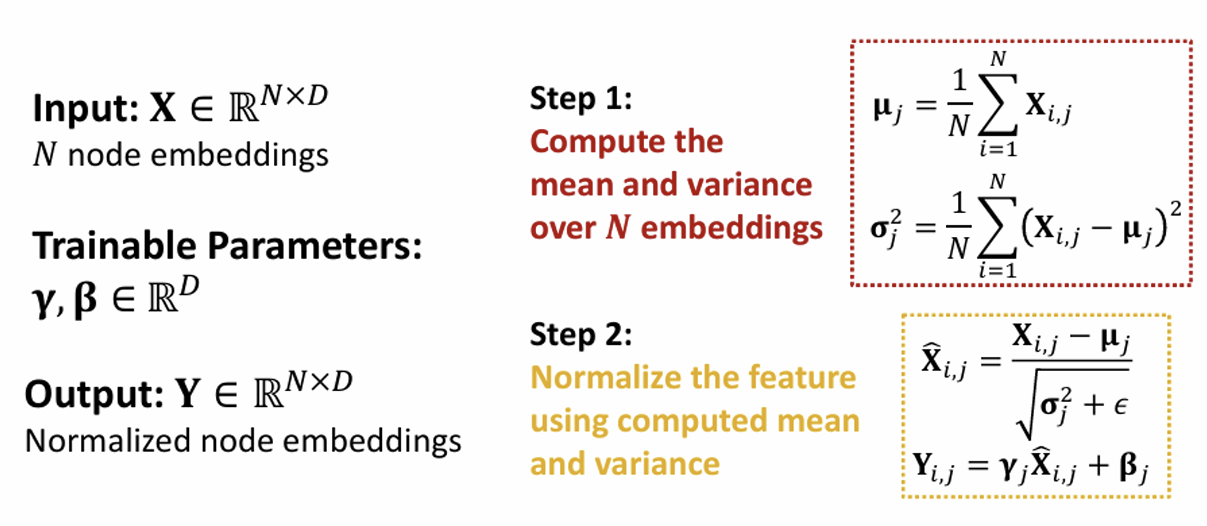
Batch Normalization
• Goal: Stabilize neural networks training
• Idea: Given a batch of inputs (node embeddings)
Re-center the node embeddings into zero mean
Re-scale the variance into unit variance
Step: compute the mean, variance
Normalize the feature

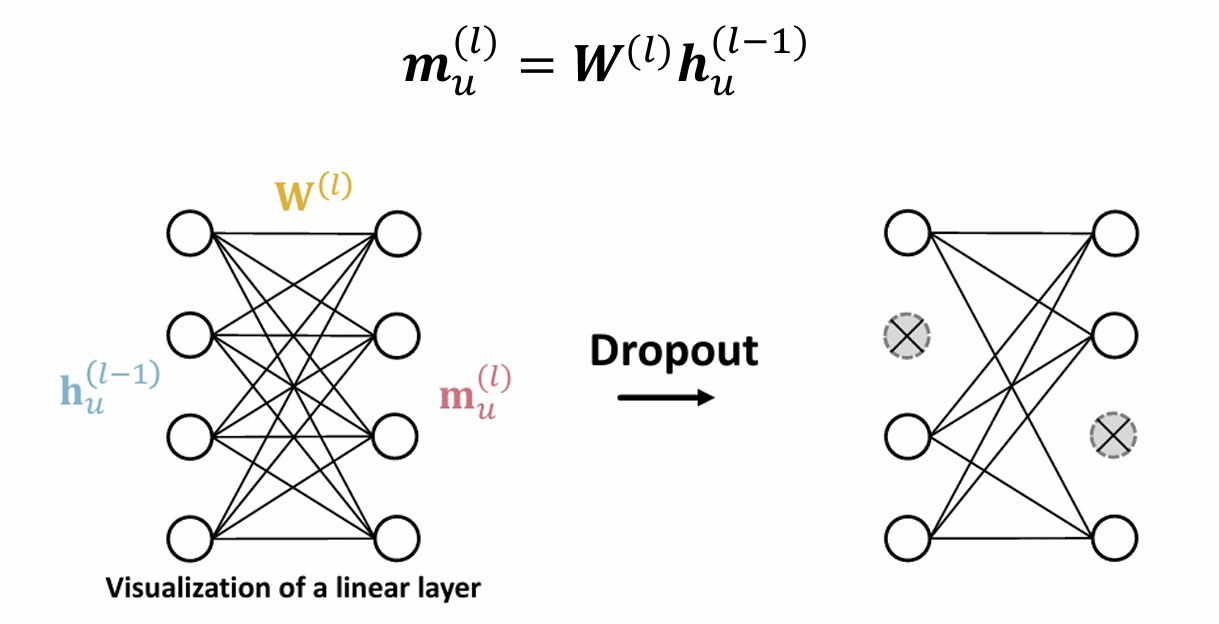
Dropout
• Goal: Regularize a neural net to prevent overfitting.
• Idea:
During training: with some probability 𝑝, randomly set neurons to zero (turn off)
During testing: Use all the neurons for computation

Activation (Non-linearity)
ReLU
Sigmoid (0,1)
Parametric ReLU

3. Layer Connectivity