[GN] 5. PageRank

Week 5-2. PageRank

1. PageRank

assigns a PageRank(- score, measure of importance) to each webpage
graph = web
nodes = web pages
edges = hyperlinks
navigational(page to page) -> transactional(post, comment, like)

• idea: LINKs as Votes
  in-coming links, from important pages(recursive) important

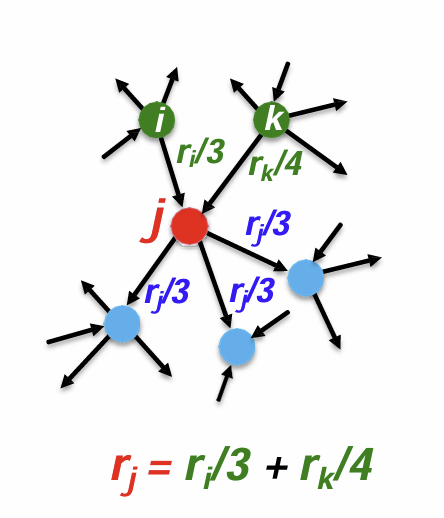
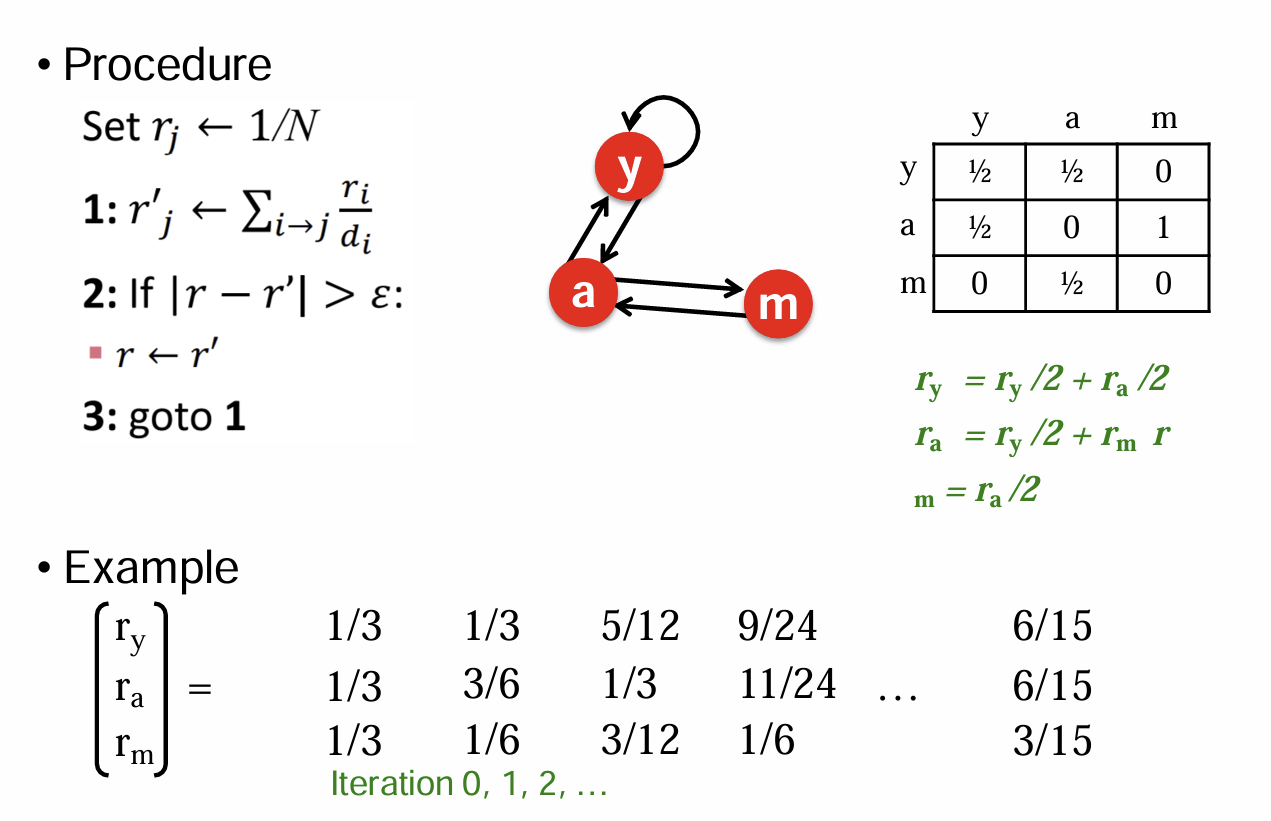
Beginning of PageRank: The "FLOW" Model
each link's vote, source page의 importance와 비례
page i with importance $r_i, d_i$ out-links- $\frac{r_i}{d_i}$ votes
page j rank $r_j$: sum of the votes on in-links
$\displaystyle r_j = \sum_{i \rightarrow j}\frac{r_i}{d_i}$

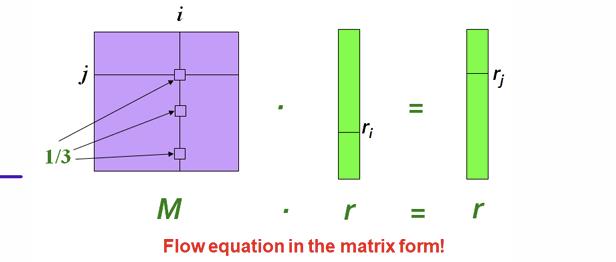
PageRank: Matrix Formulation

• Stochastic adjacency matrix M
  page j has $d_j$ out-links
  if j -> i, then $M_{ij}=\frac{1}{d_j}$
  columns sum to 1
• Rank vector r: an entry per page
  $r_i$: importance score of page i
  $\sum_ir_i = 1$
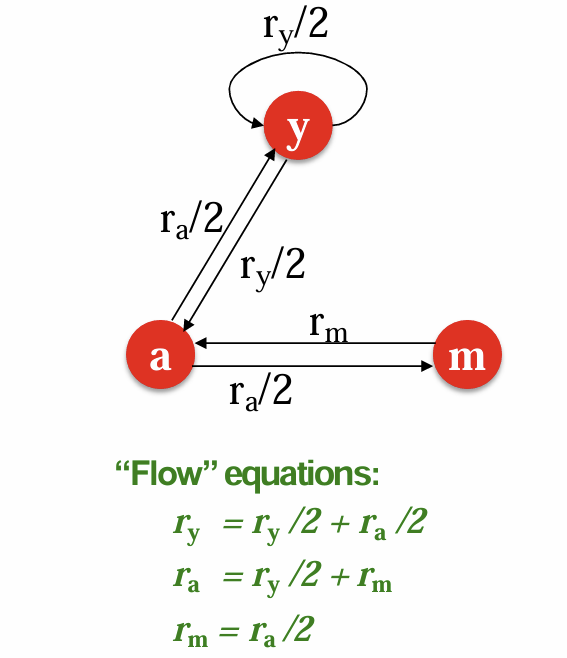
• The flow equations
  $r = M\centerdot r$

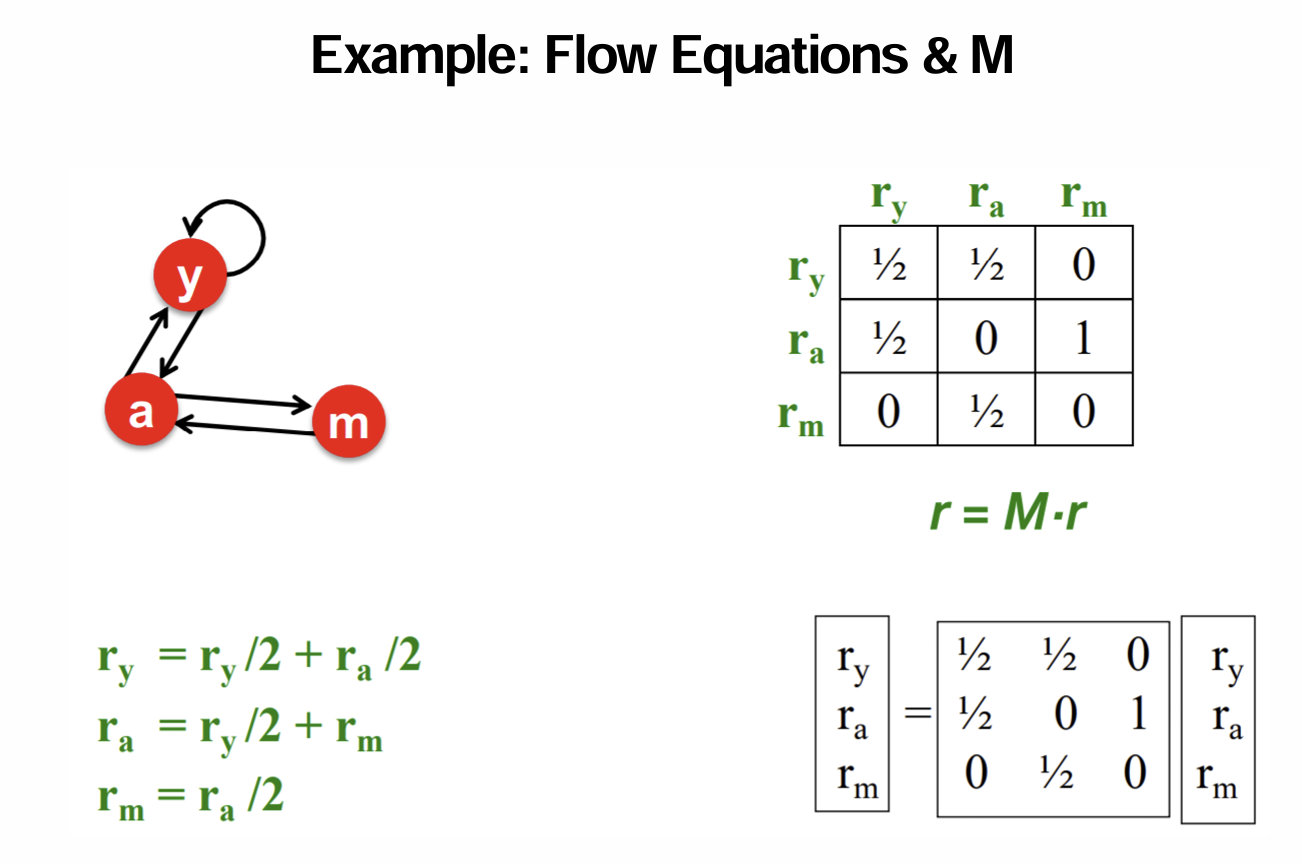
2. Solving PageRank

Gaussian elimination -> bad, too much cost
Power Iteration
n nodes, initialize, iterate, repeat until convergence
L1 norm

Two Problems: Dead Ends & Spider Traps
Dead ends: no out-links
Spider traps: all out-links are within the group

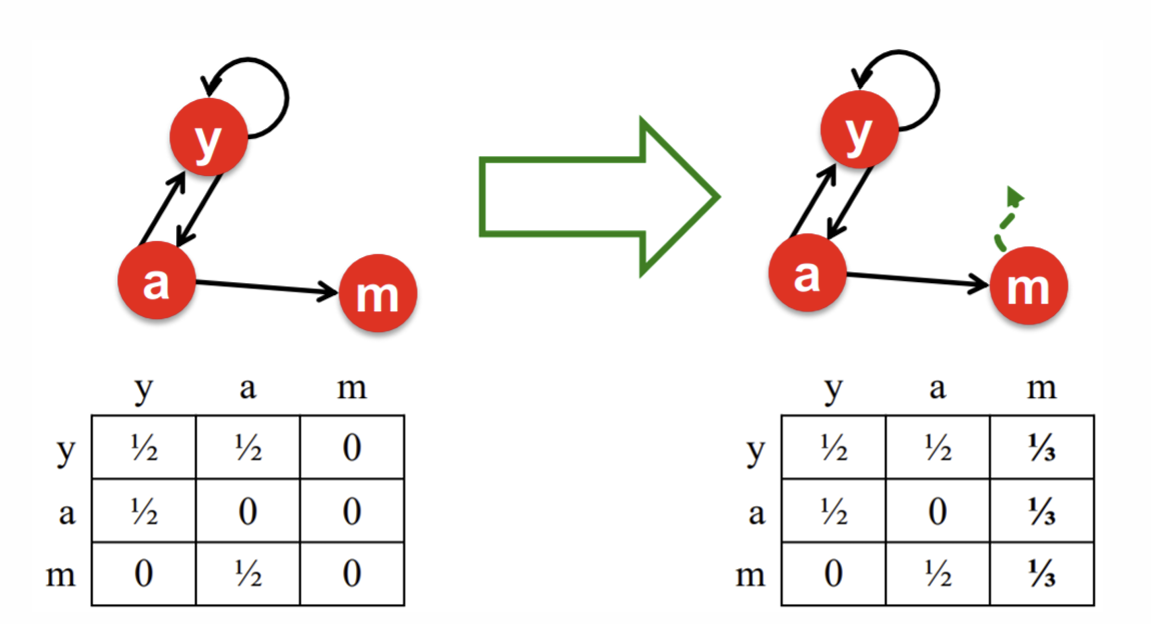
Solution: Teleports

• For Spider traps: random surfer
  prob $\beta$ follow a link at random
  prob $1 - \beta$ jump to a random page
• For dead-end: follow random teleport links with total probability 1.0 from dead-ends
  adjust matrix accordingly
  000이면 무조건 random teleport

Final Solution: Random Teleports

• PageRank equation
  $\displaystyle r_j = \sum_{i \rightarrow j}\beta\frac{r_i}{d_i} + (1 - \beta)\frac{1}{N}$

• Google Matrix G
  $\displaystyle G = \beta M + (1-\beta)\left[\frac{1}{N}\right]_{N\times N}$
  recursive problem: $r = G \centerdot r$
  power method still works
  $\beta$ = 0.8,9 (5 steps on average to jump)

3. Topic Specific PageRank

Modified Scenarios with Topic-Specific PageRank
1. Model the web as a graph
2. Compute the importance of webpages with PageRank
3. Web-search query
The user types the query “Trojan”
4. Identify relevant webpages
Find webpages relevant to “Trojan”
-> compute the importance of webpages based on their relevance to a topic
5. Show them to the user
Webpages with high generic -> topic-specific PageRank will be presented first

Goal: Evaluate Web pages by how close they are to a particular
topic, e.g. “sports” or “history”
search queries answered based on the interests of a user, e.g. “sports” or “history”

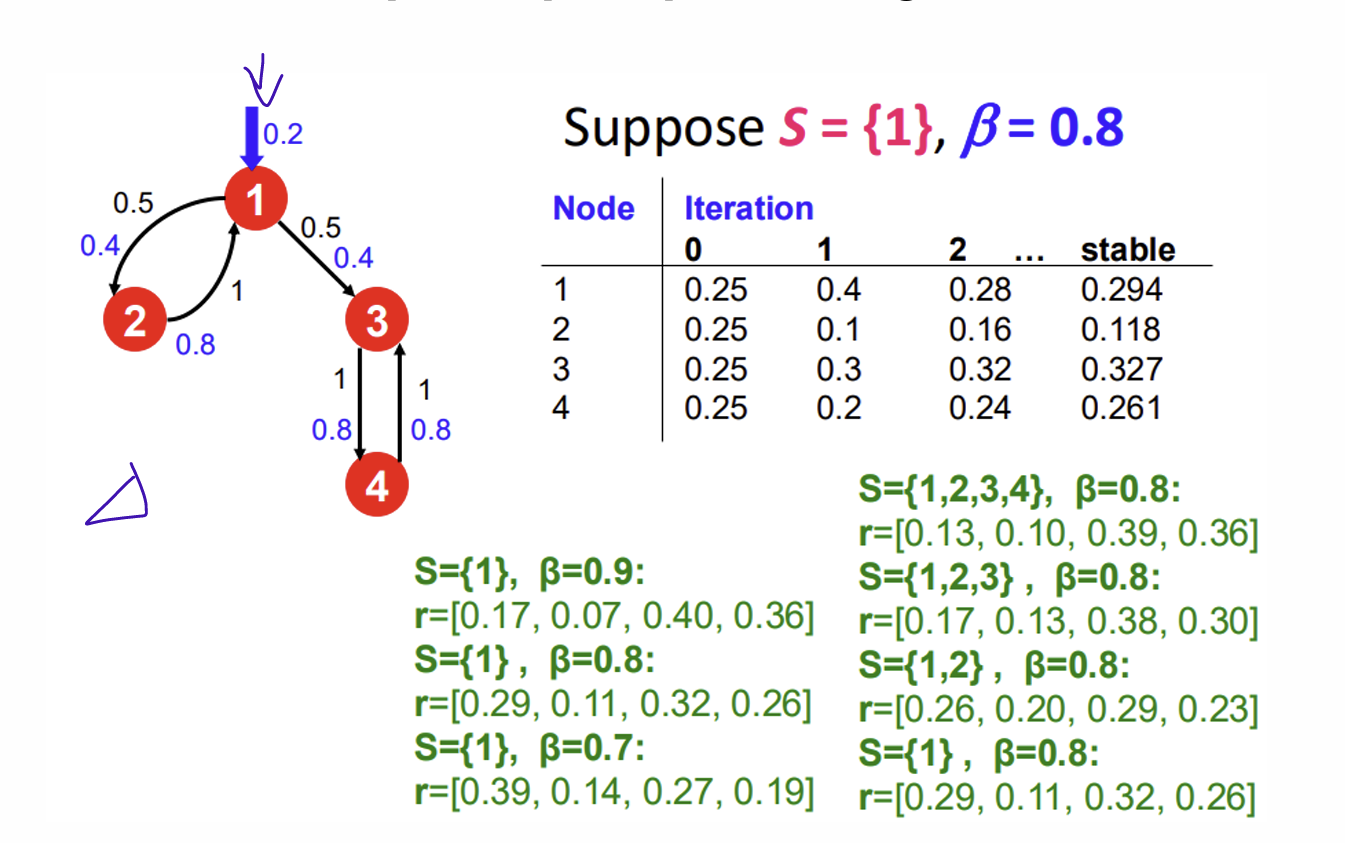
How to Compute: Topic-Specific Teleportation
idea: Bias the random walk
When teleports, pick a page from a set S
S contains only relevant pages
For each teleport set S, we get a different vector $r_s$

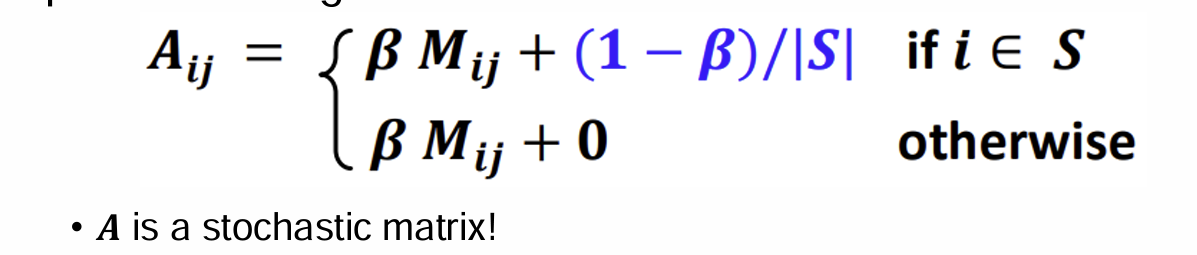
안 외워도 됨

Which topic ranking to use: user can pick, classify query into a topic, context of the query, user context