강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)

다익스트라(Dijkstra)란?

다익스트라는 BFS + 양념이라고 생각하면 된다.
즉, BFS에서 가중치라는 개념이 들어간다고 생각하면 된다.

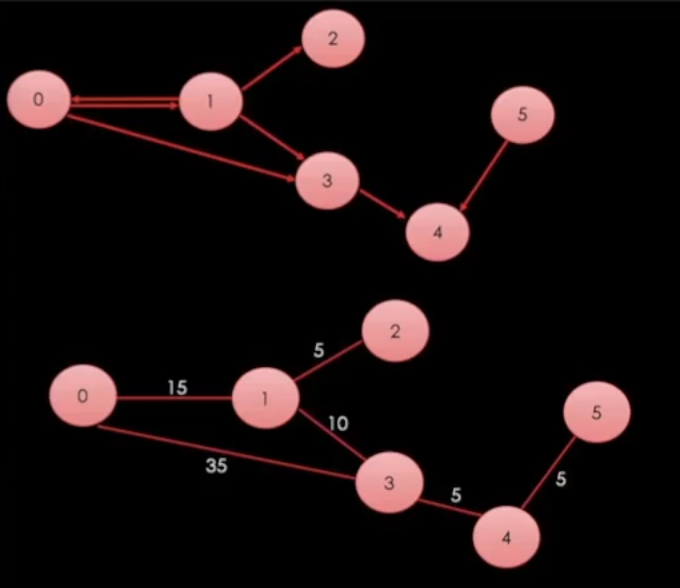
아래처럼

BFS에서는 우리가 가장 먼저 발견한 것에 접근하였다.
하지만 다익스트라는 가중치가 작은 것에 접근하는 개념이라고 볼 수 있다.
가중치는 작을 때 더 좋은 것이다.

이단 위에 그래프로 어떤식으로 다익스트라가 실행되는지 알려주겠다.
일단 0에서 시작을 한다. 0이 1과 3을 발견한다.
0->1은 15가중치를 가지고 0->3은 35의 가중치를 가진다.
먼저 1에 접근을 해서 2와 3을 찾는다.
1->2는 15+5=20의 가중치를 얻고 1->3는 15+10=25의 가중치를 얻는다.
일단 2에 접근을 하고 끝이니까 나온다. 그리고 3에 접근을 하는데..
가중치가 25와 35가 있으면 더 작은 것에 접근을 하기때문에 1->3이 접근되고 0->3은 버려진다. 이런식으로 작동이 된다고 볼 수 있다.

즉 앞에서 3을 발견하더라도 기록을 해놓지만 무조건 그 순서대로는 가지 않고
그때 내가 가진 후보중에서 베스트 케이스를 접근하는 것이다.

애도 BFS처럼 예약시스템이지만 가장 먼저 발견하는 것을 꺼내는 것이 아닌
지금 까지 내가 발견한 애들중에서 가중치가 가장 작은 애를 꺼내는 것이다.

정보가 여러가지가 들어가있는데 거기서 베스트 케이스를 뽑을 수 있는 자료구조가 무엇이 있었는가?
바로 우선순위 큐이다.

우선순위 큐는 큐이긴 큐인데 가중치(점수)에 따라서 꺼내주기 때문에 찰떡궁합이라고 볼 수 있다.

그래서 BFS에서 일반 큐를 사용하지 않고 우선순위 큐를 사용한다면 그것이 다익스트라라고 할 수 있다.

그럼 구현을 해보자

다익스트라(Dijkstra) 구현

일단 양방향으로 인접 리스트를 만들어 준다.

struct Vertex
{
	// int data;
};

vector<Vertex> vertices;
vector<vector<int>> adjacent;

void CreateGraph()
{
	vertices.resize(6);

	adjacent = vector<vector<int>>(6, vector<int>(6, -1));
	adjacent[0][1] = adjacent[1][0] = 15;
	adjacent[0][3] = adjacent[3][0] = 35;
	adjacent[1][2] = adjacent[2][1] = 5;
	adjacent[1][3] = adjacent[3][1] = 10;
	adjacent[3][4] = adjacent[4][3] = 5;
	adjacent[5][4] = adjacent[4][5] = 5;
}

양방향은 이런식으로 만들어 줄 수 있다.

그럼 이제 Dijsktra함수를 만들어보자
여기까지는 BFS와 매우 유사하다.
하지만 여기서 새로운 Struct를 만들어 준다.

struct VertexCost
{
	VertexCost(int cost, int vertex) : cost(cost), vertex(vertex) { }

	int cost;
	int vertex;
};

Vertex와 Cost를 둘 다 가지고 있는 Struct를 만들어 줄 것이다.
(나중에는 std::pair<int, int>이런식으로도 만들 수 있다고 한다)

void Dijikstra(int here)
{
	priority_queue<VertexCost> pq;
}

그리고 이런식으로 VertexCost를 받아주는 우선순위 큐를 만들어 줄 것이다.
하지만 이런식으로 만들어준다면 오류가 날 것이다.

왜냐하면 우선순위 큐는 우리가 어떠한 정보를 넣어주었을 때
대소비교를 통해서 cost가 올 위치를 정해줄 수 있는데 지금 Struct에는
대소비교 구분이 없기때문에 오류가 나는 것이다.

struct VertexCost
{
	VertexCost(int cost, int vertex) : cost(cost), vertex(vertex) { }

	bool operator<(const VertexCost& other) const
	{
		return cost < other.cost;
	}

	bool operator>(const VertexCost& other) const
	{
		return cost > other.cost;
	}

	int cost;
	int vertex;
};

그래서 operator로 이런식으로 만들어 줄 수 있다.
내부에서 const로 선언되어 있기 때문에 const를 붙혀줘야 한다.

일단 전체 코드이다.

void Dijikstra(int here)
{
	priority_queue<VertexCost, vector<VertexCost>, greater<VertexCost>> pq;
	vector<int> best(6, INT32_MAX);
	vector<int> parent(6, -1);

	pq.push(VertexCost(0, here));
	best[here] = 0;
	parent[here] = here;

	while (pq.empty() == false)
	{
		// 제일 좋은 후보를 찾는다
		VertexCost v = pq.top();
		pq.pop();

		int cost = v.cost; 
		here = v.vertex;
		
		// 더 짧은 경로를 뒤늦게 찾았다면 스킵
		if (best[here] < cost)
			continue;

		// 방문
		cout << "방문!" << here << endl;

		for (int there = 0; there < 6; there++)
		{
			// 연결되지 않았으면 스킵
			if (adjacent[here][there] == -1)
				continue;

			// 더 좋은 경로를 과거에 찾았으면 스킵
			int nextCost = best[here] + adjacent[here][there];
			if (nextCost >= best[there])
				continue;

			// 지금까지 찾은 경로중에서는 최선의 수치 = 갱신
			best[there] = nextCost;
			parent[there] = here; // 나중에 갱신될 수 있음
			pq.push(VertexCost(nextCost, there));
		}
	}
}

너무 적다보니 난잡해져서 과정 정리로 묶었다.

과정 정리

다익스트라 과정을 정리해보자면
양방향으로 연결되어 있고 가중치가 있는 그래프를 만들어준다.
그리고 VertexCost같이 정점의 가중치를 넣을 수 있는 struct를 만들어준다.
(operator를 const로 정의해야한다)

그 후 다익스트라가 실행되는데
처음으로는 우선순위 큐를 만들어준다.
템플릿 인수를 자기와 알맞게 넣주면 된다.
만약 내림차순을 하고 싶다면 기본값 그대로 내비두면 되고
오름차순을 하고 싶다면 greater을 써주면 된다.

그리고 best같은 좋은 경우를 저장해줄 수 있는 변수를 만들어준다.
그 후 BFS와 같이 parent같은 연결시켜주는 변수를 만들어준다.

그리고 우선순위 큐에 시작점을 push해주고,
시작점이니 best(가중치)는 0으로 넣어주고
parent는 자기자신이니 here을 넣어준다.

그리고 큐가 빌때까지 while문을 돌려준다.

제일 좋은 후보를 찾기위해서
우선순위 큐에 top을 넣어주고 pop을 해준다.

그 후에 cost같은 변수를 만들어서 거리값을 넣어주고
here에는 정점 정보를 넣어준다.

다음으로 더 짧은 경로를 뒤늦게 찾았다면 스킵을 시켜버린다.
best에 here가 cost보다 작으면
즉 저번값이 이번 값보다 작으면 넘긴다.

그리고 방문했다는 도장을 찍어주고 (확인용)

행렬이기에 행렬방식으로 6X6이기에 there을 for문으로 6번 돌려준다.
(예시임)

그 후 for문 안에
adjacent[here][there] == -1 즉 연결되어 있지않다면 스킵해주는 조건을 만들어 준다.

다음에는 더 좋은 경로를 과거에 찾았을 수도 있기 때문에
nextCost같은 지금까지의 거리값과 다음 한 칸의 거리값을 더 해주는 변수를 만들어주고
그 더한 총량(nextCost)가 best[there]보다 크다면 넘겨주는 코드를 짜준다.

그 후에 지금까지 찾은 경로중에서 최선의 수치는 계속 갱신이 될 수 있기 때문에
best[there] = nextCost 같이 위에 모든 시련을 이겨낸다면 갱신시켜준다.
parent도 나중에 갱신시에 바뀔 수 있기때문에
parent[there] = here 처럼 갱신할 수 있게 만들어 준다.

그 후에 우선순위 큐에 VertexCost에 nextCost와 there 즉 총 거리값과 정점을 넣어줘서 push를 해준다.

이것이 다익스트라의 순서이다.

정리

그래서 한 줄 요약을 해보자면
Dijkstra = BFS + 양념(cost)

• BFS = queue
• Dijkstra = priority_queue
  라는 것을 알 수 있다.

그래서 우리는 앞으로 가중치가 있는 상태에서 다익스트라라는 방법을 사용할 수 있다는 것이다.

그럼 우리는 BFS에서 발전된 다익스트라를 배웠다.
생각을 해보면 다익스트라 다음에는 A*이 있는데 다익스트라에서 부족한 점은 무엇이 있을까?

바로 목적지라는 개념이 없다.
다익스트라는 BFS처럼 필요없는 곳을 방문하지만 그 최단거리 부분이 실시간으로 바뀌는 것이기 때문에 아직 목적지라는 개념이 없다.

그래서 아직까지 전체맵을 검색(서치)하고 있다는 것이 단점이다.
하지만 BFS에서 나오지 않은 가중치라는 부분이 나오기 때문에 그것은 장점이라 볼 수 있다.

그래서 목적지를 아는 다익스트라가 A*알고리즘이라고 볼 수 있다.

이때까지는 길찾기를 만들 때 목적지라는 개념이 없어서 모든 맵을 탐색하고
거기서 목적지까지 parent라는 것으로 추적을 하여 이어 붙여서 만든 것이였다.

그래서 이 부분을 A*으로 고쳐볼 것이다.