강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)

BFS(breath first search)란?

BFS(breath first search)는 너비 우선 탐색이다.
그리고 BFS는 큐를 생각하면 된다. (큐로 구현이 가능하다)

그래프 만드는 것은 저번에 DFS한 것과 똑같이 만들어주면 된다. 그리고 DFS와 기본 개념은 비슷하지만 DFS는 '깊이' 우선 탐색이고 BFS는 '너비' 우선 탐색이다.

DFS가 던전에서 보스를 잡기위해 무작정 끝까지 들어가는 것이라면
BFS는 던전에서 잡몹부터 차근차근 다 처리한 후에 보스를 잡으러 가는 것과 비슷하다고 볼 수 있다.

즉, 너비 우선 탐색이란 한 칸 한 칸 차근차근 가까운 순서대로 접근하는 것이다.

일단 저번처럼

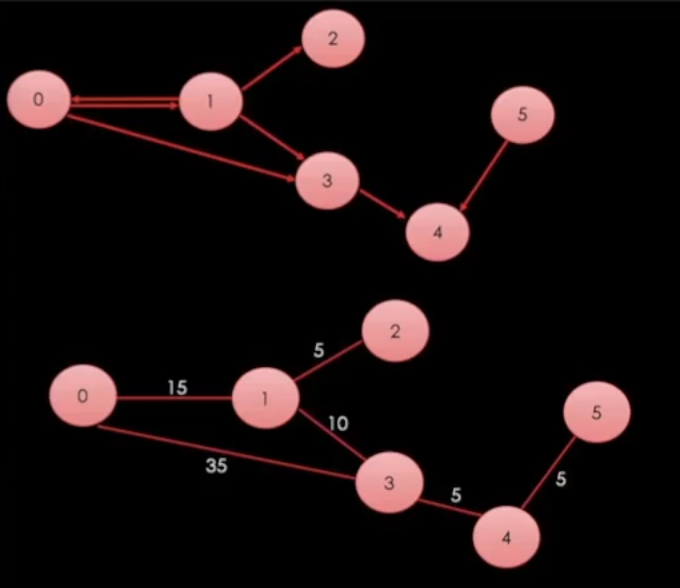
이 그래프를 사용하여서 구현해 볼 것이다.

BFS는 그냥 내가 발견한 순서대로 가면 된다.
만약 1번과 3번을 발견한다면 어떤식으로 다른걸 발견해도 무시하고 무조건 1번과 3번을 먼저 접근하는 것이다.

그리고 1번 3번이 동시에 들어와도 중요한것이 아니다. 그냥 둘 중에 무엇을 먼저 접근할지는 선택을 해주면 되는 것이다.
중요한 것은 1번 3번 무엇을 갈지는 정할 수 있지만 나머지는 나중에 된다는 것이 중요하다.

이것은 선입선출의 개념과 비슷하다. 그래서 큐를 통해서 BFS를 구현할 수 있다.

그럼 BFS를 구현해보자

BFS 구현

일단 코드부터 보자

인접 리스트

void Bfs(int here)
{
	queue<int> q;
	q.push(here);
	discovered[here] = true;

	while (q.empty() == false)
	{
		here = q.front();
		q.pop();

		// 방문 도장
		cout << "Visited : " << here << endl;

        // 인접 리스트
		int size = adjacent[here].size();
		for (int i = 0; i < size; i++)
		{
			int there = adjacent[here][i];
			if (discovered[there])
				continue;

			q.push(there);
			discovered[there] = true;
		}
	}
}

일단 큐로 예약시스템을 만들어준다.
그래서 q.push(here)로 here을 넣어준다.
그리고 우리가 사이클을 방지하기 위해서 넣어줬던 visited처럼
BFS도 "발견"하였는지의 여부를 체크해야 한다.
방문이 아닌 발견으로 용어가 바뀐다.

왜냐하면 발견한 순서대로 접근을 해야하기 때문이다.
즉 그래서 vector<bool> discovered;라는 변수를 만들어 준다.

그리고 discovered = vector<bool>(6,, false);로 초기화를 시켜준다.

위에서 큐에 push해준다는 것은 발견을 했다는 것이기 때문에
discovered[here] = true를 해준다. 즉 이제 push와 발견은 세트인 것이다.

그리고 큐가 비어있지 않을 떄까지 while문을 돌려준다.
큐가 할 것이 없다는 것은 이미 스캔을 다 끝낸 것이기 때문에 while에서 탈출한다.

일단은 here = q.front()와 q.pop();으로 방금 넣은 0을 꺼낸다.

그 다음에 방문을 하였는지 체크하고
인접한 정점들을 검색해줄 것이다. 이 부분은 DFS와 비슷하다.

일단 size만큼 for문을 돌려주고 발견을 한 곳이라면 continue를 해준다.
설명하자면 0번에서 1번 3번을 발견을 한 상태인데 1로 접근해서 2번과 3번을 발견하면 3번은 건너뛰는 것이다.
그 다음으로 예약을 해주면 된다.
큐에 there를 push해주고 발견했다고 disscovered[there] = true;를 해주면 된다.

그럼 실행을 해보면

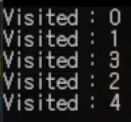
이 순서대로 방문(접근)이 되었다는 것을 알 수 있다.

큐에 접근되는 순서를 적어본다면
0이 큐에 들어오고 0을 접근을 하고 큐에서 빼면서 here에 넣음 1과 3을 발견하여서 1과 3이 큐에 들어온다. 그리고 1에 접근을 하고 큐에서 뺴면서 2와 3을 발견함 3은 발견 되었기에 2만 큐에 들어감 그리고 3에 접근을 하여 큐에서 뺴고 4를 발견해서 큐에 넣음 그리고 2번은 접근하는 데 끝이기 때문에 끝나고 4번도 접근하는 데 끝이기 떄문에 끝난다.

인접 행렬

void Bfs(int here)
{
	queue<int> q;
	q.push(here);
	discovered[here] = true;

	while (q.empty() == false)
	{
		here = q.front();
		q.pop();

		// 방문 도장
		cout << "Visited : " << here << endl;
		
        //인접 행렬
		for (int there = 0; there < 6; there++)
		{
			if (adjacent[here][there] == 0)
				continue;
			if (discovered[there])
				continue;

			q.push(there);
			discovered[there] = true;
		}
	}
}

인접 행렬로 구현해도 알고리즘 적으로 별로 바뀌는 부분은 없다.

이것도 0이면 continue하고 발견되었으면 continue하고 큐에서 넣어주는 부분은 일치한다.

그럼 이것도 DFS와 같이 모두 출력하고 싶다면

BFS ALL

void BfsAll()
{
	discovered = vector<bool>(6, false);

	for (int i = 0; i < 6; i++)
		if (discovered[i] == false)
			Bfs(i);
}

이런느낌으로 DFS와 비슷하게 만들어주면 된다.

BFS 심화

BFS는 어떤 순서로 작동할까? 하면
BFS는 너비 우선 탐색이기 떄문에 가장 가까운 곳부터 검색한다.
0->1 0->3이 맞다.

그리고 BFS는 길찾기와 어떤 관련이 있을까 생각을 해보면,
BFS에 이런저런 정보를 넣게 된다면 그 정보들을 얻어올 수 있는데

우리가 0->3으로 갔는데 그게 과연 최단거리인가를 보장할 수 있을까?
그리고 나중에 더 빠른길을 찾을 수 있을까?가 질문이 될 수 있다.

BFS는 찾을 수 없다. 왜냐하면 BFS는 너비 우선 탐색이기 때문에
가까운걸 먼저 검색하기 때문에 나중에 더 빠른걸 찾았다는 것이 있을 수가 없다.

1칸찾고 2칸찾고 이런식이기 때문에 새치기하는 경로가 나올 수가 없다.

그래서 그냥 BFS는 길찾는데 의미가 없고 여러 힌트들을 넣어줘야지 의미가 있다고 볼 수 있다.

그래서 우리가

void Bfs(int here)
{
	queue<int> q;
	q.push(here);
	discovered[here] = true;

	while (q.empty() == false)
	{
		here = q.front();
		q.pop();

		// 방문 도장
		cout << "Visited : " << here << endl;
		
        //인접 행렬
		for (int there = 0; there < 6; there++)
		{
			if (adjacent[here][there] == 0)
				continue;
			if (discovered[there])
				continue;

			q.push(there);
			discovered[there] = true;
		}
	}
}

이 코드에 두 가지 정보를 추가할 것이다.

누구에 의해서 발견되었는지에 대해서
vector<int> parent(6, -1);
시작점에서 얼만큼 떨어져 있는지?
vector<int> dist(6, -1);
이런식으로 정보를 추가한다.

그리고 처음(시작점)에는 parent[here] = here;을 통해서 자기 자신을 넣어준다.
그리고 처음(시작점)이기에 거리는 dist[here] = 0으로 해주면 된다.

그리고
예약을 하고 난 후에
parent[there] = here; there은 here에게 발견되었다는 코드를 작성하고
dist[there] = dist[here] + 1;
즉 here까지 1만큼 걸렸다면 there는 here+1의 거리를 가지고 있기때문에
dist[here] + 1이라는 코드를 dist[there]에다가 넣어준다.

그래서 즉 parent를 보면
0에서 1,3
1에서 2
3에서 4로 연결된다는 것을 알 수 있다.
5는 -1로 연결이 안된다.

dist는
0은 0
1과 3은 1
2와 4는 2
5는 -1(연결 안 됨) 이라는 것을 알 수 있다.

정리 & 마무리

그래서 DFS와 BFS는 그 자체로 의미가 있는 것이 아니라 힌트 즉 정보를 넣어서 만들어서 분석을 해서 정보를 수집한다면 의미가 더욱 의미가 있을 것이다.

그러면 이제 위에 parent와 dist를 넣었던 것 처럼
parent는 다시 돌아갈 때 얼마나 걸리는지 알 수 있어서 최단경로를 알 수 있고
dist는 거기까지 가는데 몇 번 거쳐가는지 알 수 있다는 것이다.

그리고 BFS 시간 복잡도는 DFS랑 똑같다.

다음시간에는 다익스트라를 배워볼 것인데
다익스트라는 BFS + 양념 이라고 볼 수 있다.

그리고 마지막으로 BFS = 큐 이렇게 생각을 하자.