강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)
그래프는 트리와 비슷하다. 하지만 그래프가 좀 더 범위가 넓다 라고 할 수 있다.
트리가 그래프의 일종이라고 보는 것이 좀 더 편하다.
그래프란?
그래프는 [현실 세게의 사물이나 추상적인 개념 간]의 [연결 관계]룰 표현하는 것이다.
정점(Vertex): 데이터를 표현하는데 사용한다. (사물, 개념 등)
간선(Edge): 정점들을 연결하는데 사용한다.
그래프에 예시로는 이러한 것을 볼 수 있다.
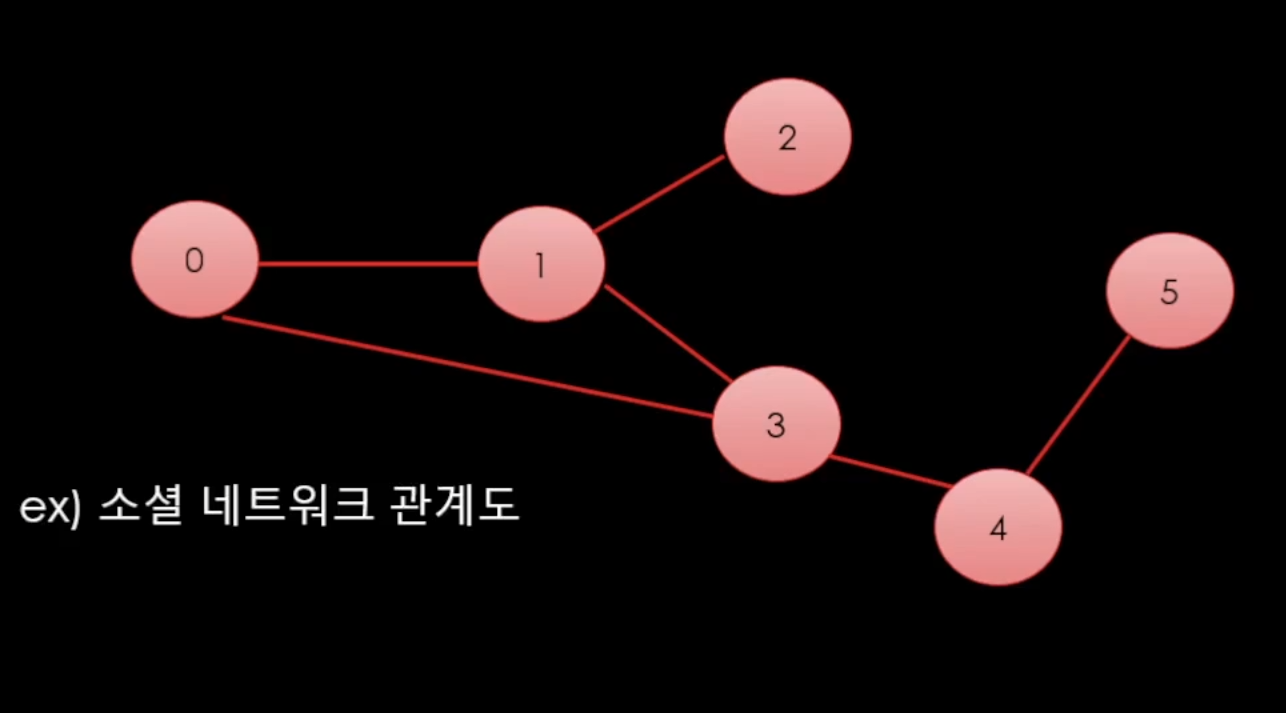
위 사진을 보면
트리와 비슷하지만 트리는 계층관계(부모, 자식)을 가지고 있고
그래프는 다 평등(형제)라고 볼 수 있다.
여기다가 추가적인 정보도 섞을 수 있다.
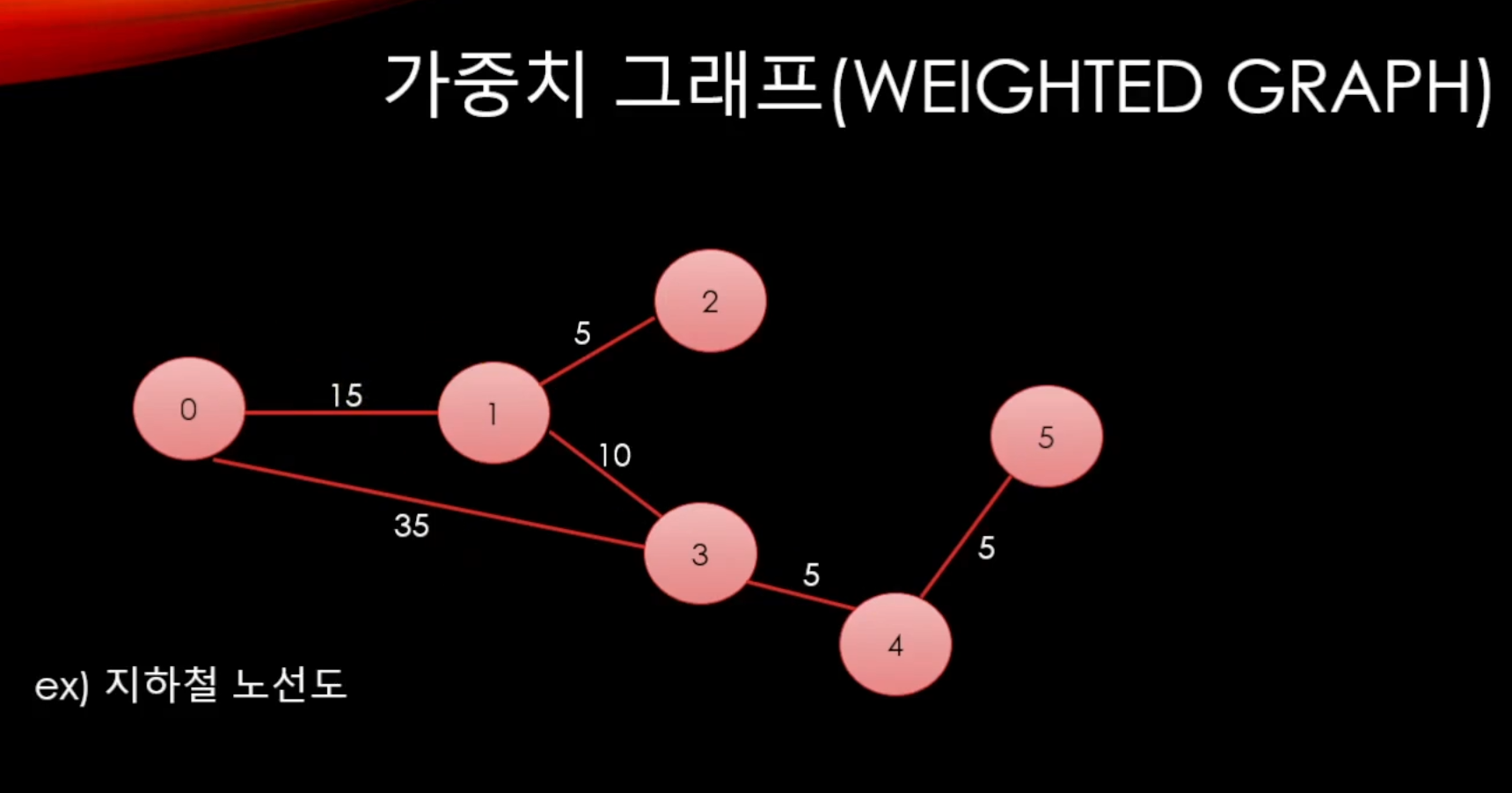
이런식으로 간선에다가 수치를 줘서 어떤 비용을 나타낼 수 있다.
만약 지하철 노선도를 만든다고 하면
지하철역을 정점으로 하고 지하철역끼리의 경로를 간선으로 표현하고 그 사이에 걸리는 시간을 간선에다가 넣어줄 수 있다는 것이다.
게임으로 본다면 물이면 느려지고 평평하면 빨라지고 돌밭이면 조금 느려지게 만들도록
가중치를 줄 수 있다.(그 가중치로 최적의 길을 판단할 수도 있을 것이다)
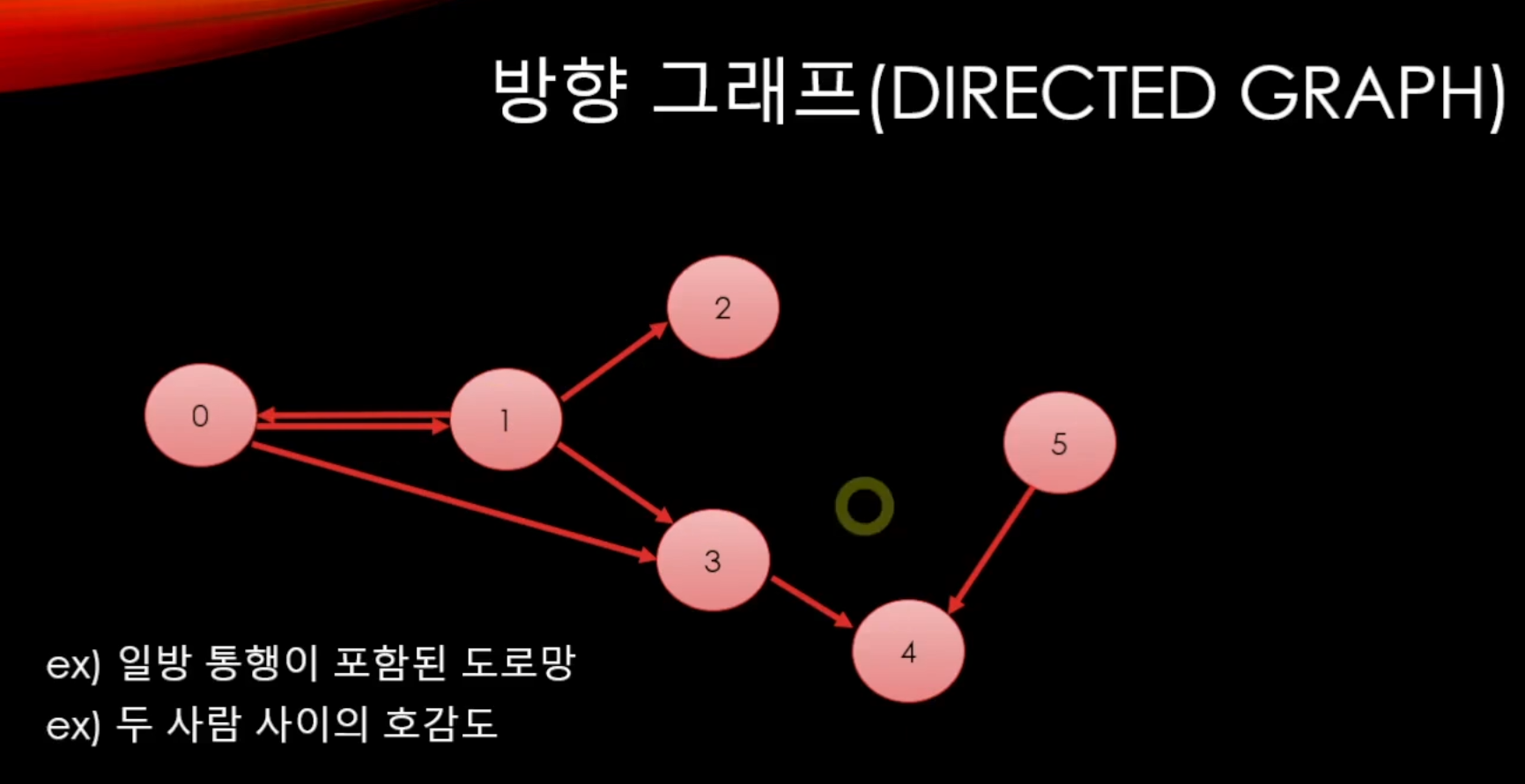
그리고 이런식으로 단방향으로도 정보를 나타낼 수 있다.
그래프는 이러한 것들을 분석하는 것이 핵심이라고 볼 수 있다.
그래프를 표현하는 법
일단 그 전에 그래프로 무엇을 만들 수 있는지 대강 알아본다면
맵 길찾기, lock이 순환되는지?(서버) 등에 사용된다.
그래프도 트리와 마찬가지고 현업에서는 거의 쓸일이 없을 것이다.
하지만 이 그래프를 공부함으로 인해서 내가 할 수 있는 것이 늘어날 것이다.
(시야가 넓어진다)
우리는 게임에서만 사용할 것이기에 길찾기 위주로 알아 볼 것이다.
잠깐!
vector의 resize와 reserve의 차이를 알아보자
vector의 resize는 size와 연관이 있고
vector의 reserve는 capacity와 연관이 있다.
vector.resize(6)를 하게 된다면 v.push_back(Vertex()); 이 구문이 6개 들어간 것과 비슷하다.
즉 실제 데이터 개수가 6개가 되었다. 라고 볼 수 있다.
vector의 reserve는 아직 데이터는 없지만
나중에 이사하는 비용을 줄이기 위해서 capacity(용량)을 늘려서 영역을 확보해놓는 것이다.
그리고 vector에는 선언과 동시에 vertor<Vertex*> v(6) 이런식으로 resize를 해줄 수 있다.
이것도 방식이 여러가지가 있는데
vector<int> v2(10, -1) 이런식으로 선언을 하게 된다면 -1로 데이터 10개를 넣어주는 것이다.
그리고 vector<int> v3(1, 2, 3, 4, 5, 6) 이런식으로 직접적으로 초기값을 넣어줄 수 있다.
구현
만약 이 그래프를 구현하게된다면 처음에는 이런식으로 구현해볼 수 있다.
#include <iostream>
using namespace std;
#include <vector>
void GreateGraph_1()
{
struct Vertex
{
// int data;
vector<Vertex*> edges;
};
vector<Vertex> v(6);
v[0].edges.push_back(&v[1]);
v[0].edges.push_back(&v[3]);
v[1].edges.push_back(&v[0]);
v[1].edges.push_back(&v[2]);
v[1].edges.push_back(&v[3]);
v[3].edges.push_back(&v[4]);
v[5].edges.push_back(&v[4]);
// Q) 0번->3번 연결이 되어 있는가?
bool connected = false;
int size = v[0].edges.size();
for (int i = 0; i < size; i++)
{
Vertex* vertex = v[0].edges[i];
if (vertex == &v[3])
{
connected = true;
}
}
}하지만 이런식으로 구현한다면 그래프는 트리처럼 계층관계를 가지고 있는 것도 아니기 때문에 그래프를 빠르게 판별할 수 없다.
그래서 직관적이지만 보통 이런식으로는 만들지 않는다.
만드는 방법은 두 가지가 있는데 인접 리스트와 인접 행렬이다.
인접 리스트
먼저 인접 리스트로 구현을 해보자
인접 리스트는 실제로 연결된 애들(데이터)'만' 넣어주는 것이다.
구현을 하면 이런식으로 구현할 수 있다.
// 인접 리스트 : 실제 연결된 애들'만' 넣어준다
void CreateFraph_2()
{
struct Vertex
{
int data;
};
vector<Vertex> v(6);
vector<vector<int>> adjacent;
adjacent.resize(6);
//adjacent[0].push_back(1);
//adjacent[0].push_back(3);
adjacent[0] = { 1, 3 };
adjacent[1] = { 0, 2, 3 };
adjacent[3] = { 4 };
adjacent[5] = { 4 };
}이런식으로 vertex(정점)은 위처럼 관리하고 연결여부는 아래처럼 관리 할 수 있다.
2차원 배열을 사용하여서 vector안에 vector가 무엇을 가지고 있는지 가르치게 만들 수 있다.
즉 이런식으로 인접한 데이터만 가지고 있기때문에 인접 리스트이다.
그렇기에 2번과 4번은 진짜로 아무 데이터도 가지고 있지않고 인접한 0, 1, 3, 5번만 데이터를 넣어주는 것이다.
그럼 저기서 Q) 0번->3번 연결이 되어 있는가? 라는 질문을 하면
bool connected = false;
int size = adjacent[0].size();
for (int i = 0; i < size; i++)
{
int vertex = adjacent[0][i];
if (vertex == 3)
{
connected = true;
}
}이런식으로 짜줄 수 있다.
여기서 생각해볼 수 있는 것이 그래프를 사용할 때 장단점이 갈리게 된다.
정점이 100개 일때
지하철 노선도랑 페이스북 친구가 있다면
지하철 노선도는 -> 서로 드문 드문 연결되어있다.
하지만 페이스북 친구는 -> 만약 핵인싸라면 서로 뺵뺵하게 연결되어있을 수 있다.
그래서 위에 두 상황에 대해서 어떤지에 대해 고려를 해봐야한다.
인접리스트는 실제로 연결된 애들'만' 넣어주기 때문에
서로 드문 드문 연결되있는 쪽에 이점이 있을 것이다.
(나랑 연결된 애들만 넣어주면 되서)
만약에 정점이 100개이고 나랑 연결 된 애들이 많다고 하면 인접리스트는 각각 100개씩 넣어줘야 하기때문에 효율적인지는 좀 애매하다고 볼 수 있다.
그래서 이러한 경우에는 인접 행렬이 더 좋을 것이라고 예측해볼 수 있다.
인접 행렬
그럼 인접행렬을 구현해보자
인접행렬은 연결된 데이터 목록을 행렬로 관리하는 것이다.
행렬은 배열을 만들어서 2차원으로 관리한다고 생각하면 된다.
[x][x][x][x][x][x]
[x][x][x][x][x][x]
[x][x][x][x][x][x]
[x][x][x][x][x][x]
[x][x][x][x][x][x]
[x][x][x][x][x][x]
이런식으로 표를 만드는 개념이다.

이 그래프를 표현한다면
[x][O][x][O][x][x]
[O][x][O][O][x][x]
[x][O][x][x][x][x]
[O][O][x][x][O][x]
[x][x][x][O][x][O]
[x][x][x][x][O][x]
이런식으로 표현해줄 수 있다.
그럼 이거를 코드로 표현해본다고 생각하면
vector<vector<bool>> adjacent 이런식으로 짜줄 수 있다.
그리고 모든 구간을 false로 초기화 하고 싶다고 하면은
vector<vector<bool>> adjacent(6, vector<bool>(6, false)) 이런식으로 초기화 해줄 수 있다.
둘이 따로 한줄로 보면 이해하기 편할 수 있다.
vector<bool>(6, false);
vector<vector<bool>> adjacent;
// 두개를 합친다고 생각하자
vector<vector<bool>> adjacent(6, vector<bool>(6, false));한마디로 2차원으로 만드는 것이다.
남은 부분은 원하는 부분만 골라서 true로 바꿔주면 된다.
adjacent[0][1] = true;
adjacent[0][3] = true;
adjacent[1][0] = true;
adjacent[1][2] = true;
adjacent[1][2] = true;
adjacent[3][4] = true;
adjacent[5][4] = true;이런식으로 말이다.
인접 행렬과 인접 리스트의 차이점
이러면 인접 행렬과 인접 리스트의 차이점을 알게될 수 있다.
인접 리스트는 연결된 값 자체를 넣어주는 개념이고
인접 행렬은 그냥 표하나를 만들어서 모든 애들의 값이 할당되어 있기때문에 표를 참고하면 되는 것이다.
그럼 여기서 Q) 0번->3번 연결이 되어 있는가? 라는 걸 인접 행렬로 구현시켜 본다면
표로 0번이랑 3번이 연결되어 있는가를 표현하고 있는 것이다.
그래서
adjacent[from][to]이게 true인지 false인지만 확인을 하면 되는 것이다.
이것이 행렬을 이용한 그래프 표현이다.
그래서 인접 행렬은 메모리 소모가 심하지만, 빠른 접근을 할 수 있다는 걸 알 수 있다.
코드로 구현해보면
bool connected = ajacent[0][3]; 이런식으로만 하면 찾을 수 있다.
정리
이 부분은 정리와 복습을 하면서 이해를 하는 것이 필요하다.
결국에 중요한 것은 그래프를 표현하는 2가지 방식이 있고 그 두가지는
내가 연결된 번호들만 가져오는 인접 리스트가 있고
아니면 그래프를 행렬로 관리하는 인접 행렬이 있다는 것이다.
이것만 이해한다면 뒤에 나오는 부분은 직관적이긴 하다.
만약 간선에 대한 번호까지 만든다면 bool대신 int를 넣어서 끊겨있는 것은 -1
연결되있는 수치들을 넣어주면 될 것이다.

만약 이 그래프를 구현해본다면
vector<vector<int>> adjacent2 =
{
{ -1, 15, -1, 35, -1, -1 },
{ 15, -1, +5, 10, -1, -1 },
{ -1, +5, -1, -1, -1, -1 },
{ 35, 10, -1, -1, +5, -1 },
{ -1, -1, -1, +5, -1, +5 },
{ -1, -1, -1, -1, +5, -1 },
};이런식으로 구현할 수 있다.
이런식으로 구현한다면 -1로 확실히 끊어졌는지 알 수 있고 연결된 간선에는 얼마의 가중치가 있는지도 알 수 있다.
여기서 또 다른 질문이 나올 수 있는데
우리가 어떤 백터, 리스트, 우선순위 큐 등을 사용한다면 전체 순회를 하는 부분이 중요할 것이다.
그래야지 모든 데이터를 스캔할 수 있기 때문이다.
백터는 쭉 순회하면 되고 트리는 재귀함수로 하면 됐다.
그래프는 재귀함수로 할 수 있을까? 분명 이상한 부분이 있을 것이다.
생각보다 그래프는 쭉 순회하는거 조차 쉽지않다는 것을 알 수 있다.
그래서 우리는 다음에 DFS와 BFS를 배울 것이다.
이것을 배울 때 외우는 것이 아니라 왜 필요한지를 알아야 한다.
그럼 생각해보면 DFS나 BFS같은 규칙(정책)이 없다면 그래프를 한 번 다 스캔하는 것도 쉽지 않다는 것을 알 수 있다.
그래서 우리가 그래프를 공부하면
그래프가 무엇인지 이해하고
그래프를 표현하는 방식이 두 가지가 있다는 것을 이해하고
그 다음순서로 내가 어떤식으로 그래프 전체를 스캔 할 수 있을까?라는 고민을 하는게 순서라고 볼 수 있다.
정리하다보니 엄청 길어졌는데 오늘도 많은 것을 배운 것 같다.