강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)
DFS (depeth first search)란?
DFS (depeth first search)는 깊이 우선 탐색이다.
깊이라는 것은 우리가 시작점에서 얼마나 파고 들 것인가? 이다.
일단 그래프는 트리와 다르게 시작점이라는 개념이 없어서 시작점을 정해줘야 한다.
우리는 오늘 이 그래프를 기준으로 공부해 볼 것이다.
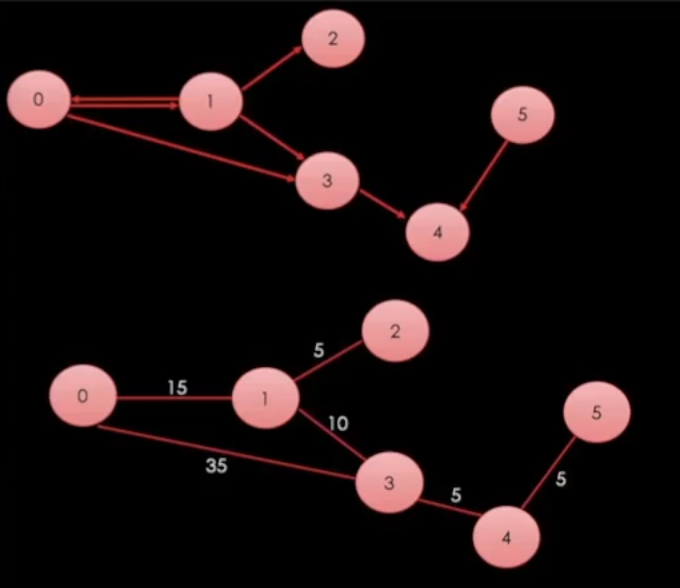
DFS는 어느쪽으로 가든 끝까지 들어간다고 보면 된다.
0 -> 1 -> 2
이런식으로 말이다.
그럼 어떤식으로 코드로 만들어야 할까 생각을 해보면
DFS는 무조건 '깊이'들어가야 하기때문에 재귀함수를 사용하면 구현할 수 있을 것 같다는 생각이 들 수 있다.
트리와 비슷하지만 트리는 다시 돌아올 수가 없었다. (트리는 단방향)
그래서 트리와 굉장히 유사하게 만들데! 방문한 곳을 다시 안가도록 만들어줘야 하는 것이다.
그럼 구현을 해보자
DFS 구현
struct Vertex
{
//int data;
};
vector<Vertex> vertices;
vector<vector<int>> adjacent;일단 이런식으로 Vertex와 인접 목록(adjacent)을 만들어준다.
그럼 우리는 그래프를 인접 리스트나 인접 행렬로 만들어 줄 수 있다.
일단 인접 리스트로 먼저 만들어보자
인접리스트
void CreateGraph()
{
vertices.resize(6);
//인접 리스트
adjacent = vector<vector<int>>(6);
adjacent[0] = { 1, 3 };
adjacent[1] = { 0, 2, 3 };
adjacent[3] = { 4 };
adjacent[5] = { 4 };
}이런식으로 인접 리스트를 만들어준다.
그리고 DFS 함수를 만들어야 하는데
함수를 만들 때 주의 해야할 점이 있다.
내가 어디까지 방문을 하였는지 여부를 추적해야 한다.
그래서 방문한 목록을 추척하기 위한 배열인 visited함수를 만들어준다.
// 내가 방문한 목록
vector<bool> visited;그리고 main함수에 visited = vector<bool>(6, false); 이런식으로 다 false로 초기화 해준다.
그래서 이 변수로 방문할 때마다 true로 바꿔서 체크를 해줄 것이다.
일단 구현한 것을 먼저 보여주겠다.
void Dfs(int here)
{
visited[here] = true;
cout << "Visited : " << here << endl;
// 인접한 길을 다 체크 해서
// 인접 리스트 O(V+E) V는 정점 개수 E는 간선의 총 개수
const int size = adjacent[here].size();
for (int i = 0; i < size; i++)
{
int there = adjacent[here][i];
if (visited[there] == false)
Dfs(there);
}
}그럼 일단 먼져 방문도장을 찍어준다.
visited[here] = true; 이런식으로 true가 되도록 찍어준다.
그리고 인접한 길을 다 체크해준다.
const int size = adjacent[here].size();이런식으로 adjacent[here]의 사이즈를 받아주고
for문으로 하나씩 하나씩 순회를 해준다.
그 다음에 there에 adjacent[here][i]를 꺼내서 넣어준다.
즉 0번에는 1번과 3번이 연결되어 있기 때문에 1번과 3번이 들어온다.
그리고 이제 연결이 되있지만 이미 방문을 하였는지는 잘 모르기 때문에
if (visited[there] == false) visited[there]이 false라면 방문이 안된 곳이기에 Dfs(there);로 Dfs를 호출해준다..
양방향으로 만드는 것과 단방향으로 만드는 것에는 차이가 있지만 지금은 단방향으로 만들었다 .

여기서 애매한 내용이 있을 수 있는데 0에서 3으로 간 것일까? 1에서 3으로 간 것일까? 이다.
0에서 1로 가는게 맞다. 왜냐하면 처음에 Dfs(1)과 Dfs(3)이 호출이 되지만,
Dfs(1)이 먼저 실행되어 Dfs(2)와 Dfs(3)을 호출하여 visited가 true가 되고
다시 돌아와서 Dfs(3)가 호출이 된다면 if문에 걸려서 실행되지 못한다는 것을 알 수 있다.
그리고 만약에 DFS를 재귀함수를 사용하지 않고 구현하게 된다면 무엇으로 구현할 수 있을까?
바로 Stack으로 구현할 수 있다.
이 부분은 면접에 나올 수 있기 때문에 DFS = 재귀함수 = Stack이라고 보면 된다.
하지만 굳이 스택으로 만들어 볼 필요는 없다고 본다.
DFS를 스택으로 만들 수 있다는 것만 기억하자.
인접행렬
만약 인접행렬 방식으로 DFS를 구현한다고 하면
void CreateGraph()
{
vertices.resize(6);
// 인접 행렬
adjacent = vector<vector<int>>
{
{ 0, 1, 0, 1, 0, 0 },
{ 1, 0, 1, 1, 0, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 1, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 1, 0 }
};
}이런식으로 인접행렬로 그래프를 만들어준다.
그리고 DFS함수를 구현하면 된는데 인접리스트와 코드가 달라진다.
void Dfs(int here)
{
visited[here] = true;
cout << "Visited : " << here << endl;
// 인접 행렬 O(V^2) V는 정점 개수
for (int there = 0; there < 6; there++)
{
// 길은 있는지
if (adjacent[here][there] == 0)
continue;
// 아직 방문하지 않은 곳에 한해서 방문
if (visited[there] == false)
Dfs(there);
}
}일단 인접 리스트는 연결된 것만 가지고 있었기 때문에 사이즈를 받아서 for문을 돌릴 수 있었지만 인접 행렬은 모든 부분 (연결 된 곳, 연결이 안 된 곳)을 가지고 있기때문에 개수만큼 there로 for문으로 돌려줘야 한다.
그리고 일단 길이 있는지 판별하기 위해서 adjacent[here][there] == 0이면 continue를 시켜준다.
그리고 방문하지 않은 곳인지 visited[there] == false로 판별을 하여서
Dfs를 호출한다.
그런데 여기서 이상한 점을 발견할 수 있다.
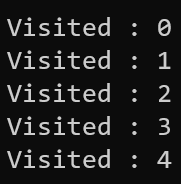
과연 모든점을 방문하였을까? 하고 보면 5번이 없다.
그래프는 다 연결되어 있을 수는 없기때문에 이럴 수가 있다.
4번에서 5번으로 가는 길이 없기 때문에 출력되지 않은 것이다.
그래서 이렇게 0번으로 스캔을 했는데 5번이 없다? 그러면 5번은 연결이 되어있지 않다는 정보를 알 수 있다.
그래도 목적 자체가 모든 정점들을 한 번씩 출력시키고 싶었던 것이라면 이런식으로 구현 하면 된다.
DFS ALL
void DfsAll()
{
visited = vector<bool>(6, false);
for (int i = 0; i < 6; i++)
{
if (visited[i] == false)
{
Dfs(i);
cout << "구분" << endl;
}
}
}이런식으로 visited를 false로 초기화 시켜주고
for문 안으로 들어와서 방문했는지 체크를 해주고 방문을 하지 않았다면 들어가서
Dfs()함수를 실행시켜주고 "구분"를 출력해주면 된다.
이러면 "구분"은 2번 출력이 되는 것을 볼 수 있다.
5번 전까지는 다 연결되어 있기 떄문에 한 번에 4번까지 출력시키고 "구분"이 한 번 나오고
if로 1번 2번 3번 4번을 걸러준뒤에 5번에 진입하였을 때 방문을 하지 않았기 때문에 Dfs함수로 들어가서 5번을 출력해준 뒤에 "구분"을 출력해주고 끝이 난다고 볼 수 있다.
시간복잡도
정점 개수를 V라고 하고
간선 개수는 E라고 한다.
인접 행렬의 시간 복잡도를 살펴보자.
void Dfs(int here)
{
visited[here] = true;
cout << "Visited : " << here << endl;
// 인접 행렬 O(V^2) V는 정점 개수
for (int there = 0; there < 6; there++)
{
// 길은 있는지
if (adjacent[here][there] == 0)
continue;
// 아직 방문하지 않은 곳에 한해서 방문
if (visited[there] == false)
Dfs(there);
}
}정점을 무조건 한 번 방문하기 때문에 일단 V가 되고
인접 행렬을 이용하여 주변에 있는 것들을 검색할 것이기 때문에
각 정점마다 한 번씩 접근하는 것은 맞지만 for문을 돌아서 인접한 것들을 체크하기 떄문에 시간 복잡도는 O(V^2)이라고 볼 수 있다.
정리하면
정점을 무조건 한 번 방문해서 V
정점개수만큼 for문을 돌리기 때문에 V
즉 V^2이다.
인접 리스트의 시간 복잡도를 살펴보자
void Dfs(int here)
{
visited[here] = true;
cout << "Visited : " << here << endl;
// 인접한 길을 다 체크 해서
// 인접 리스트 O(V+E) V는 정점 개수 E는 간선의 총 개수
const int size = adjacent[here].size();
for (int i = 0; i < size; i++)
{
int there = adjacent[here][i];
if (visited[there] == false)
Dfs(there);
}
}인접 리스트는 V는 인접행렬과 같이 모든 정점마다 한 번씩 방문하기 때문에 V이고
E는 정점에 연결된 간선이 몇 개 인지는 모르지만, 끝났을 때 간선을 한 번씩 검사하기 때문에
인접 리스트의 시간 복잡도는 O(V+E)라고 볼 수 있다.
그럼 인접 리스트와 인접 행렬중에 누가 더 빠를까?
둘 중 누구라고 말을 할 수가 없다.
간선이 모든 정점에 연결이 되어 있다면 E이 자체로도 V^2가 될 수 있기 때문이다.
그래서 그래프가 빽빽하게 되어있다면 인접 행렬이 좀 더 좋고
그래프가 드문 드문하게 되어있다면 E가 적기때문에 인접 리스트가 좋을 것이다.
정리 & 마무리
사실 DFS가 BFS보다는 할 수 있는 영역이 더 많다.
끊겨있는지도 알 수 있고, 사이클도 도는지 체크를 할 수 있다.
DFS의 개념은 당연히 알아야하고 이 DFS로 파생되는 것이 엄청 많기 때문에 배우면 좋긴하지만 우리는 목표가 길찾기 이기 때문에 BFS가 더 중요하다고 할 수 있다.