딥러닝 기본

이번 강에서는 딥러닝의 기본에 대하여 학습을 진행했다.

00. 학습 내용

• Deep Learning에 대한 간단한 Preview에 대하여 학습
• Multi-Layer Perceptron에 대하여 학습

01. Deep Learning Preview

• Deep Learning의 주요 요소 4가지는 다음과 같다.
  • Data
    • Deep Learning은 데이터를 기반한 문제 해결 방법이다.
    • 예를 들어 우리가 고양이와 강아지를 분류하는 문제를 푼다고 하면 고양이와 강아지의 이미지가 필요할 것이고, 날씨를 예측하고자하면 과거의 날씨 정보가 필요할 것이다.
    • 이렇듯 Deep Learning에서는 우리가 해결하고자 하는 문제에 적합한 Data가 필요하다.
  • Model
    • Deep Learning 에는 AlexNet, ResNet, Transformer, AutoEncoder, GAN 등 다양한 Model Architecture 들이 존재한다.
    • 각 Model Architecture 마다 잘 풀 수 있는 문제가 다르기 때문에 우리가 해결하고자 하는 문제에 맞는 적절한 Model Architecture를 만드는 것이 중요하다.
  • Loss Function
    • Loss Function은 Model을 학습시키는 방법이다.
    • 우리가 해결하고자 하는 문제는 어떠한 함수로써 존재할 것이다.
    • 우리의 목표는 그 함수를 근사할 수 있는 함수를 만드는 것인데, 근사한 함수를 만들기 위해서는 모델에게 정확한 목적을 알려줘야 한다.
    • 따라서 우리의 Task에 맞게 적절한 Loss Function을 설정함으로써 우리 모델이 문제 해결을 위한 함수에 근사한 함수를 만들 수 있을 것이다.(MSE, CE, MLE 등의 다양한 Loss Function)
  • Algorithm
    • Deep Learning에는 모델의 일반화 성능을 높이기 위한 다양한 최적화 기법들이 존재한다.(Adam, Dropout, Weight Decaym, MixUp, Ensemble 등등)

02. Multi-Layer Perceptron

• Neural Network는 비선형 변환이라고 불리는 Affine 변환을 쌓아서 만든 하나의 근사화된 함수라고 볼 수 있다.(우리의 문제를 해결해주는 하나의 근사화된 함수)

• 하나의 선형 Model을 예를 들면, 우리는 위와 같이 MSE Loss를 바탕으로 오차를 구하고, 구해진 오차를 바탕으로 각 파라미터의 편미분을 통해서 기울기를 구하고, 구해진 기울기로 오차가 감소하는 방향으로 파라미터를 업데이트 하면서, 우리의 문제를 해결할 수 있는 하나의 함수를 근사화 한다.

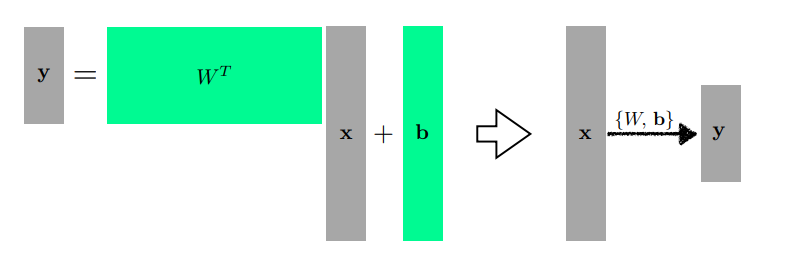
• 다차원일 때도 위 처럼 행렬을 바탕으로 우리는 문제를 해결할 수 있다($y = W^{T}x + b$). $W^{T}$를 하나의 operation 으로 본다면 위의 식은 어떠한 데이터를 새로운 space 상에서 맵핑 시키는 과정이라고 볼 수 있다.(맵핑을 시킨다는 것은 결국 어떠한 하나의 근사화된 함수를 찾는 것이라고 볼 수 있음)

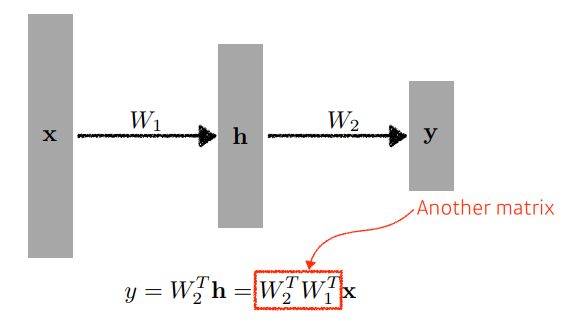
• 그러면 $W^{T}$를 계속 쌓으면 되는 것일까? 아니라고 할 수 있다. $W^{T}$를 계속 쌓으면 결국에는 그냥 크기가 다른 $W^{T}$에 변환만 일어나기 때문에 모델의 표현력이 제한될 수 있다.

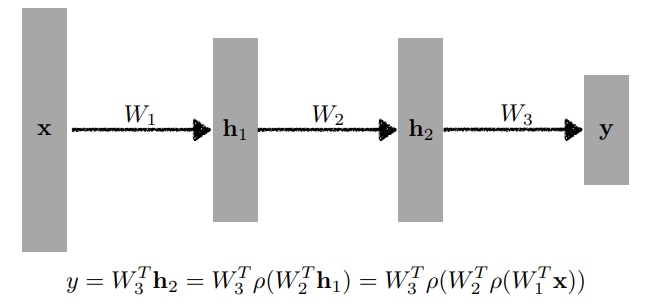
• 따라서 우리에게는 위와 같이 활성화 함수를 거쳐서 $W^{T}$를 계속 쌓아나가는 것이 중요하며, 위처럼 점점 깊어지는 Model을 바로 Multi-Layer Perceptron 라고 부른다.
• 즉, 활성화 함수는 모델의 표현력을 높이기 위한 방식이라고 볼 수 있고, 이는 비선형성이라고도 한다. 또한 비선형성이란 선형이 아닌 연산으로 중첩과 동질성을 만족하지 않는 것을 의미한다. 비선형성을 통해서 새롭게 맵핑 되는 데이터들 간의 거리에 변형이 가해져서 선형으로 분리할 수 있는 공간으로 데이터가 맵핑이 될 수 있게 되어 모델이 표현력이 높아지는 것이다.

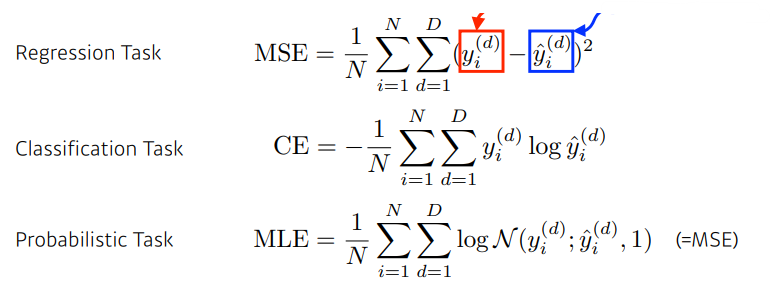
• 우리는 각각의 Task에 맞는 Loss를 쓰면서 우리가 원하는 근사화된 함수를 얻을 수 있다. (주어진 Loss 말고도 다양한 Loss를 사용할 수 았음)

• universal Approximation Theorem 에 따르면 1개의 함수로도 충분히 많은 함수를 근사화 할 수 있다고 한다. 이 이론에 기초하면 굳이 활성화 함수가 없어도, 레이어를 깊게 쌓지 않아도 충분히 우리가 원하는 함수를 근사화 할 수 있다고 말할 수 있다. 하지만 이 이론은 실제와는 맞지 않다고 볼 수 있으며, 이 이론을 단순히 Neural Network에 대입하게 되면 어떠한 Neural Network는 충분히 많은 함수를 근사화 할 수 있다는 말이 된다. 따라서 표현력이 극대화된 하나의 Neural Network는 우리가 근사화 하고 싶은 하나의 함수를 만들 수 있다.