Model Sparsity Can Simplify Machine Unlearning(Jia et al.,NeurIPS23)

이휘영·2024년 3월 9일
literature_reviewunlearning

Unlearning Literature Review

목록 보기
2/5

Model Sparsity Can Simplify Machine Unlearning(Jia et al.,NeurIPS23)

요약

  • Model Pruning을 Unlearning에 도입하였을 때 더 효과적이다.
  • Pruned Model을 Unlearn하는 방법, 또는 weight 크기에 대한 l1-norm을 unlearning loss에 추가해 pruning의 효과를 주는 두 가지 방법 제안

Unlearning Method

  • Fine-tuning (FT)
    • θo\theta_o에서 Dr\mathcal{D}_r만으로 fine-tuning하였을 때, Df=D\Dr\mathcal{D}_f=\mathcal{D}\backslash{D}_r에 대한 catastrophical forgetting을 이용하는 방법
  • Gradient ascent (GA)
    • θt+1←θt+λ∇θtℓ(hθ(x),y),(x,y)∼Dfθ_{t+1} ← θ_t + λ∇_{θ_{t}}ℓ(h_θ(x), y), (x, y) ∼ \mathcal{D}_f의 방법으로 forget class에 대한 classification loss를 최대화하는 방향으로 파라미터를 업데이트하는 방법
  • Fisher forgetting (FF)
    • θu\theta_u와 θo\theta_o의 차이가 Gaussian distribution을 따르는 확률변수 하나로 설명될 수 있다는 assumption에 기반함. 즉 θu=θo+α14F14n\theta_u=\theta_o+\alpha^{\frac{1}{4}}F^{\frac{1}{4}}n where n∼N(0,1)n\sim \mathcal{N}(0,1), F는 Fisher Information matrix(log⁡p(θo,x,y)\log p(\theta_o,x,y)의 θo\theta_o에 대한 second deriviative의 기댓값, (x,y)∼Dr(x,y)∼ D_r)
  • Influence unlearning (IU)
    • Original Model과 Unleared Model의 차이 θu−θo\theta_u-\theta_o를 어떠한 influence function으로 설명하고자 하는 접근
    • Proposed Influence Function
      Δ(w):=θ(w)−θo≈H−1∇θL(1N−w,θo)\Delta(\mathbf{w}) := \theta(\mathbf{w}) - \theta_o \approx \mathbf{H}^{-1} \nabla_{\theta} L\left(\frac{1}{N} - \mathbf{w}, \theta_o\right)

이 때 w는 크기 N의 0 또는 1로 이루어진 벡터로, forget set의 loss를 마스킹하는 목적으로 이용된다.
θ(w)\theta(\mathbf{w})는 θ\theta에 w가 적용된, 즉 retrained model을 의미

L(w,θ)=∑i=1N[wili(θ,zi)],\mathbf{L(w,}\theta)=\sum_{i=1}^{N} \left[ w_i l_i(\theta, z_i) \right], 따라서 forget set을 제외한 loss의 합

위 proposition의 유도과정은 다음과 같다.

이 때 Hessian의 계산이 매우 비싸므로 WoodFisher 근사를 적용하여 구한다.

Sparsity-Aided Machine Unlearning

Motivation

  • GA를 활용하여 Unlearning 한다고 하였을 때, 우리는 N개의 훈련 데이터로 학습된 모델 θ^N\hat\theta_N에 대한 forget point x^i\hat{x}_i의 loss의 gradient ∇θL(θ^N,x^i)\nabla_\theta L(\hat\theta_N, \hat{x}_i)를 θ^\hat\theta에 더한다. (정확히 그대로 더하지는 않지만)
  • 그러나 학습과정에서 x^i\hat{x}_i로 인해 모델이 업데이트 된 양은 ∇θL(θ^i−1,x^i)\nabla_\theta L(\hat\theta_{i-1},\hat{x}_i)이므로 위와 다르다.(이 때 θ^i−1\hat\theta_{i-1}은i−1i-1번째 데이터 포인트까지 학습한 모델의 파라미터)
  • 따라서 forget point x^i\hat{x}_i에 의한 모델의 업데이트 정도를 최종 상태, 또는 초기 상태의 모델에 대해 deterministic하게 구할 필요가 있다.

Expanding SGD (Thudi et al)

Single step SGD update (w0 to w1)을 다음과 같이 표현할 수 있다.

W1=W0−η∂L∂W∣W0,x^0,W_1 = W_0 - \eta \left. \frac{\partial \mathcal{L}}{\partial W} \right|_{W_0, \hat{x}_0},

두 번째 업데이트는 다음과 같다.

W2=W0−η∂L∂W∣W0,x^0−η∂L∂W∣W1,x^1,W_2 = W_0 - \eta \left. \frac{\partial \mathcal{L}}{\partial W} \right|_{W_0, \hat{x}_0} - \eta \left. \frac{\partial \mathcal{L}}{\partial W} \right|_{W_1, \hat{x}_1},

위 식의 두 번째 항을 W0W_0에 대해 구하기 위해 아래와 같이 근사할 수 있다.

W2≈W0−η(∂L∂W∣W0,x^0+∂L∂W∣W0,x^1+∂2L∂W2∣W0,x^1(−η∂L∂W∣W0,x^0)),W_2 \approx W_0 - \eta \left( \left. \frac{\partial \mathcal{L}}{\partial W} \right|_{W_0, \hat{x}_0} + \left. \frac{\partial \mathcal{L}}{\partial W} \right|_{W_0, \hat{x}_1} + \left. \frac{\partial^2 \mathcal{L}}{\partial W^2} \right|_{W_0, \hat{x}_1} \left( -\eta \left. \frac{\partial \mathcal{L}}{\partial W} \right|_{W_0, \hat{x}_0} \right) \right),

W0에서 측정한 x0과 x1의 업데이트에, W0에서 측정한 x1의 업데이트의 일차미분(W에 대한 influence)에 앞서 일어난 모든 업데이트를 합한 값을 곱하여 추가하는 방식이다. 즉, 앞에서 일어났던 모든 W에 가해진 변화는, 새로 관측한 데이터포인트 x1에 의해 W가 변화한 정도만큼 추가로 W의 업데이트에 반영된다.

일반적으로 t번째 업데이트에 대해

wt≈w0−η∑i=0t−1∂L∂w∣w0,x^i+∑i=1t−1f(i)(1)w_t \approx w_0 - \eta \sum_{i=0}^{t-1} \left. \frac{\partial \mathcal{L}}{\partial w} \right|_{w_0, \hat{x}_i} + \sum_{i=1}^{t-1} f(i)\tag{1}

이 때 f는 다음과 같이 재귀적으로 정의된다

f(i)=−η∂2L∂w2∣w0,x^i(−η∑j=0i−1∂L∂w∣w0,x^j+∑j=0i−1f(j))f(i) = -\eta \left. \frac{\partial^2 \mathcal{L}}{\partial w^2} \right|_{w_0, \hat{x}_i} \left( -\eta \sum_{j=0}^{i-1} \left. \frac{\partial \mathcal{L}}{\partial w} \right|_{w_0, \hat{x}_j} + \sum_{j=0}^{i-1} f(j) \right)

(1)에서 first sum은 GA unlearning으로 소거되는 대상, 따라서 second sum이 Unlearning error가 됨

Second sum을 전개하면 f(1)=η2ctf(1)=\eta^2c_t, f(2)=η3ct−1f(2)=\eta^3c_{t-1},…이므로 t-1번째 항까지의 합은

η2ct+η3ct−1+...+η2+t−1c1\eta^2c_t+\eta^3c_{t-1}+...+\eta^{2+t-1}c_1

이 때 η\eta는 learning rate로 일반적으로 1보다 작은 값을 가지므로, 항이 exponential한 스케일로 작아진다. 따라서 second sum을 그냥 f(1)=η2ctf(1)=\eta^2c_t로 근사할 수 있다. 곧 second sum을 다음으로 근사한다.

η2ct=∑i=1t−1η2∂2L∂w2∣w0,x^i−∑j=0i−1∂L∂w∣w0,x^j\eta^2 c_t = \sum_{i=1}^{t-1} \eta^2 \left. \frac{\partial^2 \mathcal{L}}{\partial w^2} \right|_{w_0, \hat{x}_i} - \sum_{j=0}^{i-1} \left. \frac{\partial \mathcal{L}}{\partial w} \right|_{w_0, \hat{x}_j}

∑j=0i−1∂L∂w∣w0,x^j\sum_{j=0}^{i-1} \left. \frac{\partial \mathcal{L}}{\partial w} \right|_{w_0, \hat{x}_j}를 기댓값인 i(wt−w0)t\frac{i (w_t - w_0)}{t}로 근사하고 l-2 norm으로 정규화하면 다음과 같다.

η2ct≈η2∥wt−w0∥2t∑i=1t−1∂2L∂2w∣w0,x^i⋅wt−w0∥wt−w0∥2⋅i\eta^2 c_t \approx \eta^2 \frac{\|w_t - w_0\|_2}{t} \sum_{i=1}^{t-1} \left. \frac{\partial^2 \mathcal{L}}{\partial^2 w} \right|_{w_0, \hat{x}_i} \cdot \frac{w_t - w_0}{\|w_t - w_0\|_2} \cdot i

또한 다음 관계가 성립하고

∥∂2L∂w2∣w0,x^iwt−w0∥wt−w0∥2∥2≤∥∂2L∂w2∣w0,x^i∥2\left\lVert \frac{\partial^2 \mathcal{L}}{\partial \mathbf{w}^2} \bigg\rvert_{\mathbf{w}_0, \hat{x}_i}\frac{\mathbf{w}_t - \mathbf{w}_0}{\left\lVert \mathbf{w}_t - \mathbf{w}_0 \right\rVert_2}\right\rVert_2 \leq \left\lVert \frac{\partial^2 \mathcal{L}}{\partial \mathbf{w}^2} \bigg\rvert_{\mathbf{w}_0, \hat{x}_i} \right\rVert_2

헤시안의 induced l2-norm(spectral norm)은 헤시안의 singular value 중 최대값이므로(by definition) 그 값을 σ\sigma라 두면 다음 부등식이 성립한다.

∥η2ct∥2≤η2∥wt−w0∥2t⋅σ⋅t(t−1)2\left\lVert \eta^2 c_t \right\rVert_2 \leq \eta^2 \frac{\left\lVert \mathbf{w}_t - \mathbf{w}_0 \right\rVert_2}{t} \cdot \sigma \cdot \frac{t(t - 1)}{2}

따라서 GA에서 고려되지 못하는 Second Sum을 Unlearning Error라 하며 위 식의 우변, 곧 다음과 같다.

e=η2⋅∥wt−w0∥2t⋅σavg⋅t2−t2e = \eta^2 \cdot \frac{\lVert \mathbf{w}_t - \mathbf{w}_0 \rVert_2}{t} \cdot \sigma_{\text{avg}} \cdot \frac{t^2 - t}{2}

본 논문에서는, model pruning을 통해 ∥wt−w0∥2\lVert \mathbf{w}_t - \mathbf{w}_0 \rVert_2을 작게 만들면 unlearning error, 즉 retrained model과 unlearned model의 차이를 줄일 수 있다고 주장한다.

논문의 Proposition은 다음과 같다.

0과 1로 구성되어 있고 모델과 같은 크기를 가지는 마스킹 벡터 m에 대해 unlearning error e(m)은

e(m)=O(η2t∥m⊙(θt−θ0)∥2σ(m))e(m) = \mathcal{O}(\eta^2 t \lVert m \odot (\theta_t - \theta_0) \rVert_2 \sigma(m))

위 proposition에 따라 GA에서 모델의 sparsity가 증가할수록 unlearning error가 감소한다. 저자는 GA 뿐 아니라 다른 approximate unlearning method에 대해서도 일반적으로 위 관계가 성립할 것이라 추측한다.

Sparsity-aided MU를 구현하기 위한 두 가지 방법을 제시한다.

1. Prune first, then unlearn

모델을 먼저 pruning하고 unlearning을 수행하는 방법이다.

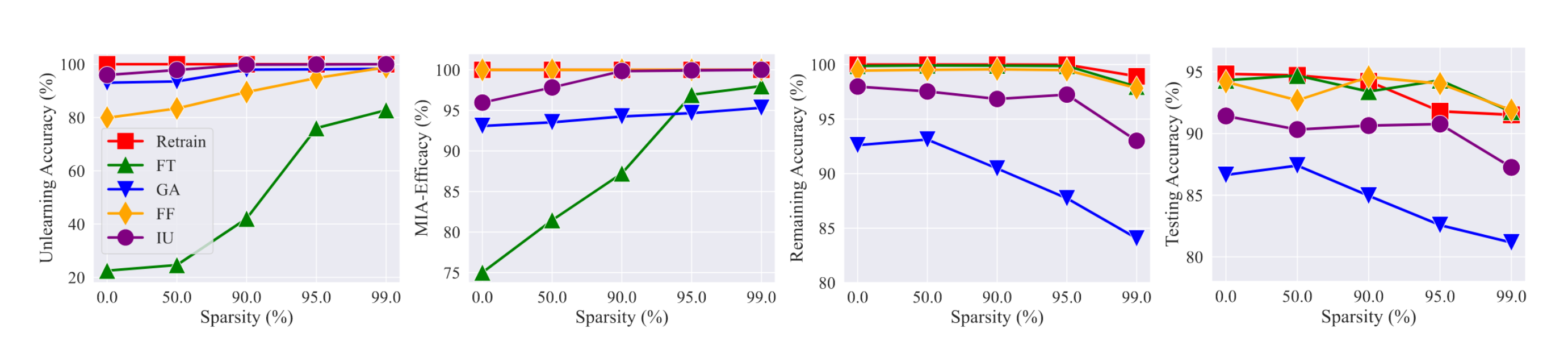
GA뿐 아니라 다양한 MU 방법에 대해서 sparse model의 unlearning 성능이 우수하다.

다음은 다양한 pruning method에 따른 unlearning 수행 결과이다.

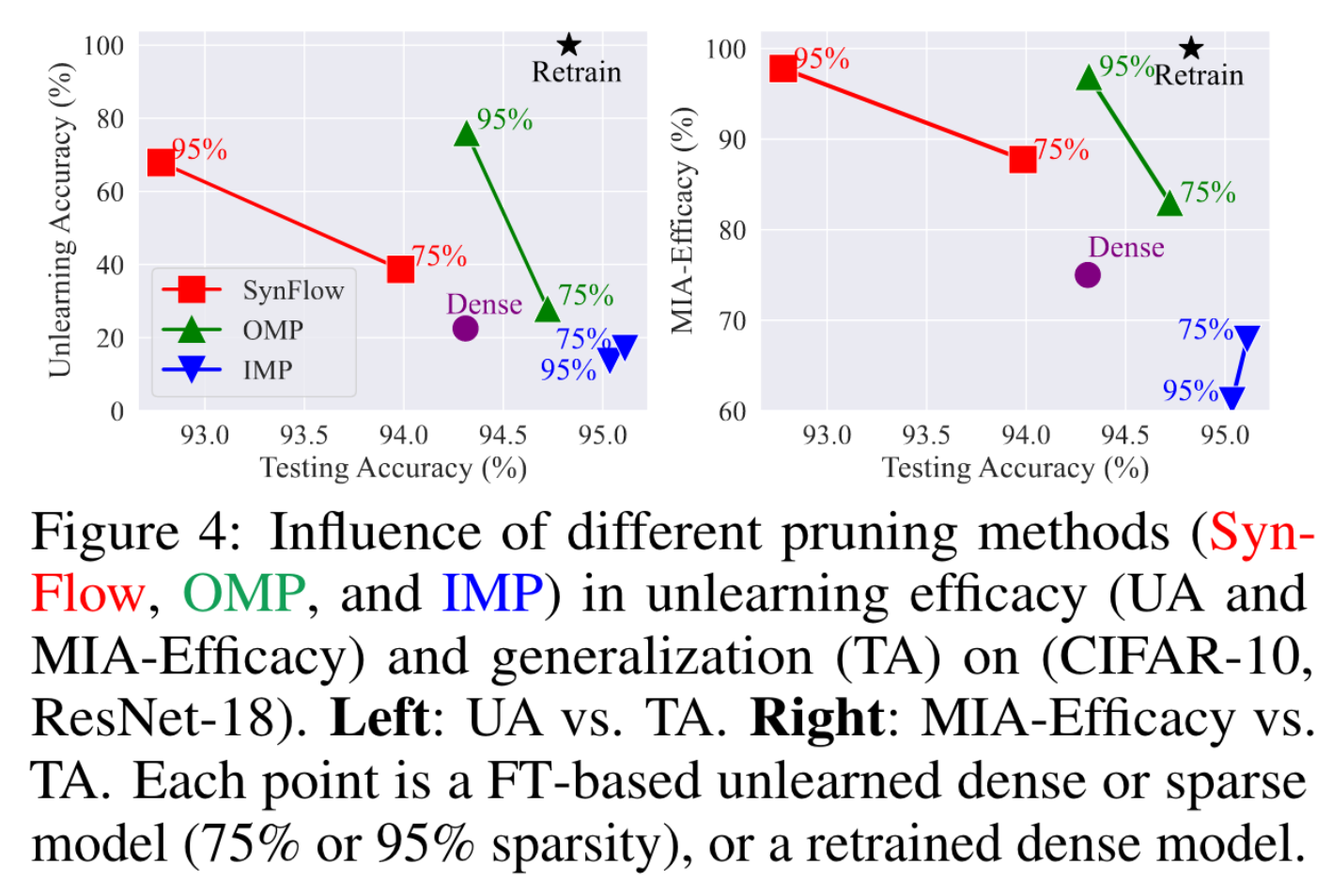
Retrain과 가까운 결과를 내는 OMP를 default pruning method로 사용함

2. Sparsity-aware unlearning

Unlearning objective에 sparsity에 대한 penalty항을 도입해 unlearning과 pruning을 함께 수행

θu=arg⁡min⁡θLu(θ;θo,Dr)+γ∥θ∥1,\theta_u = \arg \min_\theta L_u(\theta; \theta_o, D_r) + \gamma \|\theta\|_1,

이 때 LuL_u는 DrD_r에 대한 fine-tuning objective

감마에 따른 결과는 다음과 같다.

감마가 decaying되는 경우에 가장 좋은 성능

Experiments

  1. Prune first, then unlearn
  • ResNet18, CIFAR10
  • Classwise-forgetting은 10개 클래스에 대해 한 개씩 총 10회 수행한 결과의 평균과 표준편차
  • Random data forgetting ratio는 전체의 10%로 설정

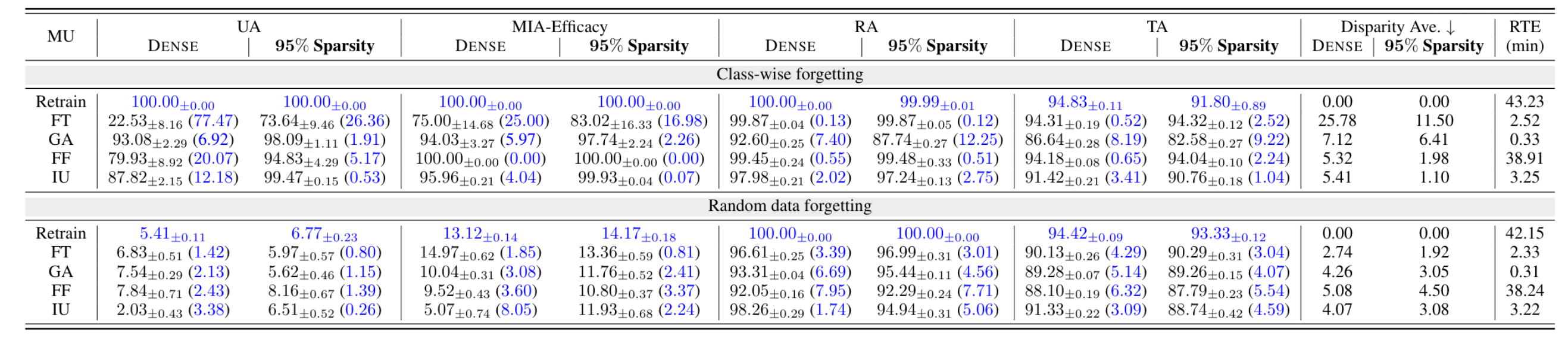
  • 전반적으로 모델이 sparse 해질수록 Retrained model과의 performance gap이 작아짐(Disparity Ave Dense vs 95% Sparsity)
  • FT가 RA와 TA에서 가장 높은 점수 달성, 그러나 낮은 UA와 MIA-Efficacy(Retain-Forget tradeoff)
  • GA가 가장 낮은 RA 달성(DrD_r을 사용하지 않기 때문)
  • FF는 Random data forgetting일때 Class-wise forgetting보다 비효과적(왜?)
  • IU에 95% model sparsity가 적용된 경우에 전반적으로 exact unlearning과 차이가 가장 작았다.(두 세팅에서의 disparity ave 평균)
  1. Sparsity-aware unlearning
  • ResNet18, CIFAR10

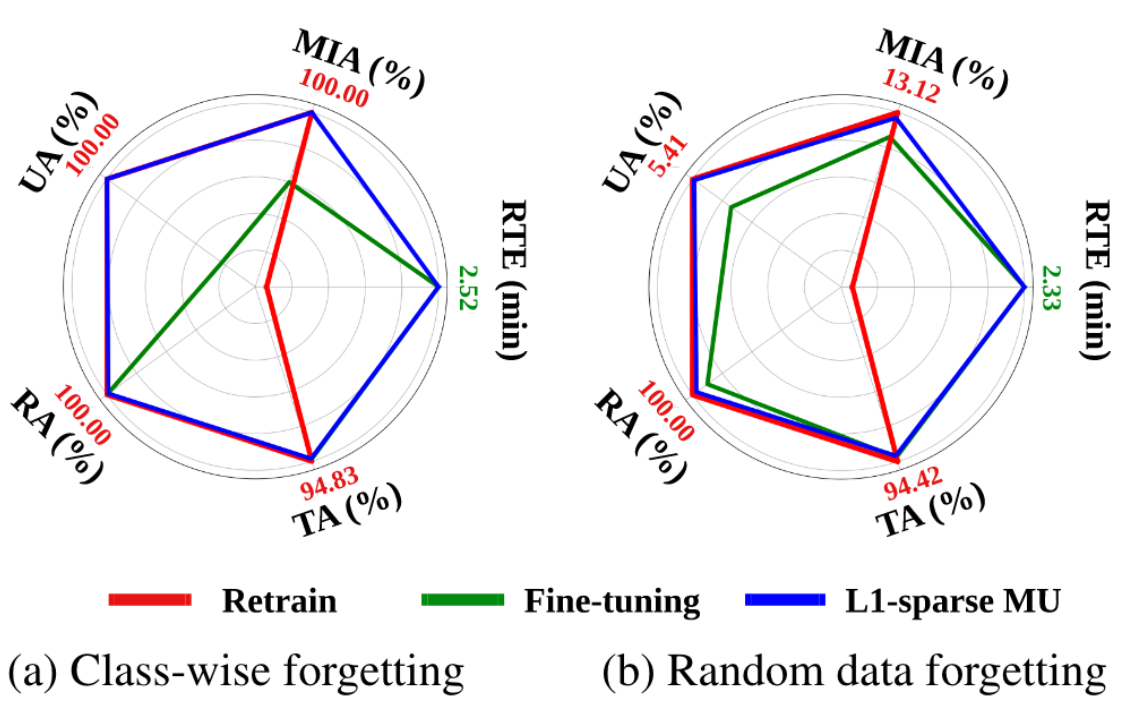
  • UA와 MIA-Efficacy에서 Sparse model이 outperform
profile
이휘영
이전 포스트

LLM Unlearning - Literature Review 1

다음 포스트

TOFU: A Task of Fictitious Unlearning for LLMs(Maini et al.,2024,arXiv)

0개의 댓글