(2) 그리디 & 구현

그리디 알고리즘(탐욕법)

그리디 알고리즘은 현재 상황에서 지금 당장 좋은 것만을 고르는 방법을 의미함, 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구함

정당성 분석이 중요함. 단순히 가장 좋아보이는 것만을 선택해도 최적의 해를 구할 수 있는지 검토하는 과정이 필요함

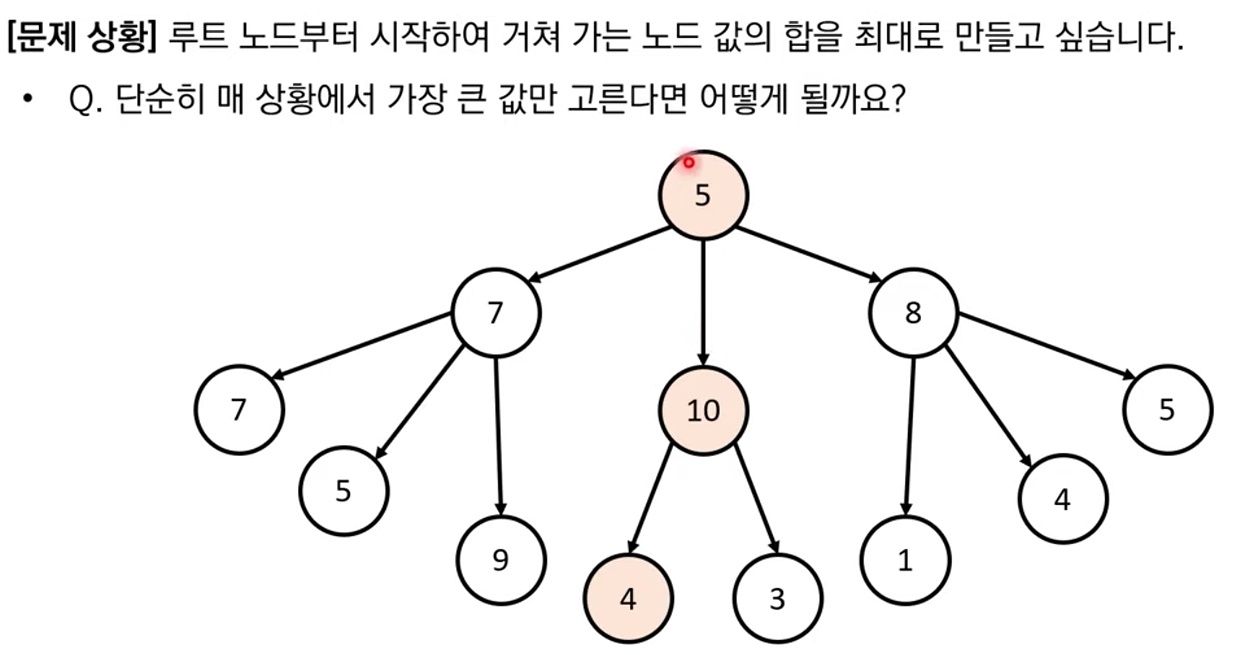
위의 그래프에서 최적의 경로를 찾는다면, 5➡️7➡️9 (합:21)이 될 것이다. 하지만 그리디 알고리즘의 경우 당장 좋은 것만을 고르므로 5➡️10➡️4 (합:19)의 결과를 도출한다.

따라서, 그리디 알고리즘은 최적의 해를 보장할 수 없을 경우가 많음. 하지만 코딩테스트의 대부분에서 그리디 문제는 탐욕법으로 얻은 해가 최적의 해가 되는 상황을 추론가능해야 풀리도록 설계돼있음

• 거스름돈 문제를 예제로 들 수 있음.

  • 가장 단위가 큰 화폐부터 거슬러 줄 경우 최적의 해를 보장함. 가지고 있는 동전 중 가장 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전의 조합으로 최적의 해가 나올 수 없기 때문!
    ➡️ 그리디 알고리즘의 경우 정당성 검토가 중요

• 곱하기 혹은 더하기 문제.

  • 0부터 9로 이루어진 문자열을 왼쪽에서부터 순서대로 "+"와 "x"만 사용하여 계산할 때, 나올 수 있는 가장 큰 수를 구하시오.
  • 이 문제는 순차적으로 계산할 때, 주어진 숫자가 "0"와 "1"이면 더하고, 그 외의 숫자일 경우는 더한다고 계산해 최적의 해를 구할 수 있음.

  data = input()
  result = int(data[0])
  
  for i in range(1, len(data)
  num = int(data[i])
  if num <= 1 or result <= 1:
  result += num
  else:
  result *= num
  
  print(num)

구현

시뮬레이션과 완전탐색에 초점

구현이란, 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정

구현 유형의 문제는 풀이를 떠올리는 것은 쉽지만 소스코드로 옮기기 어려움

구현 유형의 예시

• 알고리즘은 간단한데 소스가 지나칠만큼 길어지는 문제
• 실수 연산을 다루고, 특정 소수점 자리까지 출력해야하는 문제
• 문자열을 특정한 기준에 따라 끊어 처리해야하는 문제
• 적절한 라이브러리를 찾아서 사용해야하는 문제

일반적으로 알고리즘 문제에서의 2차원 공간은 행렬의 의미로 사용됨
왼쪽 위의 위치가 (0,0) 또는 방향 벡터가 주어짐.

• 상하좌우 문제를 예시로 들 수 있음.

  • N X N 크기의 정사각형 공간에 서있고, 가장 왼쪽 위는 (1,1)이며 가장 오른쪽 아래는 (N,N). 공간을 넘어가는 구현은 무시. 마지막 위치를 반환.

  n = int(input())
  x,y = 1,1
  plans = input().split()
  
  dx = [0,0,-1,1]
  dy = [-1,1,0,0]
  move_types = ['L', R','U','D']
  
  for plan in plans:
  	for i in range(len(move_types))
    	if plan == move_types[i]:
    		nx = x - dx[i]
        	ny = y - dy[i]
    if nx < 1 or ny < 1 or nx > n or ny > n:
    	continue
    x, y = nx, ny 
  print(x,y)