코딩테스트를 대비한 알고리즘 포스팅 해시(Hash)편은 여기 참고 !
코딩테스트를 대비한 알고리즘 포스팅 스택/큐(Stack/Queue)편은 여기 참고 !
코딩테스트를 대비한 알고리즘 포스팅 힙(Heap)편은 여기 참고 !
🐇 정렬이란 ?
네번째로 정리할 알고리즘인 정렬(Sort)은 어떤 데이터셋이 주어졌을 때, 이를 정해진 순서대로 나열하여 재배치하는 문제이다. 즉, 섞여있는 데이터를 순서대로 나열하는 것. 정렬 알고리즘은 시간복잡도에 따라 성능이 좌우되며 성능이 높을수록 구현이 어렵다.
대표적인 정렬 알고리즘에는
버블정렬, 선택정렬, 삽입정렬, 병합정렬, 퀵정렬이 있다.
버블정렬, 선택정렬, 삽입정렬은 O(n2)의 시간복잡도를,
병합정렬, 퀵정렬은 O(nlogn)의 시간복잡도를 갖는다.
버블정렬(Bubble sort)
버블정렬은 인접한 두 수를 비교하며 정렬해나가는 방법으로, O(n2)의 느린 성능을 가지고 있다. 앞에서부터 시작해 큰 수를 점차 뒤로 보내며 뒤가 가장 큰 값을 가지도록 하는 방법과 뒤에서부터 시작해 작은 수를 점차 앞으로 보내며 앞에서부터 정렬을 완성하는 방법이 있다.
이는 거의 모든 상황에서 최악의 성능을 보여주지만, 이미 정렬된 자료에서는 1번만 순회하므로 최선의 성능을 보여주는 알고리즘이다. 데이터 하나가 순회할때마다 데이터 하나가 정렬되므로 거품이 올라오는 것처럼 보여서 버블정렬이라 한다. 원리가 직관적이라 구현은 쉽지만 비효율적이라 실무에선 거의 사용하지 않는다.
0번 인덱스 갑과 1번 인덱스 값을 비교 후 정렬
1번 인덱스 값과 2번 인덱스 값을 비교 후 정렬
...
n-1번 인덱스 값과 n번 인덱스 값을 비교 후 정렬파이썬으로 구현한 버블정렬
# array = [8,4,6,2,9,1,3,7,5]
array = [9,8,7,6,5,4,3,2,1]
def bubble_sort(array):
n = len(array)
for i in range(n - 1):
for j in range(n - i - 1):
if array[j] > array[j + 1]:
array[j], array[j + 1] = array[j + 1], array[j]
print(array)
print("before: ",array)
bubble_sort(array)
print("after:", array)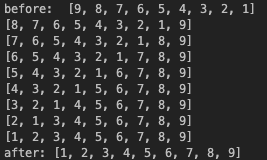
선택정렬(Selection sort)
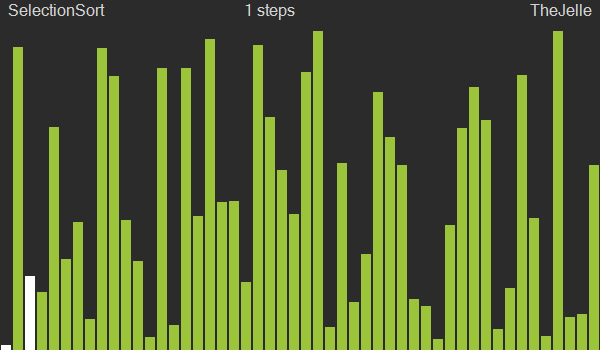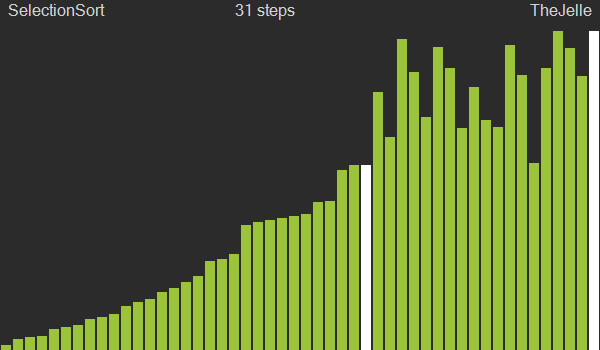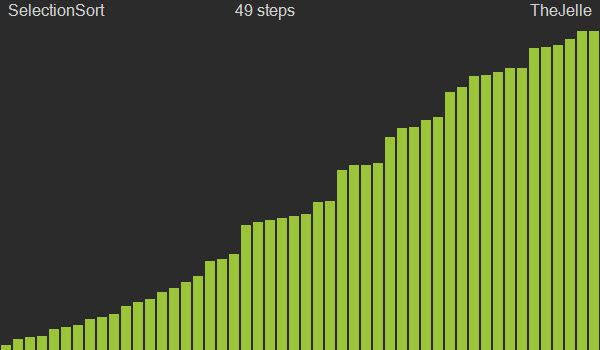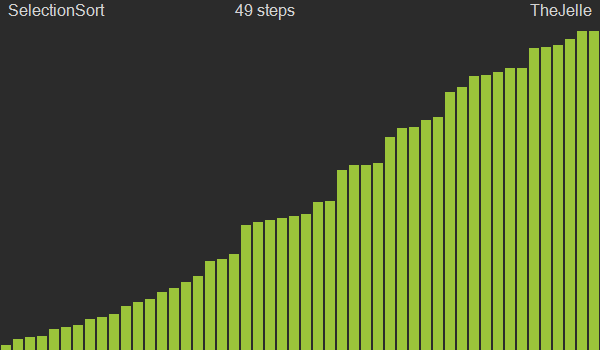
선택정렬은 한바퀴 돌때마다 가장 작은 값을 찾아 해당 인덱스 값과 위치를 교환하는 방법으로, 앞에서부터 정렬해나가는 특성을 가지고 버블정렬과 마찬가지로 O(n2)의 느린 성능을 가지고 있다.
한 번 순회를 돌게 되면 전체 자료 중 가장 작은 값의 자료가 0번째에 위치하게 되므로 그 다음 순회부터는 1번 인덱스부터 순회를 돌며 반복하게 된다. 선택정렬은 현재 자료의 정렬 여부에 관계없이 무조건 전체 리스트를 순회해가며 검사하므로 최선과 최악 모두 O(n2)의 시간복잡도를 갖는다.
0번 - n번 인덱스 값 중 가장 작은 값을 찾아 0번째 인덱스 값과 swap
1번 - n번 인덱스 값 중 가장 작은 값을 찾아 1번째 인덱스 값과 swap
...
n-1번 - n번 인덱스 값 중 가장 작은 값을 찾아 n-1번째 인덱스 값과 swap파이썬으로 구현한 선택정렬
array = [8,4,6,2,9,1,3,7,5]
def selection_sort(array):
n = len(array)
for i in range(n):
min_index = i
for j in range(i + 1, n):
if array[j] < array[min_index]:
min_index = j
array[i], array[min_index] = array[min_index], array[i]
print(array[:i+1])
print("before: ",array)
selection_sort(array)
print("after:", array)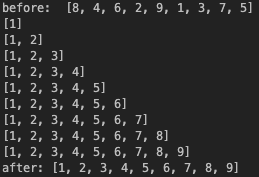
삽입정렬(Insertion sort)
삽입정렬은 정렬된 데이터 그룹을 늘려가며 추가되는 데이터를 알맞은 자리에 삽입하는 방법으로, 버블정렬 선택정렬과 마찬가지로 O(n2)의 느린 성능을 가지고 있다.
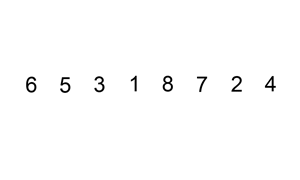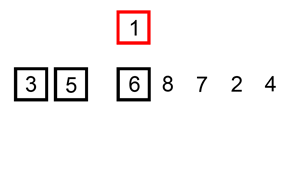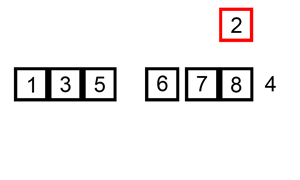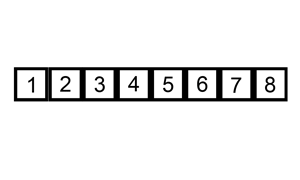
위의 영상보다 더 이해하기 쉬운 영상이 있어 가져와보았다.
주어진 자료(나중에 추가된 자료)를 앞에서부터 정렬된 자료 그룹과 비교하며 위치를 찾아 삽입하는 정렬로, 인간이 직접 정렬하는 순서와 가장 흡사하다. 최선의 경우 전체 자료를 한번만 순회하면 되기 때문에 O(n)의 시간복잡도를 가지지만, 최악의 경우 O(n2)의 시간복잡도를 갖는다.
0번 인덱스를 건너뛴다.
0 - 1번 인덱스 중 1번 인덱스 값이 들어가야할 위치를 찾아서 넣는다.
0 - 2번 인덱스 중 2번 인덱스 값이 들어가야할 위치를 찾아서 넣는다.
...
0 - n번 인덱스 중 n번 인덱스 값이 들어가야할 위치를 찾아서 넣는다.파이썬으로 구현한 삽입정렬
array = [8,4,6,2,9,1,3,7,5]
def insertion_sort(array):
n = len(array)
for i in range(1, n):
for j in range(i, 0, - 1):
if array[j - 1] > array[j]:
array[j - 1], array[j] = array[j], array[j - 1]
print(array[:i+1])
print("before: ",array)
insertion_sort(array)
print("after:", array)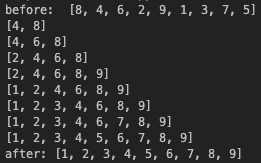
병합정렬(Merge sort)
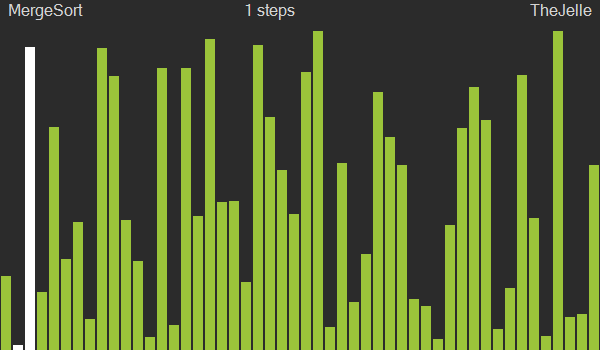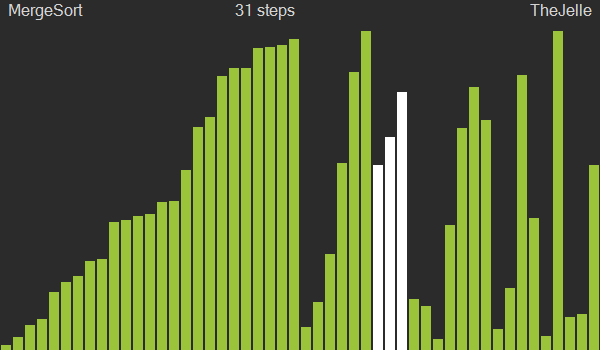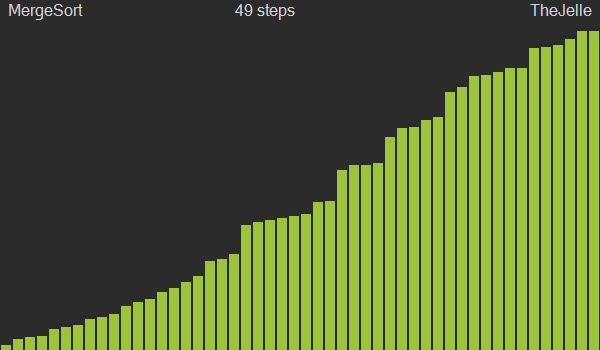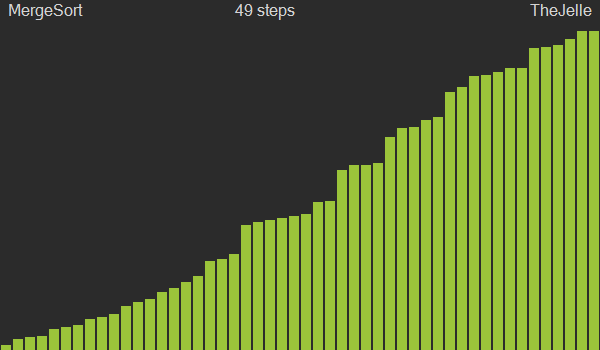
병합정렬은 분할정복과 재귀를 이용한 알고리즘으로, 큰 문제를 작은 여러 개의 문제로 쪼개서 각각을 해결한 후 결과를 모아서 원래의 문제를 해결하는 방법이다. 문제를 반으로 쪼개고 다시 합치는 과정에서 그룹을 만들어 정렬하게 되며, 이 과정에서 2n개의 공간이 필요하지만, O(nlogn)의 시간복잡도를 가져 앞선 세 정렬보다 괜찮은 성능을 보인다.
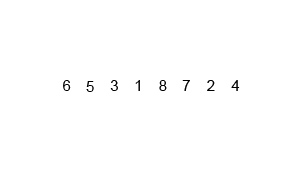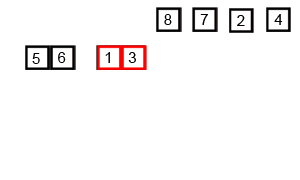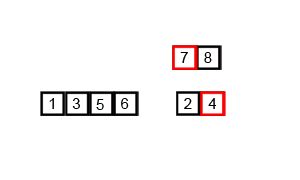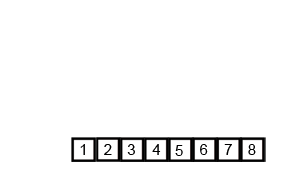
[6, 5, 3, 1, 8, 7, 2, 4]
[6, 5] [3, 1] [8, 7] [2, 4]
2개씩 분할해 그룹끼리 비교 후 정렬
[5, 6] [1, 3] [7, 8] [2, 4]
[5, 6] [1, 3]
(1과 5 비교) -> [1] (5와 3 비교) -> [1, 3] (5와 6 비교) -> [1, 3, 5, 6]
[7, 8] [2, 4]
(7과 2 비교) -> [2] (7과 4 비교) -> [2, 4] (7과 8 비교) -> [2, 4, 7, 8]
[1, 3, 5, 6] [2, 4, 7, 8]
(1과 2 비교) -> [1] (3과 2 비교) -> [1 , 2]
(3과 4 비교) -> [1, 2, 3] (5와 4 비교) -> [1, 2, 3, 4]
(5와 7 비교) -> [1, 2, 3, 4, 5] (6과 7 비교) -> [1, 2, 3, 4, 5, 6]
(7과 8 비교) -> [1, 2, 3, 4, 5, 6, 7, 8]파이썬으로 구현한 병합정렬
array = [8,4,6,2,9,1,3,7,5]
def merge_sort(array):
if len(array) < 2:
return array
mid = len(array) // 2
low_arr = merge_sort(array[:mid])
high_arr = merge_sort(array[mid:])
merged_arr = []
l = h = 0
while l < len(low_arr) and h < len(high_arr):
if low_arr[l] < high_arr[h]:
merged_arr.append(low_arr[l])
l += 1
else:
merged_arr.append(high_arr[h])
h += 1
merged_arr += low_arr[l:]
merged_arr += high_arr[h:]
print(merged_arr)
return merged_arr
print("before: ",array)
array = merge_sort(array)
print("after:", array)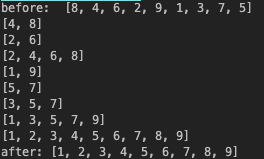
퀵정렬(Quick sort)
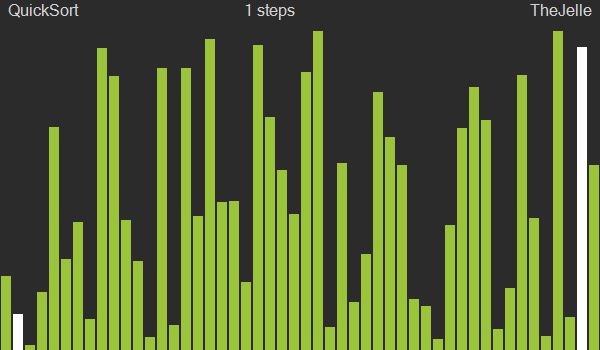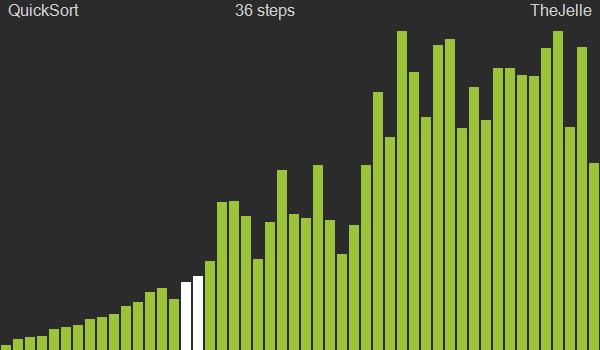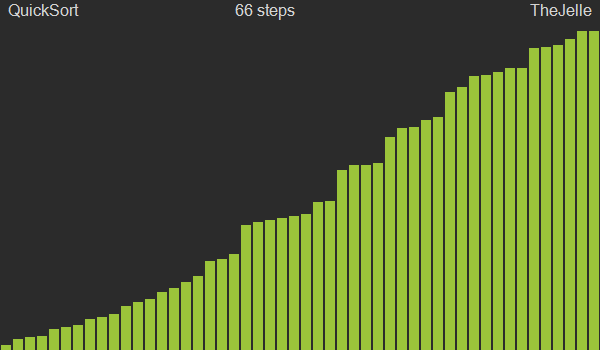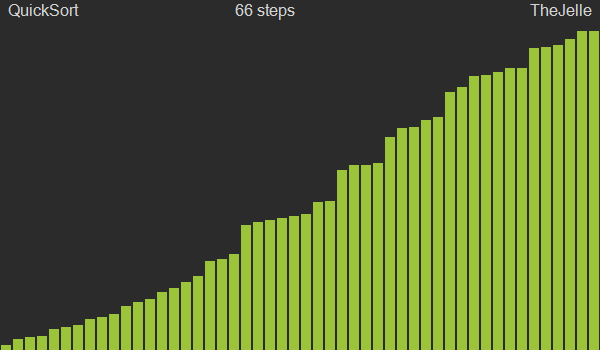
퀵정렬도 병합정렬과 마찬가지로 분할정복을 통한 정렬 방법으로, 동일하게 O(nlogn)의 시간복잡도를 갖는다. 다만 병합정렬은 분할 단계에서는 아무것도 하지 않고 병합하는 단계에서 정렬을 수행하지만 퀵정렬은 분할 단계에서 중요한 작업들을 수행하고 병합시에는 아무것도 하지 않는다는 것이 차이점이다.
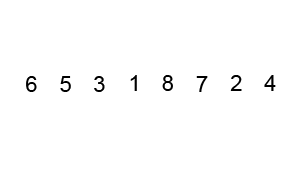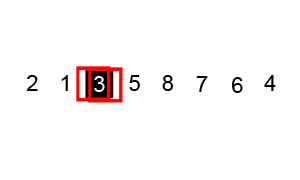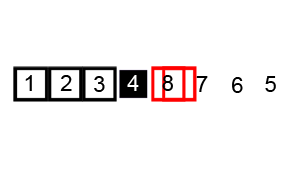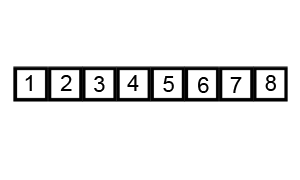
또한 병합정렬은 균등하게 분할하였다면 퀵정렬은 pivot을 설정하고 그 기준으로 정렬을 수행한다.
입력된 자료 리스트에서 하나의 데이터를 고르고 이 데이터를 `pivot`이라 한다.
`pivot`을 기준으로 리스트를 둘로 분할한다.
`pivot`을 기준으로 해당 데이터보다 작은 데이터는 모두 `pivot`의 왼쪽으로 옮긴다.
`pivot`을 기준으로 해당 데이터보다 큰 데이터는 모두 `pivot`의 오른쪽으로 옮긴다.파이썬으로 구현하는 퀵정렬
array = [8,4,6,2,5,1,3,7,9]
def quick_sort(array):
if len(array) <= 1:
return array
pivot = len(array) // 2
front_arr, pivot_arr, back_arr = [], [], []
for value in array:
if value < array[pivot]:
front_arr.append(value)
elif value > array[pivot]:
back_arr.append(value)
else:
pivot_arr.append(value)
print(front_arr, pivot_arr, back_arr)
return quick_sort(front_arr) + quick_sort(pivot_arr) + quick_sort(back_arr)
print("before: ",array)
array = quick_sort(array)
print("after:", array)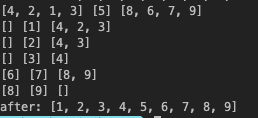
✏️ python에서 정렬을 구현하는 방식: sort(), sorted()
python에서 자료를 정렬할 때는 리스트에 sort() 메서드를 적용하는 방법과 sorted() 내장함수를 사용하는 방법이 있다.
list.sort()
sorted(list)sort()
python 3.10.5 manual
This method modifies the sequence in place for economy of space when sorting a large sequence. To remind users that it operates by side effect, it does not return the sorted sequence (use sorted() to explicitly request a new sorted list instance).
sort함수는 리스트명.sort() 형식으로 이용하는 리스트형(전용) 함수이다. 즉, 이 함수는 입력값으로 리스트밖에 받지 못함 !
이 함수는 리스트 원본 값을 직접 수정한다. 따라서 정렬을 수행한 리스트를 따로 반환하지는 않는다.
sorted()
python 3.10.5 manual
Return a new sorted list from the items in iterable. ... The built-in sorted() function is guaranteed to be stable. A sort is stable if it guarantees not to change the relative order of elements that compare equal — this is helpful for sorting in multiple passes (for example, sort by department, then by salary grade).
sorted함수는 sorted(리스트명) 형식으로 이용하는 파이썬 내장함수이다. sort함수는 리스트 형식만 인자로 받을 수 있는 반면, sorted()함수는 어떤 형식이든 받을 수 있다.
이 함수는 리스트 원본 값은 수정하지 않고 원본 값은 유지하는 대신 정렬 작업을 수행한 후의 값을 반환한다.
둘을 어떤 상황에 사용하면 좋을까?
- 원본을 유지해야 할 때에는
sorted()함수 - 리스트 외에 다른 자료형을 정렬할 때에는
sorted()함수 - 원본 유지가 필요 없을 때에는 시간, 공간 절약을 위해
sort()함수 list만 이용할 때에는 시간, 공간 절약을 위해sort()함수
파이썬 sorted 내장함수의 내부 알고리즘
python 3.10.5 manual
The Tim sort algorithm used in Python does multiple sorts efficiently because it can take advantage of any ordering already present in a dataset.
파이썬의 sorted() 함수는 Tim sort 알고리즘을 이용한다.
Tim sort란 2002년 소프트웨어 엔지니어 Tim Peters에 의하여 만들어진 알고리즘으로, 앞에서 언급했던 Insert sort와 Merge sort를 결합하여 만든 Hybrid stable sorting 알고리즘이다.
이 알고리즘은 미리 어느 정도 정렬된 부분이 존재하는 실생활 데이터의 특성을 고려하여 더 빠르게 작동하도록 고안된 알고리즘으로, 최선의 시간복잡도는 O(n), 평균은 O(nlogn), 최악은 O(nlogn)의 시간복잡도를 가진다.
이 알고리즘은 python 외에도 java, android, google chrome, 그리고 swift까지 많은 프로그래밍 언어에서 표준 정렬 알고리즘으로 채택되어 사용되고 있다 !
Tim sort 알고리즘에 대해 더 자세한 내용을 알고 싶다면 이 블로그를 참고하자 !
해당 포스팅을 작성하는데 참고한 블로그
정렬 알고리즘을 활용한 코딩테스트 문제 풀이