Divide & Conquer
-
Recursion 기반
-
문제해결 시나리오
- 분할 : 주어진 문제를 두 개 혹은 그 이상의 같은 형식으로 나눔
- 정복 : 나누어진 문제를 재귀적으로 해결 나누어진 문제를 더 이상 나누어 문제를 필요없을때까지 계속 분할, 해결
- 통합 : 나누어서 해결한 문제들을 통합해서 원래 문제의 해답을 만듬
-
분할 정복은 Top-Down의 방법
- 초기의 큰 문제를 직접 해결할 수 없기 떄문에 적절한 크기로 분할하여 해결하는 방법
- binary search, n개의 구슬 중 가벼운 구슬 찾기
-
Recursion
- Top-down으로 분할된 문제를 해결할 수 없을 경우 직접 해결할 수 있을떄까지 재귀적으로 분할
-
수학적 귀납법으로 알고리즘의 정확성 증명, 재귀식(점화식)으로 시간 복잡도 계산
수학적 귀납
- 정수 n에 대한 P(n)
- k>=a를 만족하는 모든 k에 대하여 p(k)가 참이라고 가정
- 2번의 가정을 통해 p(k+1)이 참임을 증명하면 결론적으로 a보다 큰 모든 k에대한 p(n)이 참


- 중간에 가정한 p(k)를 활용함
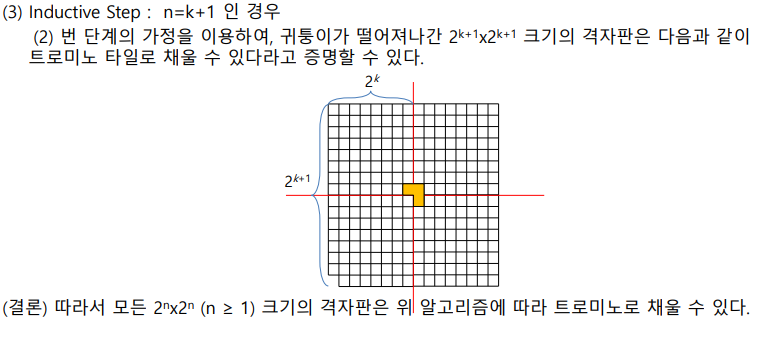
트로미노 채우기

- 귀퉁이가 하나 떨어져있어야 가능
- 이걸 분할정복으로 귀퉁이가 떨어진 여러개의 작은 타일로 나누는게 관점
- 가운데에 트로미노를 하나 놓고 4개로 나누면 귀퉁이가 없는 4개의 타일이 만들어짐
- 트로미노 하나로 타일을 다 채울수 있을떄까지(타일이 2x2크기) 재귀적으로 분할
- 증명
- 귀퉁이 말고 다른 위치가 없으면?
- 트로미노를 다른 위치로 놓으면 가능
Finding Max
- 최대값 찾기
- 배열을 계속 반으로 나누어서 왼쪽 오른쪽중 최대값을 리턴
- 배열의 크기가 1일떄까지 나누고 1이면 그 값을 그냥 리턴

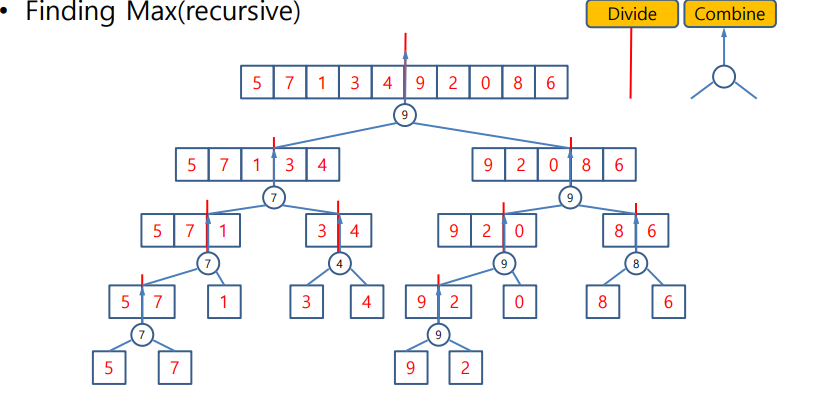
- O(n)
Binary Search
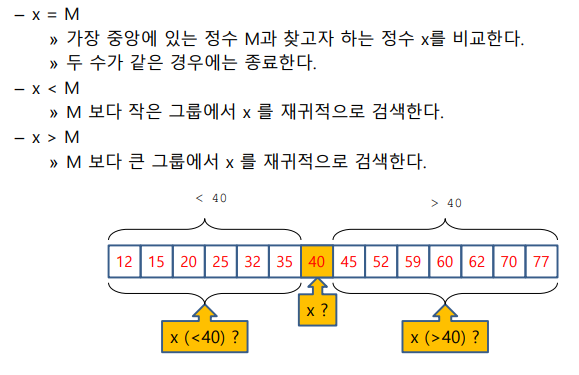
- 오름차순으로 정렬된 n개의 정수가 저장된 배열에서 정수 x가 들어있는지 검사
- Divide
- 중앙에 있는 정수 m과 m보다 작은 왼쪽 그룹, m보다 큰 오른쪽 그룹으로 나움
- conquer
- combine
- 분할된 구간에서 구한 해답을 원래 문제의 해답으로 정한다
- Analysis
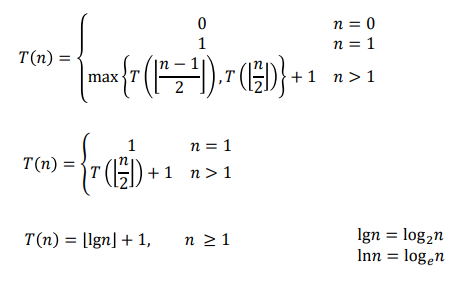
- lgn = log2n
- R(n) = 정수 n을 연속적으로 2로 나누어서 1이 될떄까지 나누는 횟수


- n이 2^k일떄
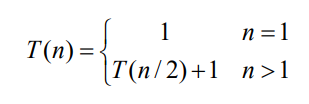
find peak value
- 정렬이 되어있지 않고 오르다 내려가는 산모양 형태의 수열이 있을때 이 수열의 최고점을 계산하는 방법

- 가운데로 계속 나누면서 왼,오가 둘다 작으면 피크 왼쪽이 작고 오른쪽이 크면 피크가 오른쪽에 있음, 왼쪽이 크고 오른쪽이 작으면 피크가 왼쪽에 있음
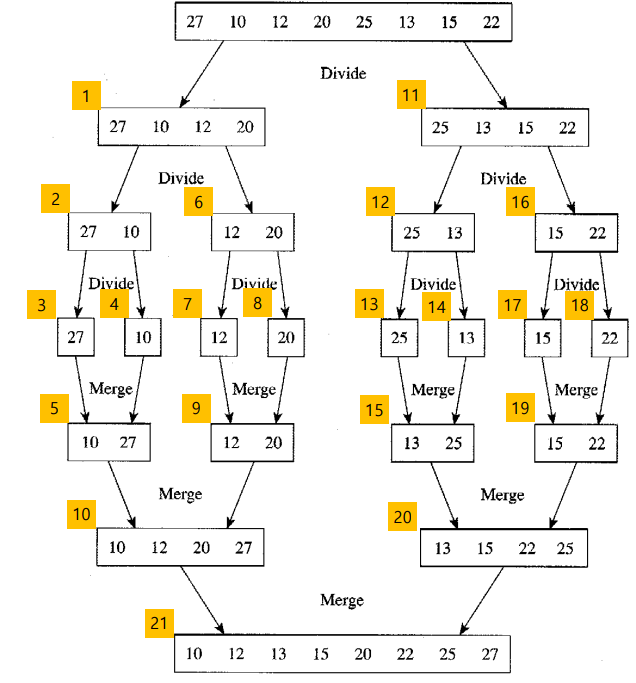
Merge Sort
- Divide
- 배열을 n/2개의 데이터로 분할
- Conquer
- 나누어진 배열을 재귀적으로 합병 정렬
- 데이터의 개수가 1일때는 정렬된 상태
- combine
- 두 개의 이미 정렬된 부분배열을 통합하여 n개의 정렬된 배열로 만듬
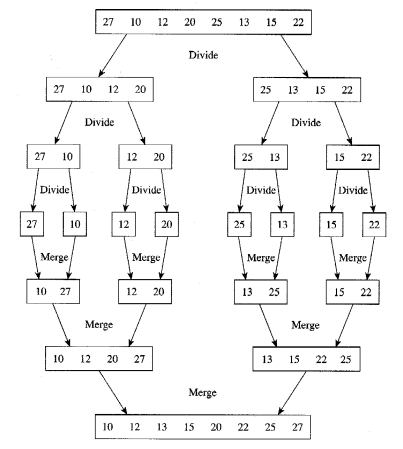
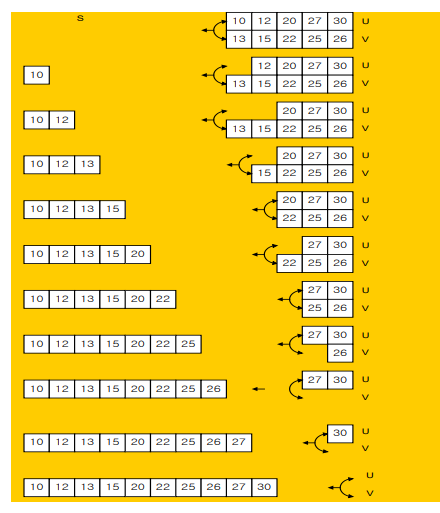
- combine(merge) 과정
- 양쪽의 배열 첫번째부터 비교 시작
- 더 작은쪽을 합친 배열의 처음에 위치
- 위치시킨 배열은 두번쨰, 반대쪽은 첫번쨰를 비교
- 그 중 더 작은쪽을 합친 배열 두번쨰에 위치
- 위치시킨 배열의 인덱스 1증가
- not in-place임
- merge과정에서 merge한 후의 결과를 저장할 새로운 배열이 필요하기 때문에
- stable
- 위의 비교과정에서 값이 같으면 left를 먼저 옮기는 방식으로 하기 때문에
- 실행순서
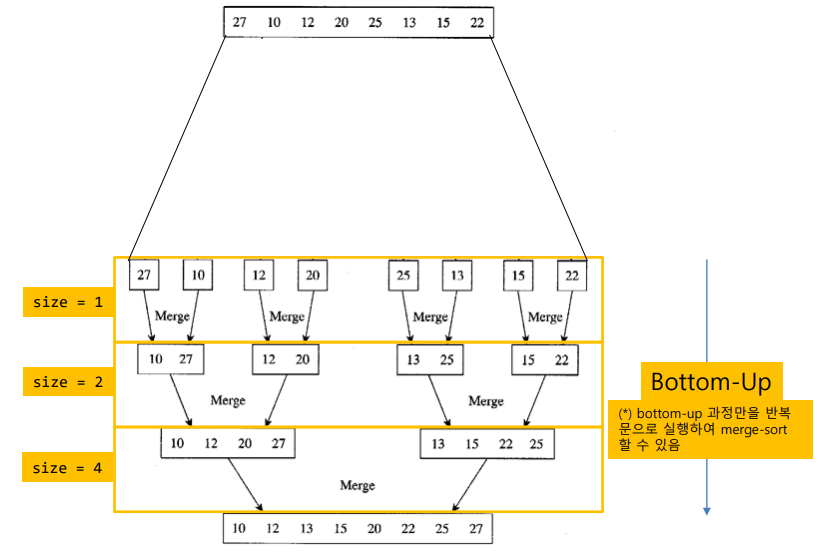
- 반복문으로 mergesort
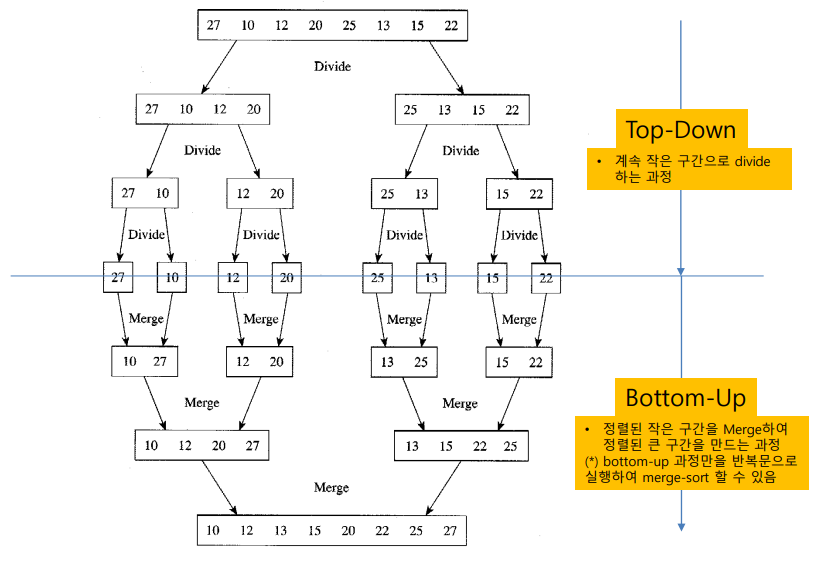
- 데이터가 작은부분에서 많은 과정으로 가능 Bottom-Up과정만을 가지고 반복문으로 구현 가능
- divide과정이 원본 배열의 순서 그대로 한칸씪 나누기만 하기 때문
- Analysis
- 왼쪽, 오른쪽의 분할 + merge


MCSS
- Kadane도 있지만 divide conquer도 가능
- 반으로 나눈 배열에서 왼쪽, 오른쪽의 부분에서 최대 구간이나 중간을 지나가는 최대 구간중 최대 구간이 전체의 답이 된다
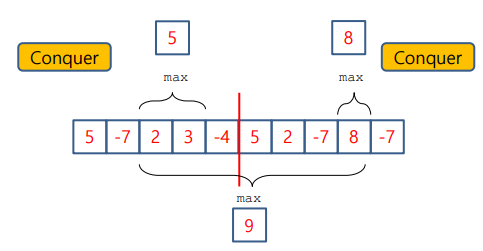
- Analysis
- 배열의 숫자를 더하는 연산
- mergesort와 동일
- O(nlogn)
Quick sort
- 배열중 임의의 데이터를 pivot으로 설정
- pivot을 기준으로 왼쪽, 오른쪽으로 나누고 각각에서 pivot을 설정해 recursive하게 정렬
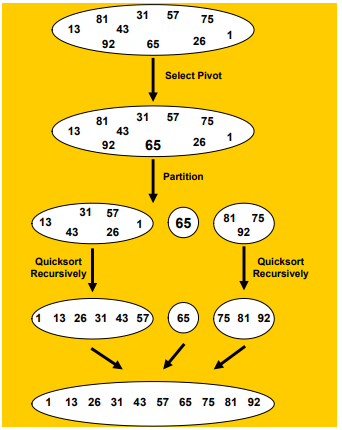
- pivot의 선택 방법
- median of three
- 가장 왼쪽, 오른쪽 중간 데이터 중 값이 중간인 데이터를 가장 왼쪽에 위치하게 함(swap으로 pivot이 가장 왼쪽으로 이동하게)

- median of three
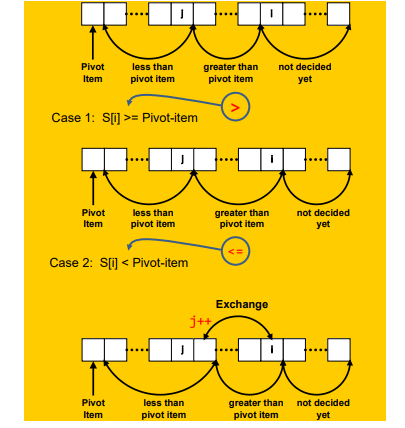
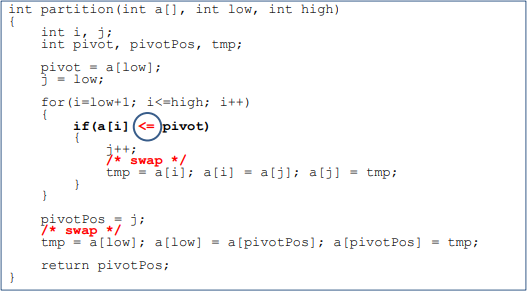
- Divide by Romuto
- pivot을 제일 왼쪽에 두고 반복문으로 pivot다음부터 시작해 두개의 인덱스로 pivot보다 작은 원소를 왼쪽 큰 원소를 오른쪽에 위치하게
- j는 pivot보다 작은 원소가 i에 걸렸을때 j위치에 i원소를 위치시키고 j를 1증가 시킴
- j가 반복문이 끝났을떄 pivot의 크기를 기준으로 왼,오로 나누어줌
- 마지막에 pivot과 j의 위치를 바꾸면 pivot은 제위치로 찾아간것(combine 과정이 필요 없음)
- 이후 제귀적으로 퀵 정렬 실행
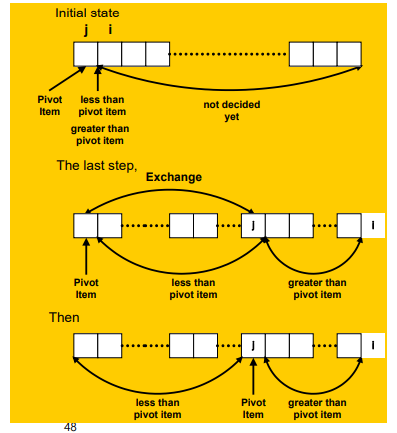
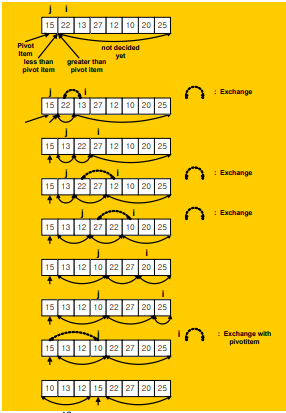
- pivot을 제일 왼쪽에 두고 반복문으로 pivot다음부터 시작해 두개의 인덱스로 pivot보다 작은 원소를 왼쪽 큰 원소를 오른쪽에 위치하게
- Analysis
- n개의 데이터에서 pivot과 비교하는 연산의 횟수 = n-1
- base case가 필요없음 : 비교할 원소가 1개일때 아무것도 안함

- not stable, not in-place
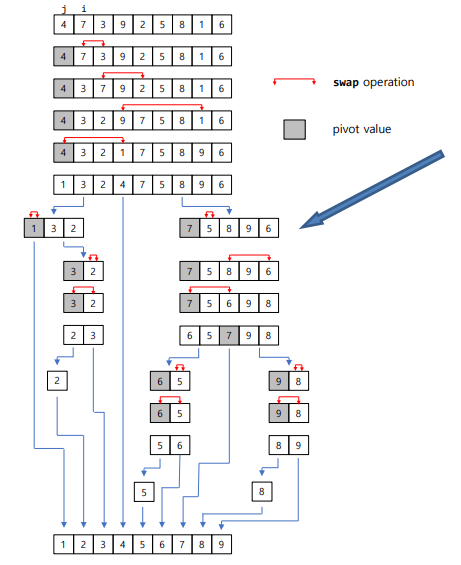
이거 중요함
- 퀵소트의 worst case는 미리 정렬된 데이터가 입력되는 경우

- O(n^2) 미리 정렬된 데이터에서 그냥 제일 왼쪽 원소를 pivot으로 사용하면 느리기 떄문에 median of 3를 활용해 pivot을 먼저 바꿔준 후 사용함
- pivot으로 매번 배열이 반반씩 나누어지면(best case) O(nlogn)으로 줄어듬
- best, worst둘다 퀵 정렬에서는 드물기 때문에 average case를 사용함
- 배열에 속하는 데이터가 모두 같은 확률로 pivot이 된다고 가정
- 모든 i가 pivot을 경우의 time complexity를 더하고 n으로 나눔

- O(nlogn)
- in-place가 아닌 이유
- 재귀적으로 구현되어있음
- 이때 call-stack에 activation record가 쌓이고 worst일때 O(logn)만큼 쌓임
- 만약 pivot으로 나눈 배열중 더 긴 부분부터 실행하게 되면 O(n)만큼이 필요함
- 짧은 배열부터 실행해야 O(logn) 필요
Quick Sort Partition by Hoare
- i와 j를 사용 i는 처음부터 j는 맨 끝부터 시작
- i가 피벗보다 작으면 계속 전진
- j는 피벗보다 크면 앞으로 전진
- 크면 뒤에 작으면 앞에 있게 만드는 과정이고 i가 피벗에서 시작하기 때문에 이 알고리즘에서는 피벗이 처음부터 위치가 바뀜
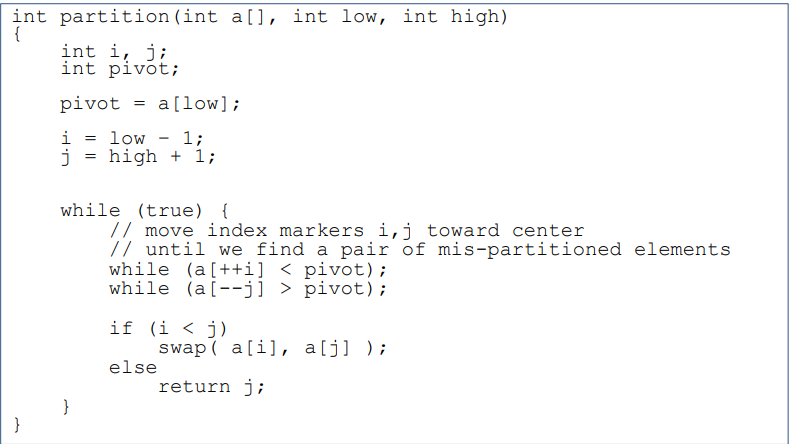
- i와 j의 위치가 역전되지 않았으면 두 값을 교환
- 그렇지 않으면 j를 리턴
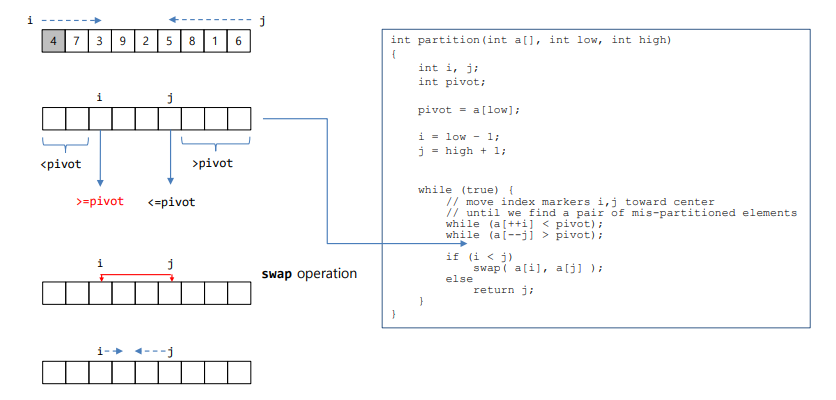
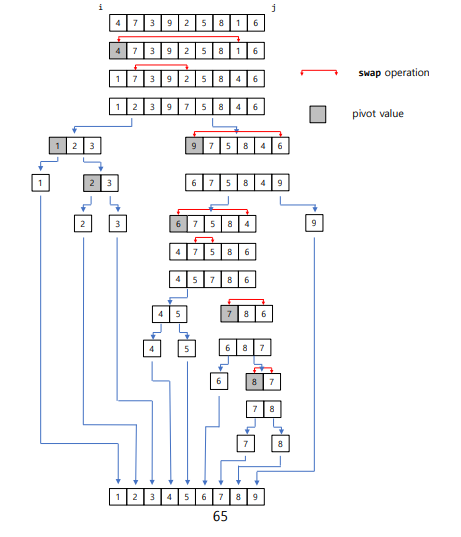
이거 해보기
- 왜 while문에서 등호를 붙이지 않는가

- 배열의 모든 숫자가 같으면 i,j가 계속이동
- 등호가 없으면 한 칸 이동후 멈추고 교환하고 중앙 부근에서 리턴되기 떄문에 범위체크도 필요없고 시간도 적당하게 멈춤
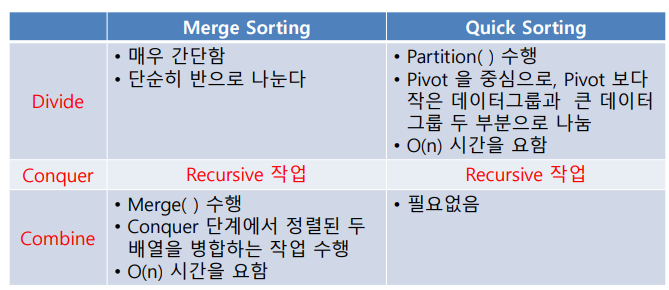
Merge vs Quick
Bolts & nuts

- 볼트 하나에 모든 너트를 끼워보고 그 볼트에 작은, 큰, 딱 맞는 너트를 나누고 꼭 맞는 너트를 가지고 모든 볼트에 끼워 볼트도 그 너트에 작은, 큰, 딱 맞는 그룹으로 나눔 그 이후로는 작은거끼리, 큰거끼리 재귀적으로 실행