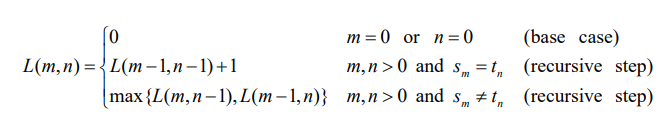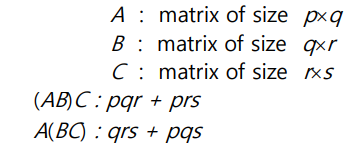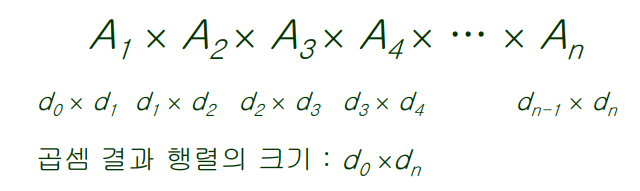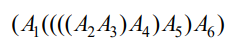동적계획법
- 분할 정복과 유사
- 문제를 여러개의 subproblem으로 나누고 각 서브문제를 해결 후 원래 문제의 해답을 구함
- 그러나 서브문제가 독립적이지 않고 서로 연관된 경우 매우 많은 반복 연산이 이루어짐
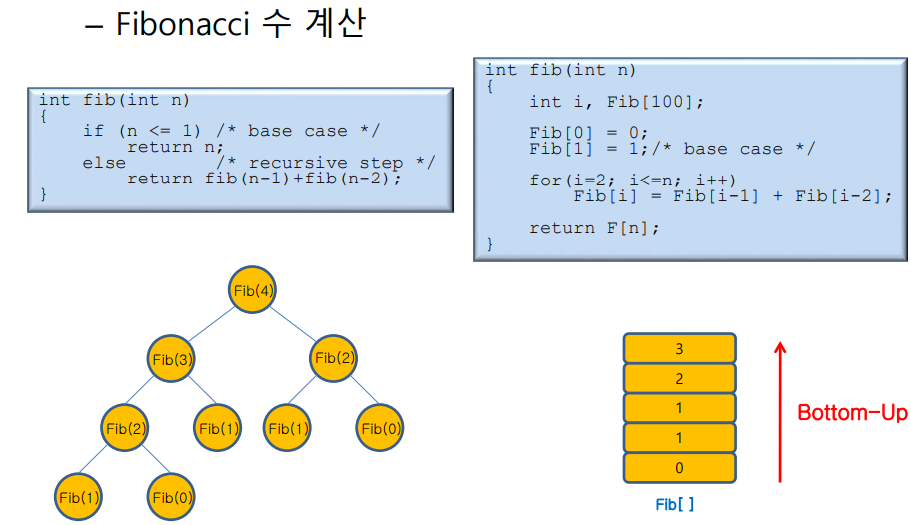
Fibonacci로 예시
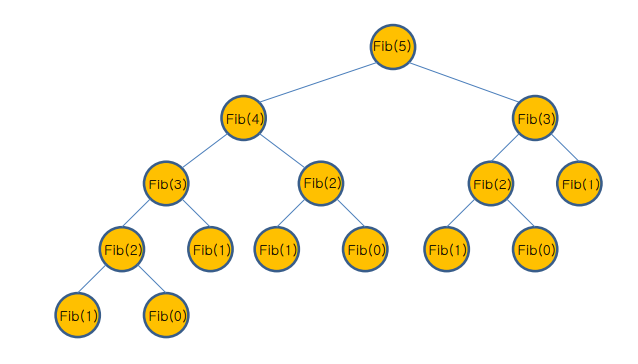
- fibonacci(5)를 구하기 위해 4,3이 필요한데 둘이 독립적이지 않음
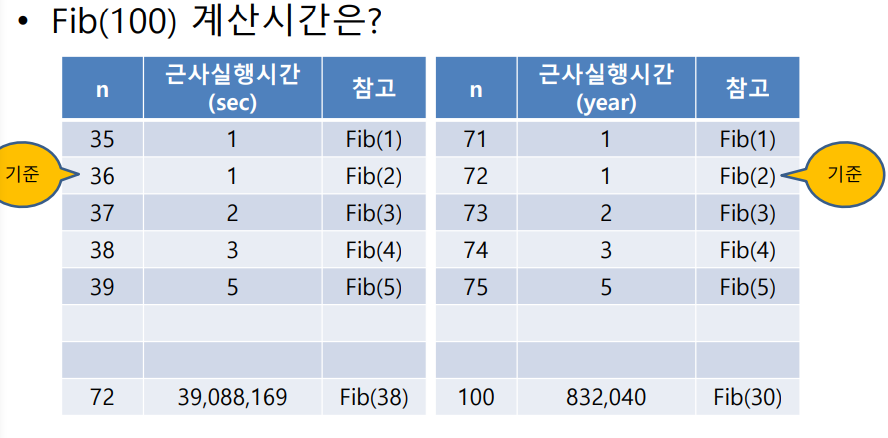
- 피보나치의 수와 실행시간이 근사하게 비례
- 피보나치 100을 구하는데 832040년이 걸림 fibo(30)에 해당하는 값
- 그래서 이런 무수히 많은 반복연산을 제거하기 위해 다이나믹 프로그래밍 사용
Memoization
- 재귀적으로 문제를 해결하면서 해결한 작은 문제의 해답을 테이블에 저장
- recursion베이스에 table로 해결된 문제의 해답을 저장하는 방법
- 동적계획법중 하나임
- 테이블은 문제가 해결되지 않았음을 나타내는 값으로 초기화시킴
Fibonacci by Memoization
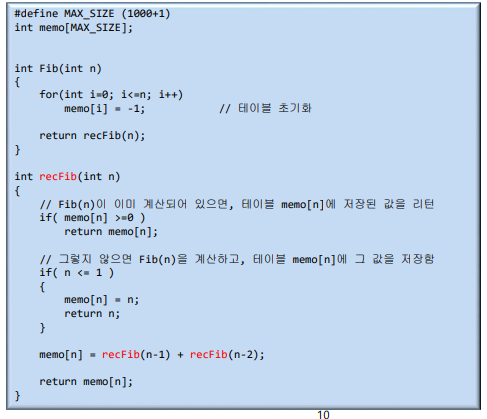
- 테이블에 값이 있으면(0보다 크거가 같으면) 그 값을 바로 리턴
- 초기화를 피보나치는 0보다 크기 떄문에 -1로 초기화했기 떄문에
반복 연산의 제거
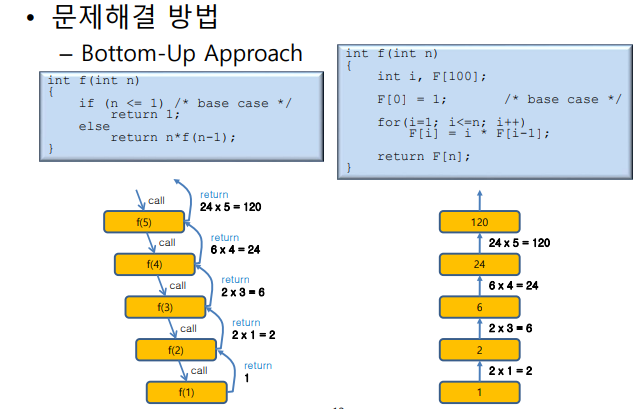
- Bottom up의 방식으로 작은 문제부터 해결하고 그 결과를 테이블에 저장
- 큰 문제를 해결하면서 작은 문제를 해결할 필요가 있는 경우에 테이블의 결과를 사용
Memoization과는 다르게 recursion베이스가 아닌 반복문을 사용
Bottom up
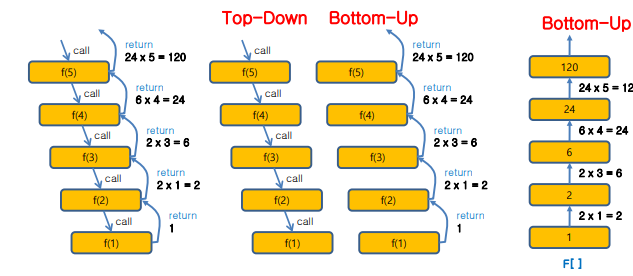
- 방향이 중요한게 아니고 큰 문제, 작은 문제중 어디서 시작하는지가 중요(TOP : 큰 문제, Bottom : 작은 문제)
- 팩토리얼 예시
동적계획법으로 해결하는 문제의 형태
- 거의 최적화문제
- 해답이 여러개 있지만 특정 조건이 최대 혹은 최소가 되는 해답을 구ㅏ는 문제
- 동전 교환 문제
동적계획법 문제해결 시나리오
- 최적의 해답의 구조를 분석
- 이때 working backward을 많이 사용
- working backward는 top down 방식
- 최적의 해답의 최적값을 재귀식으로 정의
- 상향식으로 최적값 계산
- 단계 2에서 정의한 재귀식으로 최적값을 상향식으로 계산
- 단계 3에서 최적값을 구하고 단계 4에서 최적해답을 계산
- 동전문제를 예시로 하면 최소동전의 개수가 최적값 동전의 구성이 최적해답
분할 정복과 동적계획
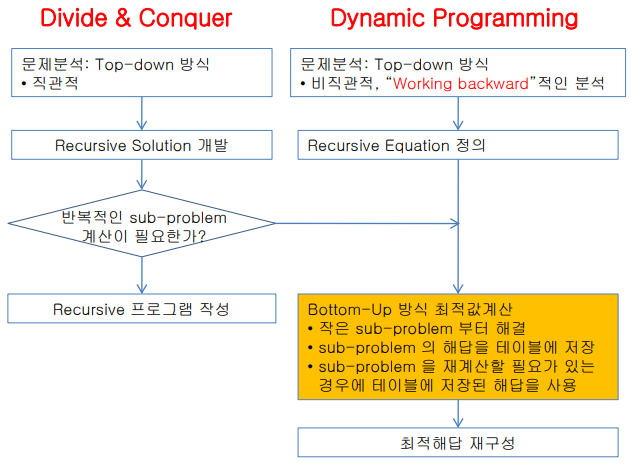
- 분할정복에서 반복적인 sub-problem계산이 필요하면 동적계획으로 빠질 수 있다
1차 동적계획법
- 재귀식에서 1개의 변수가 필요한 문제
- 1차원 배열로 동적계획 구현
- Fibonacci, 동전교환 문제 등
2xN 직사각형 타일 채우기
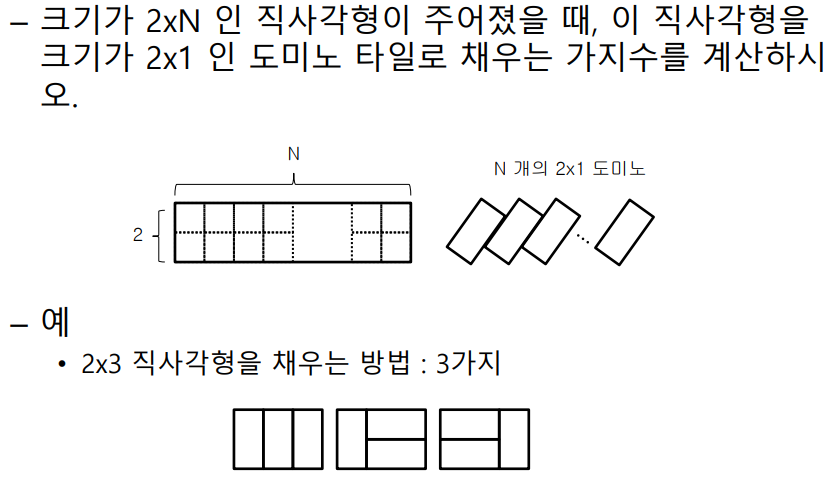
- working backword
- 직사각형 타일을 다 채워놓았다고 가정하고 빠져나갈때의 과정을 분석
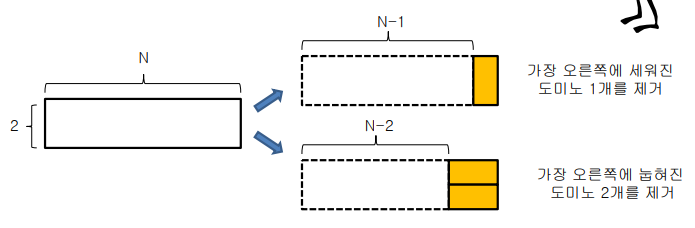
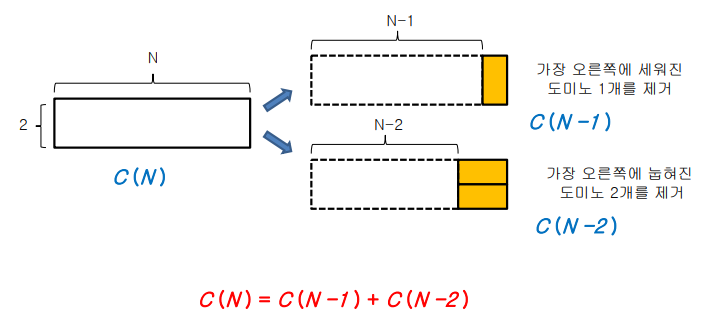
- 재귀식 작성
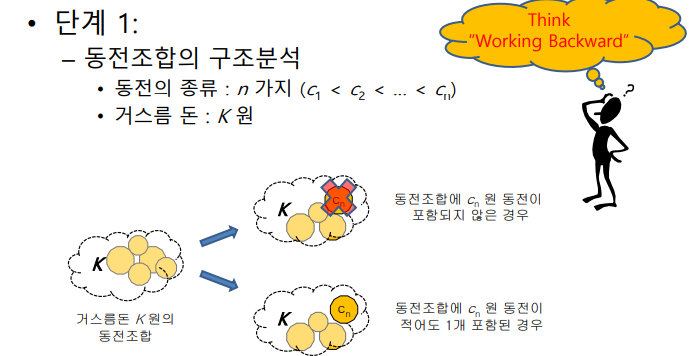
동전 교환

- working backword
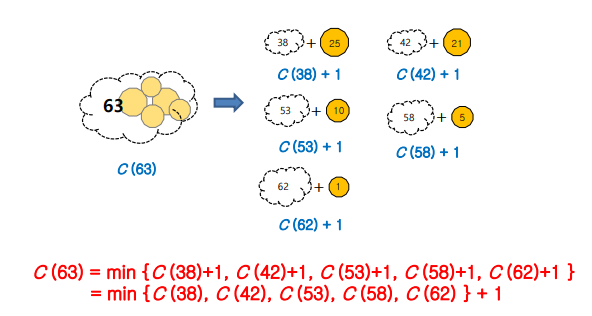
- 63원에서 시작해서 빼는 방식으로 생각
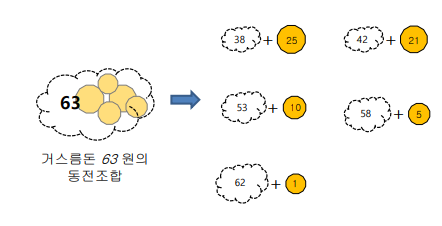
- 재귀식
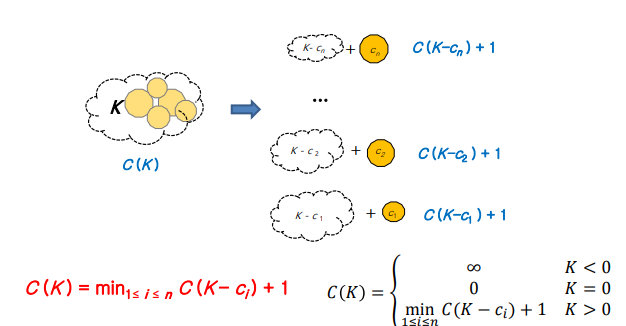
- K원을 바꿀때 최소 동전의 개수 : C(k)
- 남아있는 값보다 더 큰 값의 동전을 빼는 경우는 제외하기 위해 무한대로 베이스 케이스 설정해서 min에 안 들어가게 함
- 남은 값이 0원이면 정확하게 떨어진 것이기 때문에 베이스 케이스
- K원을 바꿀때 최소 동전의 개수 : C(k)
- k원을 바꿀때의 최소 동전의 개수 저장

- 배열에서 동전의 크기 만큼 인덱스를 뺀 값 중에서 최소값을 호출하는 방법으로 재귀
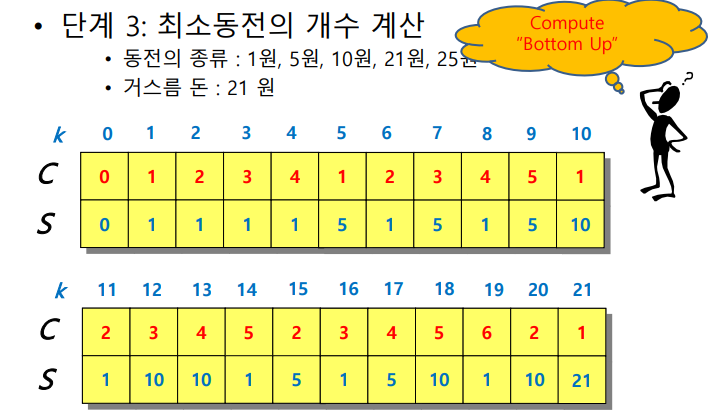
- 동전의 조합까지 알기 위해선
- 위에서 C[k]배열을 저장하는 과정에 S[k]에 마지막으로 선택한 동전을 저장해둠
- 개수만 똑같으면 순서는 상관이 없음
- 6원에서 1원뺴고 5원뺄 수 있고 5원빼고 1원 뺼수도 있다. C[1], C[5]둘다 값이 1이므로
- 마지막 동전 조합을 재귀식으로
2차 동적계획
- 재귀식에 2개의 변수가 필요
- 2차원 배열로 동적계획법을 구현
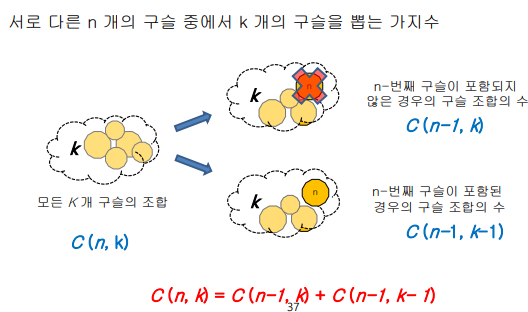
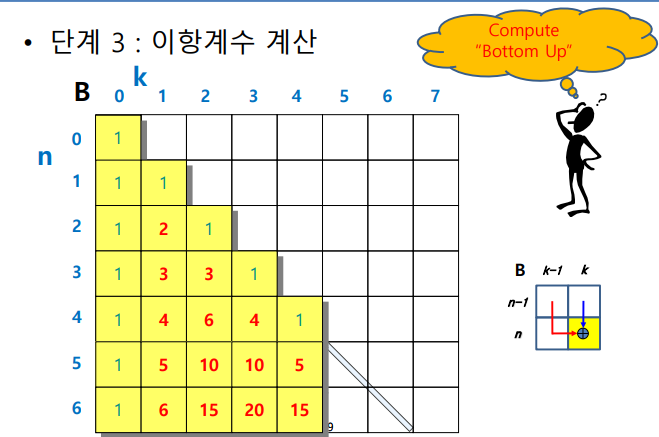
이항계수

- 위의 식을 그대로 사용하면 오버플로우 문제가 생김
- 파스칼의 재귀식
- k가 0개이거나 n개면 뽑는 경우의 수가 1임 이ㅓㄳ이 베이스 케이스
- 2차원 배열로 옮기기
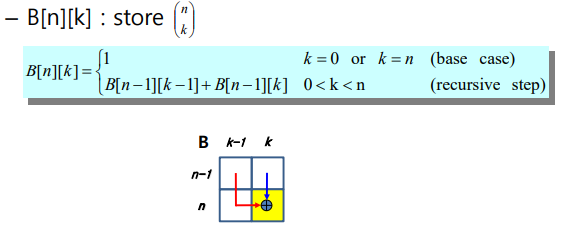
- 대각선과 첫 열은 베이스 케이스
동전교환 2
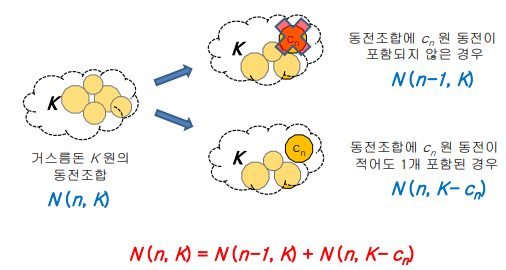
거스름돈을 교환해 주는 동전의 조합의 수

- 이항계수와 비슷
- n개로 k원을 만드는 방법은
- 베이스 케이스 세우기
- 거슬러 줄 돈이 음수거나 남은 값에 해당하는 동전이 없으면 가지수가 없는 경우임 0으로 설정해서 골라지지 않게함
- 거슬러 줄 돈이 0원일때 동전을 안 거슬러주는 가짓수 1가지로 베이스케이스를 1로 설정함
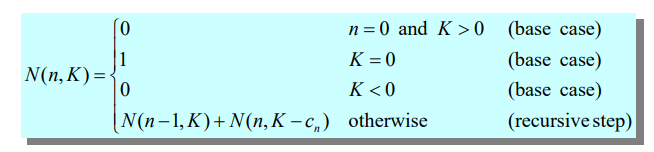
- 재귀식은 기계적으로 배열로 옮길 수 있음
- 위의 재귀식으로 배열을 bottom-up방식으로 채워줌
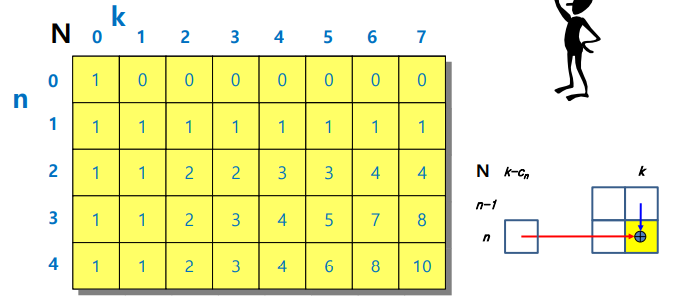
- 한칸의 값은 n-1에있는 값과 k에서 k-n값을 더한 값
중간고사
Longest Common Subsequence
(최장 공동 부분수열)
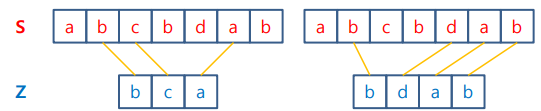
- 공통
- 두개의 스트링의 길이가 가장 긴 공통 부분 수열을 구해야 함
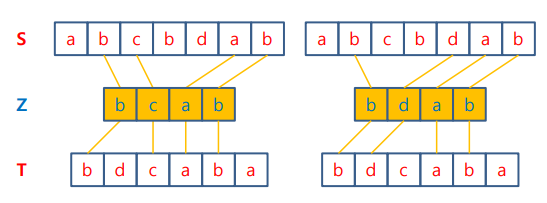
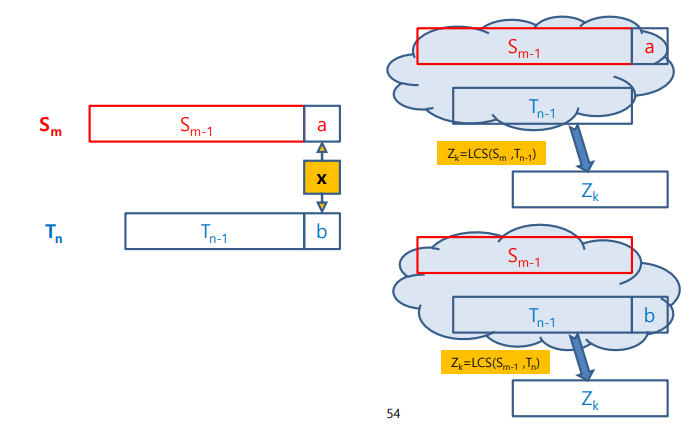
- working backword : 맨 뒤의 문자부터 비교, 같으면 해당 문자가 두 스트링의 최대공통부분 수열의 마지막에 반드시 들어가야 함
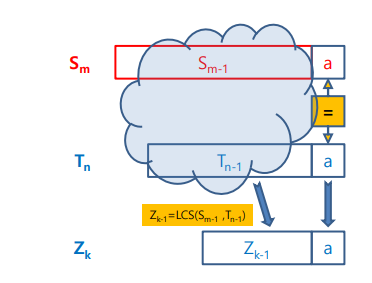
- a를 lcs의 마지막에 추가하고 lcs(k-1)을 s와t에서 마지막을 제거한 부분에서 구함
- 마지막의 문자가 다를 경우 s는 그대로 t를 하나 제거 하거나 t를 하나제거 s는 그대로 둔 문자에서 z(k)를 구해야함
- 재귀식
- L테이블에 길이를 저장
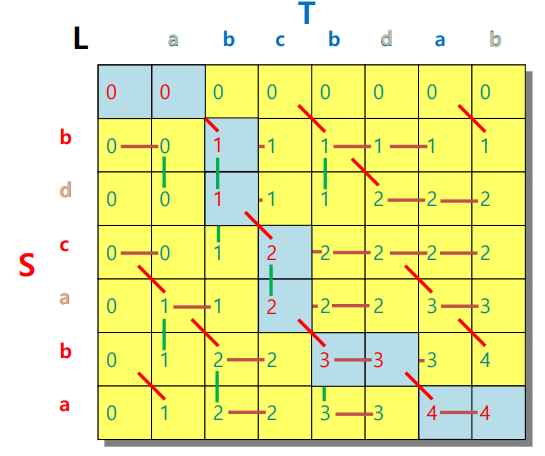
- T,S가 0이면 표도 0(base case)
- T,S에 있는 문자가 같으면 왼쪽 대각선의 값에 1을 더해서 가져오고 다르면 왼쪽, 위중 더 큰 값을 가져옴
- 추가로 S테이블에 어디서 가져온 값인지 저장해둠
(L에선 길이를 구하고 S에서 조합을 구함) - 제일 오른쪽 밑에서 역으로 왔던길을 따라가면 LCS를 구할 수 있음
- 왔던길은 S테이블에 0,1,2로 표시해둘 수 있음
Chained Matrix Multiplication

- A행렬 pxq와 B행렬 qxr을 곱할때 곱셈 연산의 수는 pxqxr
- 행렬이 3개이상일때 결합법칙이 성립하기 때문에 곱셈 연산의 횟수가 다르게 만들 수 있음(같은 결과를 내면서도)
- 행렬이 n개일경우 행렬의 크기를 나타내는 변수는 n+1개가 있음, 곱셈 후 최종 결과 행렬의 크기는 d0 x dn이 된다
- 마지막에 곱할때(2개가 남았을때)의 최소 횟수를 선택


- i와 j가 같으면 곱할 행렬이 1개라는 뜻이므로 베이스케이스, 0임
- 배열이 2개일떄는(j-i가 1일때)는 1개의 바로 위의 대각선임
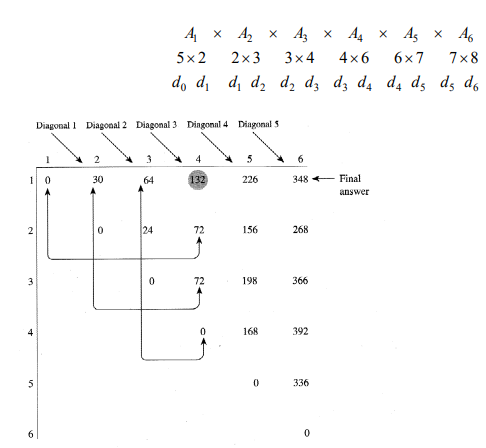
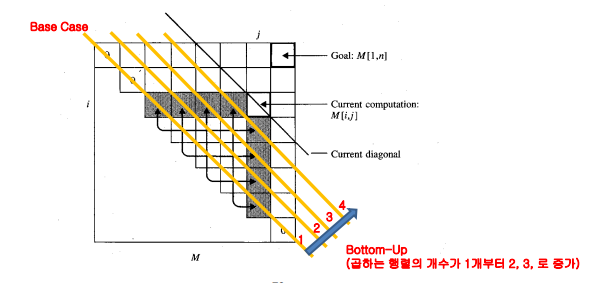
- 0부터 채우고 대각선으로 채움
- 행렬이 2개인 경우도 바로 계산함
- 3개는 2개 곱한거 횟수에 남은 하나 곱합 횟수를 더한 모든 경우의 최소값
- K[1][4] = 132를 구하는 과정
- 1,2,3,4를 곱할때 1에서2에서3에서 각각 자를 수 있음
- 자른 경우에 따라 본인의 왼쪽에 있는 것과 밑에 있는 것중 골라서 더하게 됨
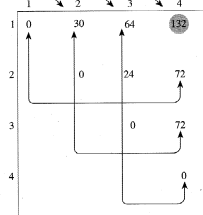
- 0+72, 30+72, 64+0
- 위의 3개에 자른 2개를 곱해서 합치는 횟수를 더해주어야 함
- 0+72는 1x(2x3x4)이므로 5x2x6번을 더함 : 132
- 30+72는 (1x2)x(3x4)이므로 5x3x6을 더함 : 192
- 64+0은 1x2x3x(4)이므로 5x4x6을 더함 : 184
- 추가로 각 횟수를 구할때 짜르는 위치를 P테이블에 저장함
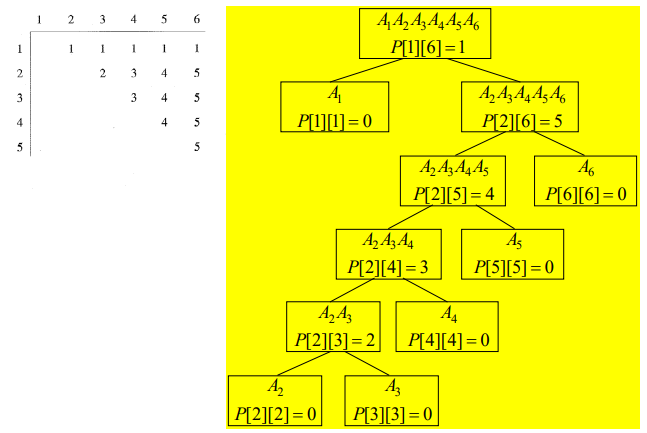
- P를 활용해서 재귀적으로 곱하는 순서를 출력