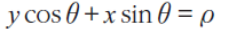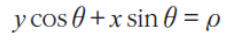선분 검출
에지의 연결과 표현
- 에지를 끝점, 분기점, 통과점으로 분류
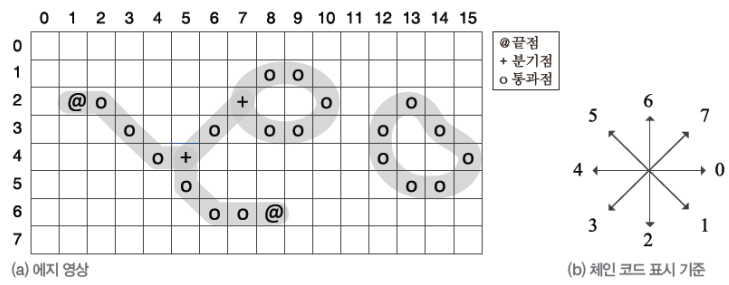
- 엣지를 끝점과 분기점으로 나누어 엣지 토막으로 나눔
- 추가로 체인코드로 시작점만을 가지고 중간의 통과점을 방향만 나타내면 전체 영상에서 엣지를 효과적으로 표현 가능

- 선분근사

- h가 임계값 이내가 될 떄까지 선분 분할을 반복해 직선으로 만드는 것
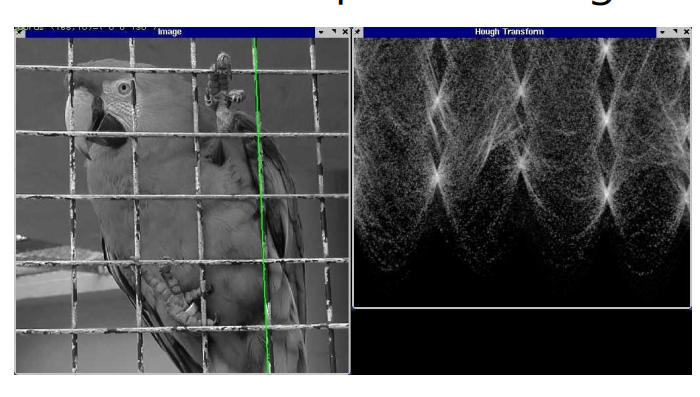
허프 변환
- 위의 에지의 연결 과정을 생략하고 선분을 검출
- 엣지의 정보를 직선의 방정식으로 표현하는 것
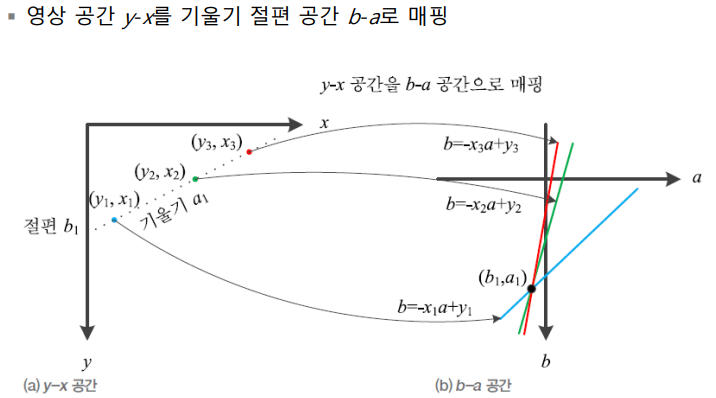
- 영상의 x,y(special domain)를 기울기와 y절편으로 변환
- 기울기가 y좌표와 수평일떄 문제가 생겨 극좌표계(삼각함수)로 표현
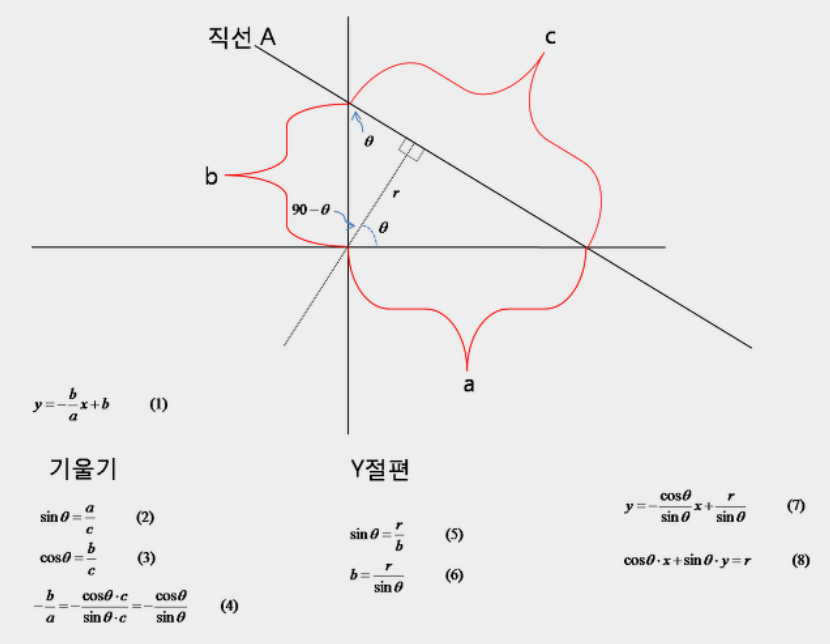
- 1의 직선의 방정식을 8로 변환
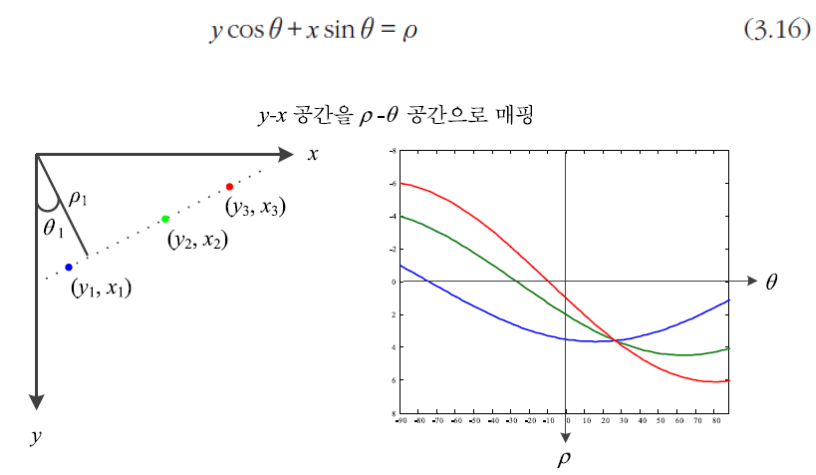
- 3개의 좌표가 만나는 지점이 직선의 방정식을 의미함
- 극좌표계를 사용하여 차원을 줄이고, 엣지가 끊어져 있는 경우에도 검출 가능함
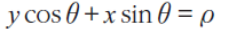
- 위의 식에서 x,y는 엣지의 좌표값, 세타값을 변화시켜 직선을 찾는것임
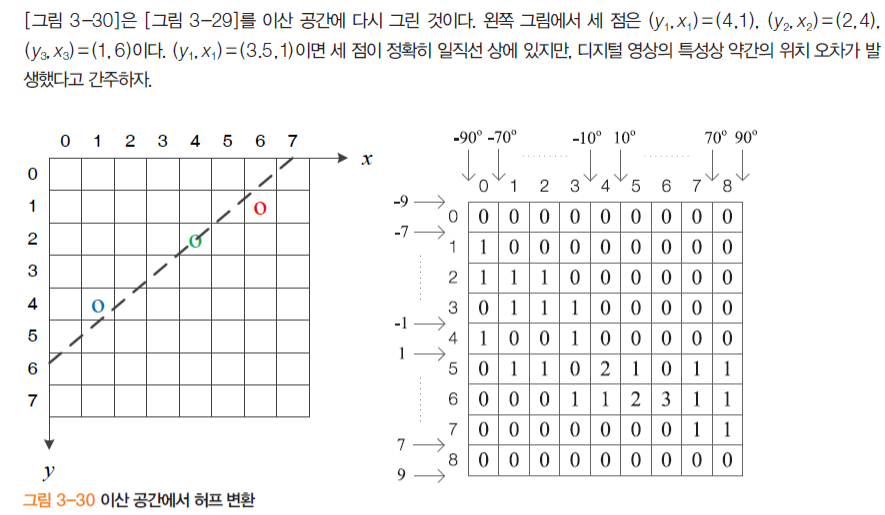
- 위의 3점을 나타내는 직선을 찾는 문제가 허프 변환
- 이 식을 동일하게 사용
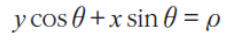
- 파란색점부터
- y=4,x=1를 식에 대입하면 4cosθ + sinθ = r
- = -4
- θ를 -90부터 대입해서 나오는 값에 1을 추가해줌
- 3점을 모든 각에서 하고
- 3점이 모두 만나는 지점에서의 세타와 r이 직선의식
- ycos30 + xsin30 = 3인 지점
영상에서의 여러 점을 극좌표계로 표현해 모든 점이 모이는 좌표에서의 θ,r값을 사용해 직선의 방정식으로 표현
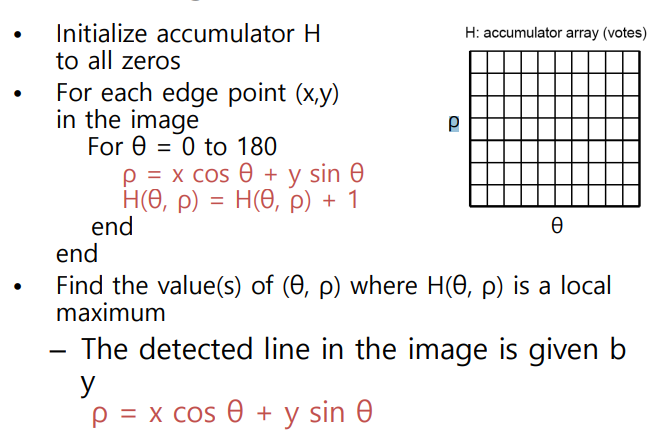
허프변환 알고리즘
- ρ,θ를 어느 단위로 나누는지에 따라시간과 정확도가 달라짐
- 각각의 엣지에 대해서 0부터180까지 세타값을 대입해 ρ값을 구하고 이를 해당하는 극좌표계의 좌표에서 1을 더함
- 극좌표계 배열에서 모든 점이 위치하는 곳의 ρ,θ를 사용해 직선의 방정식으로 표현
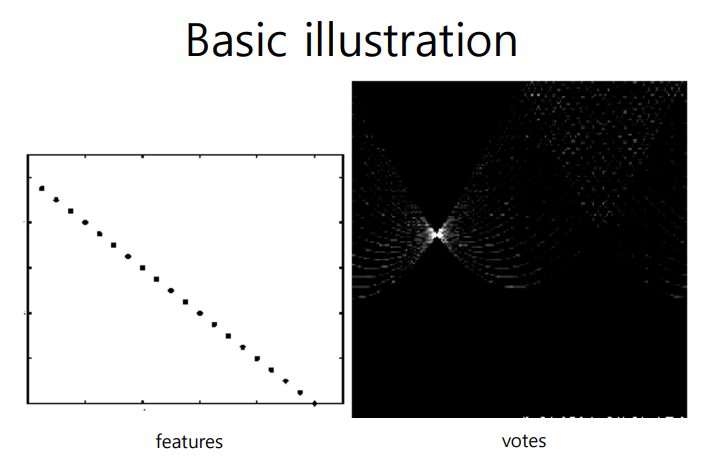
- 각각의 끊어진 점을 가지고도 직선의 방정식을 구할 수 있고 2차원의 배열로 표현해 차원을 줄이는 장점이 있음
- 도형의 표현
- 정사각형의 경우 직선이 4개가 필요

- 같은 기울기가 2개씩 나타남
- 원의 경우 직선이 없어 모이는 점이 없음
- 가장 밝은 점은 가장 긴 직선을 나타냄
- 여러개의 직선
- 약간의 오차가 있는 경우(주변에 모이기는 하지만 한점에서는 모이지 않을떄)
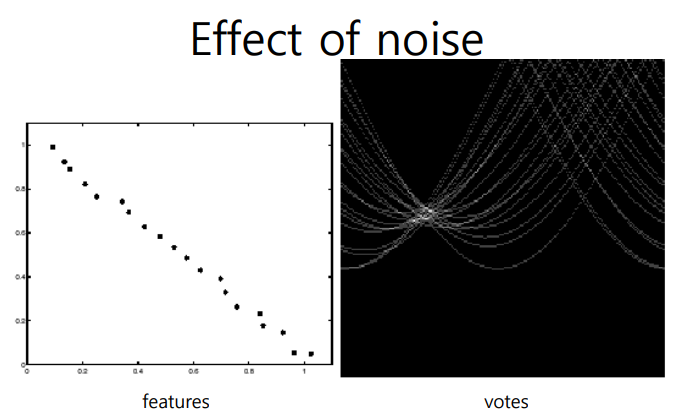
- 특정 수치 이상을 뽑아 그 좌표들의 평균을 사용하기도 함
- 점들이 완전히 랜덤일때는 특정할 직선을 찾을 수 없음
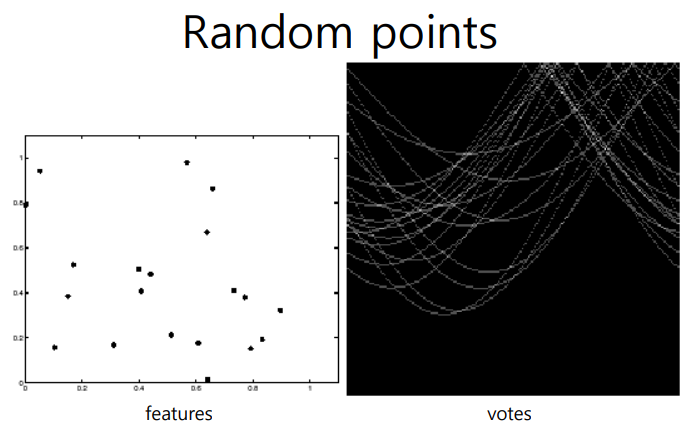
- 특정 범위 이상으로는 점들이 모여 있어야 사용가능함
- 허프 변환으로 원의 반지름 찾기
- 엣지를 검출하는것 까지는 동일
- 직선에서의 세타 대신 r을 사용 r은 a와b사이의 값이 라고 가정하고 a~b를 대입함
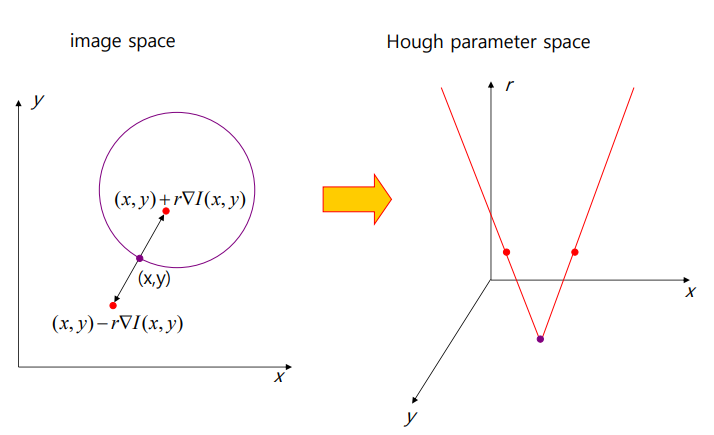
- 엣지를 기준으로 양쪽으로 r만큼 떨어진 직교하는 2점을 보팅
- 모든 엣지에서 모든 r값으로 진행 했을때 가장 많은 점이 보팅되는 지점이 원의 중심
- 어떤 물체의 중심점을 찾는데 사용가능
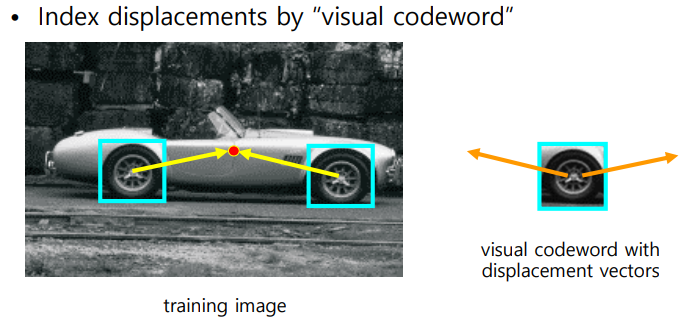
- 물체에 어떤 특징점을 기준으로 여러 방향으로 보팅시키고 공통적으로 모이는 점을 물체의 중심으로 생각할 수 있음
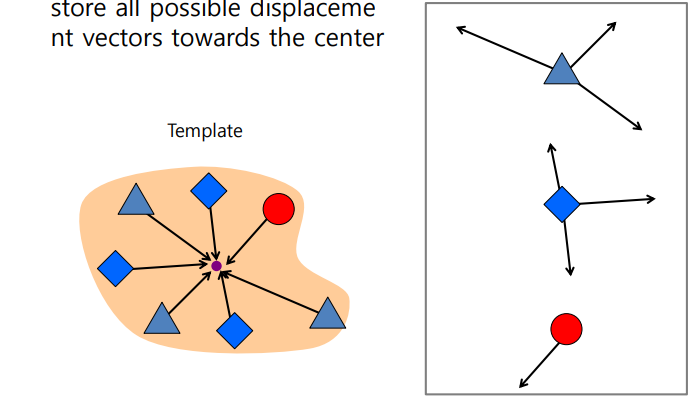
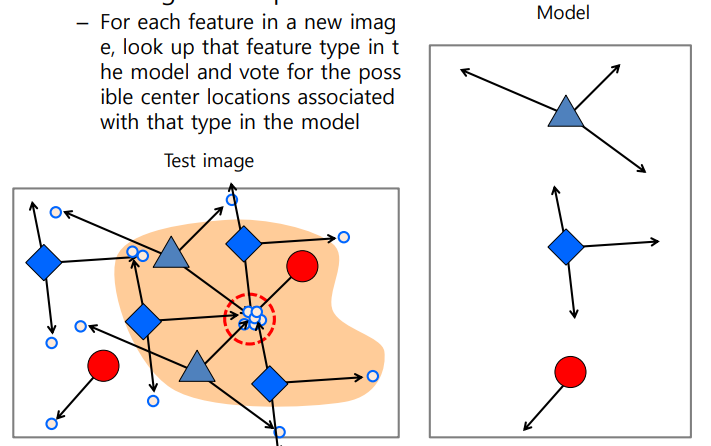
- 자동차의 앞,뒷바퀴에서 동일한 방향으로 보팅할때 앞,뒤중 만나는 점이 자동차의 중심
- 여러 부품에서 중앙을 찾늘수 있음
- 부품들을 가지고 전체적인 자동차를 인식하는 방법 -> bottom - up은 자동차의 일부분이 가려져도 그 물체를 자동차로 인식시킬 수 있음
허프 변환 장, 단점
- 장점
- 물체가 부분적으로 가려져도 처리 가능
- 차원을 줄임(허프 배열으 통해)
- 단점
- 시간이 오래걸림
- 적절한 그리드 크기 선택이 어렵고 의미 없는 점이 발생할 수도 있음 ///
RANSAC
- 직선의 방정식을 찾을때 잡음을 처리할 수 있게 만들어 주는 알고리즘
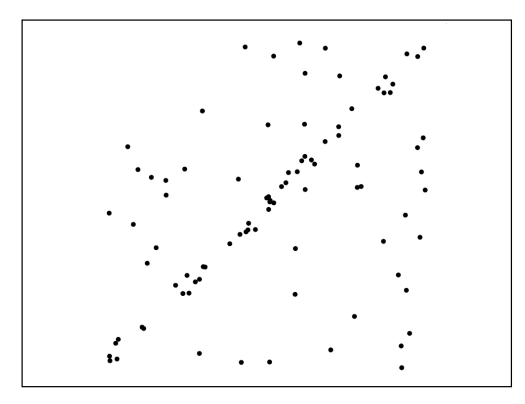
- 아웃라이어를 고려하면 서로 다른 많은 직선이 나올 수도 있음
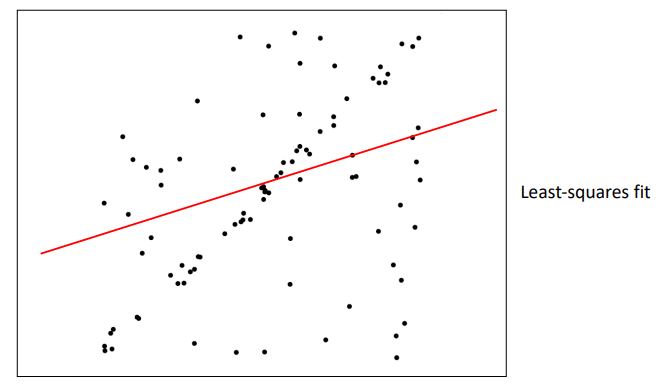
- 모든 점을 고려한 직선(아웃라이어도 고려함)
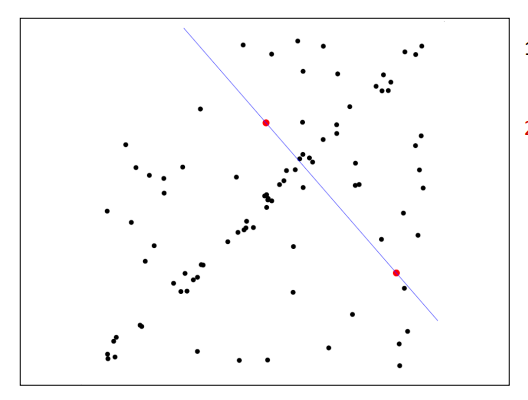
- 먼저 랜덤한 점 2개를 고르고 2개로 직선을 만듦
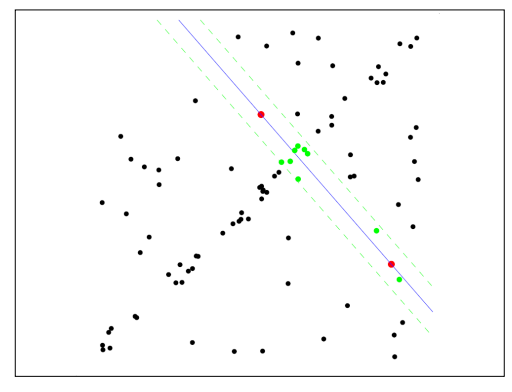
- 그리고 직선에서 마진을 주고 그 안에 다른 점이 몇개가 들어오는지 구함
- 마진 안에 들어오는 점의 개수가 원하는 수를 넘을때까지 2점을 뽑고 직선을 구하고 마진안에 들어노는 점의 수를 구하기를 반복함
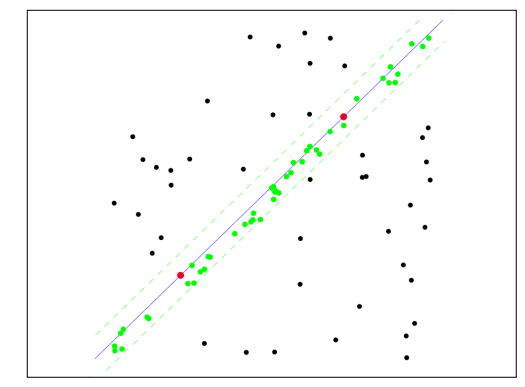
- 우연히 고른 두점의 직선에서 마진안에 원하는 수 이상의 점이 들어온 경우임