개인스터디
통계야 놀자 1회차
✅ 이번 수업에서 배우는 것
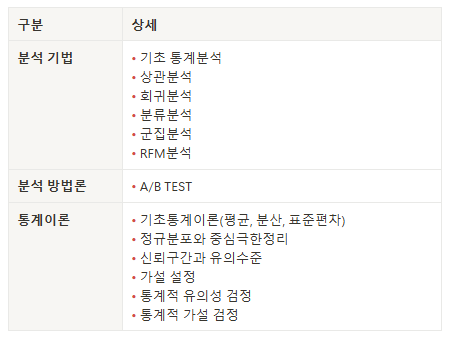
✅ 왜 데이터 종류를 분류할까?
- 분석 방법, 시각화 방식, 통계 모델 결정에 중요한 기준이 됨
- 데이터 종류에 따라 분석 기법이 달라짐
대표값
WHERE 어디에 존재하는가
- 평균
- 값들의 총합 ÷ 개수
df['어쩌구'].mean()
- 중앙값
- 중간에 위치한 값
df['어쩌구'].median()
- 최빈값
- 가장 많이 나온 값
df['어쩌구'].mode()
편차, 분산, 표준편차
HOW 어떻게 존재하는가 = 얼마나 퍼져있는가
편차
개별 값 - 평균
각각의 값 이 평균으로부터 얼마나 떨어져 있는가
편차들을 더하면 항상 합이 0
→ 평균을 기준으로 좌우에 퍼져있기 때문
→ 평균만으로 값들이 퍼진 정도를 파악하기 어려움
분산
편차²의 평균
전체 값 이 얼마나 퍼져있는가
대표적인 값으로 평균을 쓰는데 0이 나와서 정확히 볼 수 없으니까 분산이라는 개념이 추가됨
- 이해하기 쉬운 예시
데이터1 = [30, 70, 80] 평균 60
데이터2 = [20, 60, 100] 평균 60두 데이터셋 모두 평균은 같으나 같은 데이터가 아님
(데이터 2가 훨씬 흩어져 있음)
→ 하나의 숫자로 '다르다'고 표현하기 위해 '분산'이 필요
표준편차
분산의 제곱근 → 다시 단위 맞추기 standard deviation(σ)
- 단위를 왜 맞춰야 할까?
편차에 제곱을 하면 단위가 커지고 왜곡됨
→ 실제 단위로 해석하기 위해 단위를 맞추는 거
모집단, 표본, 표본분포
편향 최소화
모집단
전체 데이터 집합
표본
모집단에서 뽑은 일부
표본분포
표본이 흩어져 있는 정도
(+) 표본평균의 분포
여러 표본 평균의 분포
중심극한정리에 의해 정규분포를 따름
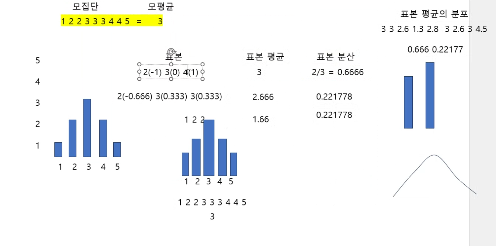
(+) 표준오차 = 표본평균의 오차 범위
도수분포표 & 히스토그램
- 도수분포표 : 각 값에대한 도수와 상대도수를 나타내는 표
- 도수: 특정 구간(=계급)에 속하는 데이터 개수
- 상대도수: 전체 대비 비율
→ 시각화는 히스토그램 사용
정규분포
데이터 범위가 클때, 머신러닝 성능 향상을 위해 표준화 필수
평균을 중심으로 좌우 대칭인 종 모양 분포
평균 0, 분산 1 → 표준정규분포
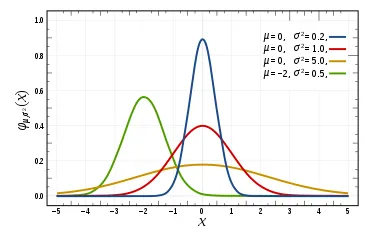
정규분포 🔴🟡🟢🔵
표준정규분포🔴
- 표준정규분포가 왜 필요할까?
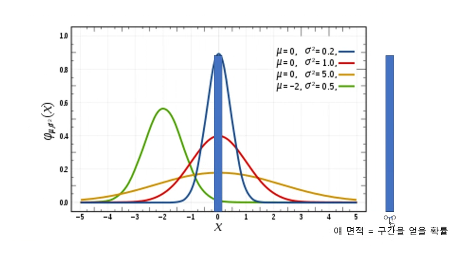
곡선 아래 면적 = 확률
정규분포에서 어떤 값이 나올 확률을 계산하는 게 복잡한데 그걸 간단하게 하기 위해서 필요함
-
표준화(Z-score)
모든 정규분포를 표준정규분포로 바꾸는게 표준화!z = (확률변수 x - 평균 m) / 표준편차
신뢰구간, 신뢰수준
신뢰구간
모수가 포함될 것으로 예상되는 값의 범위
신뢰수준
신뢰구간이 모수를 포함할 확률(보통 95%, 99%)
-
신뢰수준 ↑ → 신뢰구간 넓어짐 → 정확도 ↓
-
이해하기 쉬운 예시
- "오늘 날씨는 맑거나, 흐리거나, 비오거나, 눈오거나"
신뢰수준 80% > 정확도↓ - "오늘은 태풍이 오다가 갑자기 저녁에 맑아집니다"
신뢰수준 10% > 정확도↑
- "오늘 날씨는 맑거나, 흐리거나, 비오거나, 눈오거나"
-
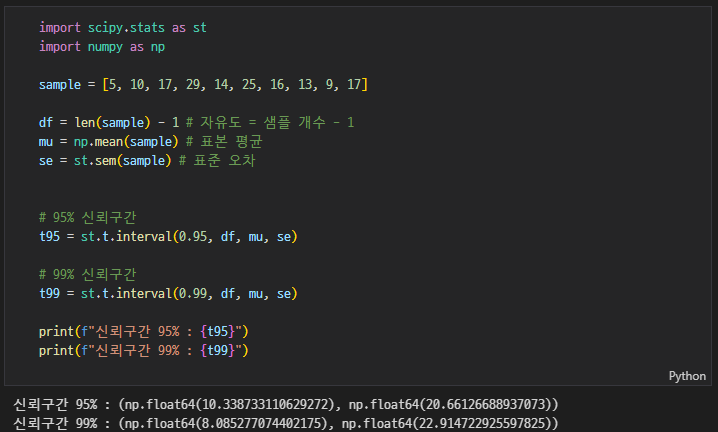
scipy 활용
☑️ 요약
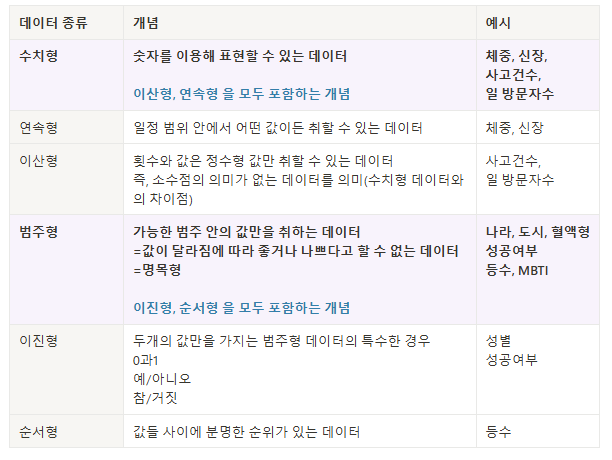
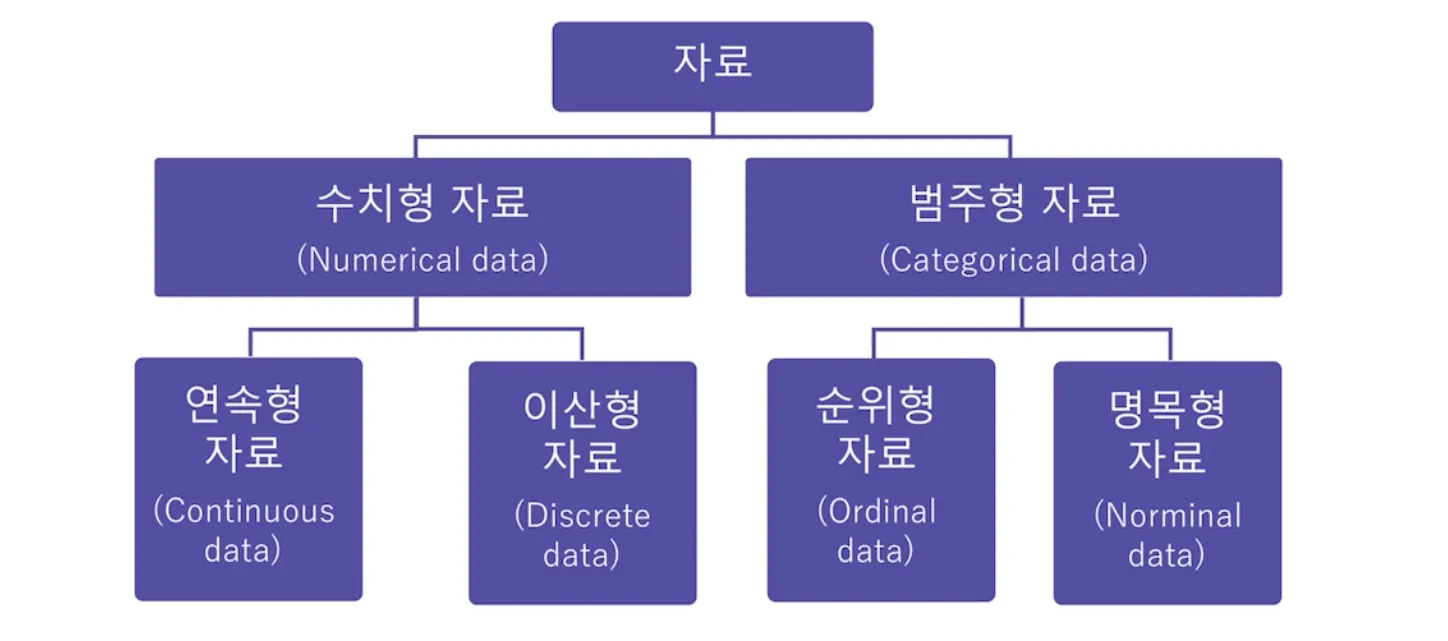
- 데이터는 대표적으로 수치형 / 범주형으로 나뉘며, 종류에 따라 분석 방법이 다름
- 대표값은 평균, 중앙값, 최빈값
- 분포를 명확히 파악하기 위해 편차 → 분산 → 표준편차
- 표본분포로 모집단 추정
- 정규분포는 종 모양, 좌우 대칭
- 표본평균이 정규분포를 따른다 = 중심극한정리
- 신뢰구간/수준은 결과 해석의 불확실성을 수치화함
- 서로 다른 단위의 데이터를 동일 선상에서 비교할 때 표준화 필수

갓동진님께 감사를..
통계학 기초 2주차
모집단과 표본
- 모집단(population) : 전체 집단
- 표본(sample) : 모집단에서 추출한 일부
표본을 사용하는 이유
- 비용과 시간 절약
- 접근성 문제
전수조사가 현실적으로 어려움 - 대표성 있는 표본으로 모집단 전체 추정 가능
- 데이터 처리 용이
예시
- 도시 연구 : 100가구 전력 사용량으로 전체 추정
- 의료 연구 : 일부 환자로 치료 효과 검토
- 여론조사 : 유권자 표본으로 선거 결과 예측
표본오차와 신뢰구간
- 표본오차 : 표본 통계량과 모집단의 실제 값 차이
- 표본이 클수록 표본오차 ↓
- 무작위 추출로 오차 최소화(공평하게)
- 신뢰구간 : 모집단의 값이 포함될 범위
- 95% 신뢰수준 → 평균 ± 1.96(z) × 표준오차
실습
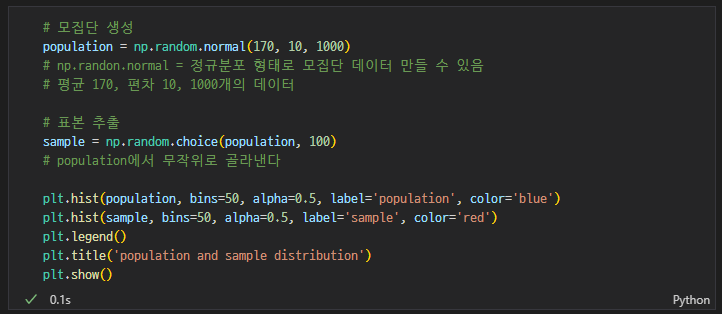
- 코드 설명
np.random.normal(loc=0.0, sclae=1.0, size=None)정규분포 형태로 모집단 생성
(평균, 표준편차, 개수)np.random.choice(array, size, replace = True, p=None)
(원본배열, 출력배열크기, 복원추출여부, 선택될 확률)
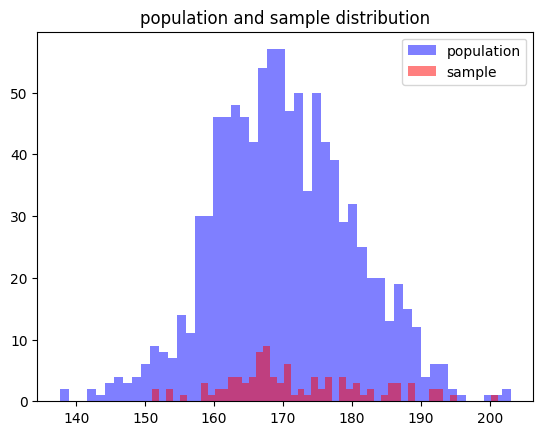
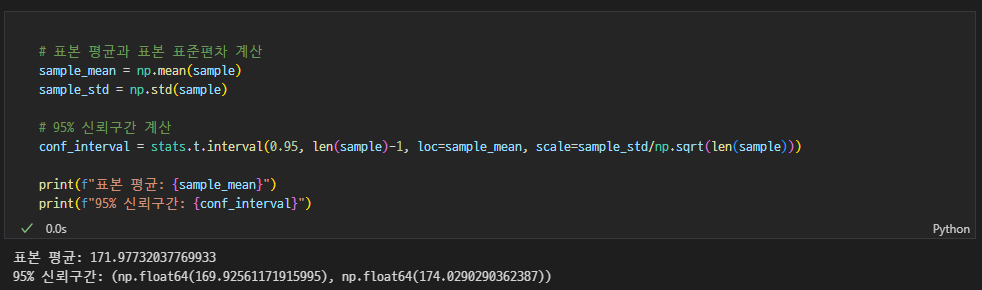
- 코드 설명
scipy.stats.t.interval(alpha, df, loc=0, scale=1)
(신뢰수준, 자유도, 표본평균, 표준오차)- 자유도 = 표본 크기 - 1
- 표준 오차 = 표준 편차 / 표본 크기 제곱근
정규분포✅
가장 기본적인 분포
- 종 모양의 대칭 분포
- 대부분의 데이터가 평균 주변에 몰려 있음
- 키, 몸무게, 시험 점수 등 다양한 자연현상에서 관찰
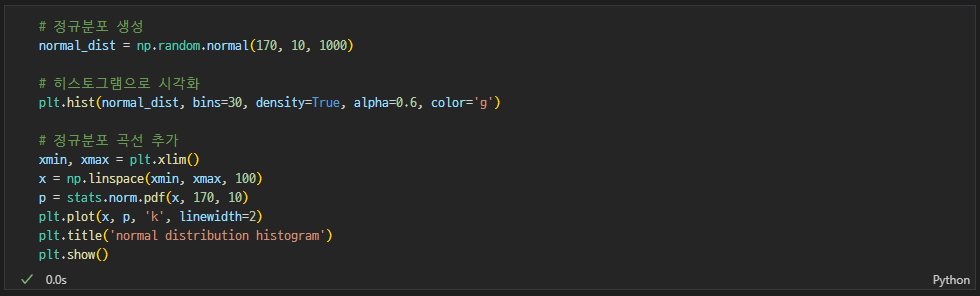
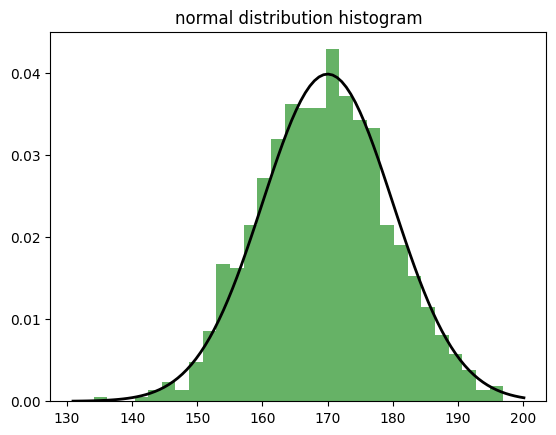
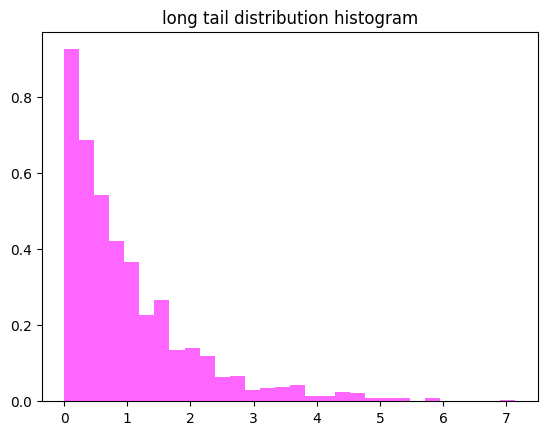
긴 꼬리 분포(롱테일)
소수가 큰 영향을 주는 비대칭 분포
- 분포 한쪽에 데이터가 몰리고 다른 쪽에 긴 꼬리
- 소득 분포, 웹사이트 방문자 수, 도서 판매량
- 파레토 분포, 멱함수 등 포함

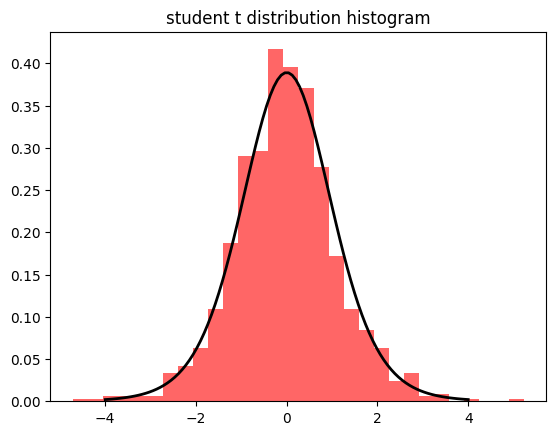
스튜던트 t분포
표본 수가 적을때 사용
- 표본 크기가 작을때(일반적으로 30 미만) 평균 비교 등에 사용
- 표본 수가 많아지면 정규분포에 수렴
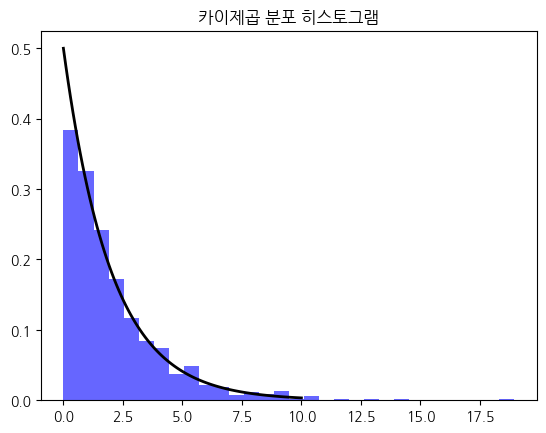
카이제곱 분포
범주형 변수의 독립성/적합도 검정에 사용
- 자유도에 따라 모양이 달라짐
- 독립변수가 완벽하게 서로 다른 질적 자료일때 활용
- 표본 수가 많아지면 정규분포에 수렴
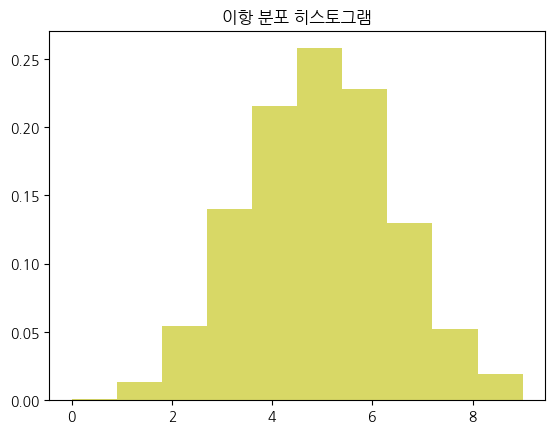
이항분포
결과가 2가지(성공/실패)인 실험의 반복
- 예시) 동전 던지기, 불량률 테스트
- 이산형 분포(연속 아님)
특정 정수값만 가질 수 있기 때문 - 표본 수가 많아지면 정규분포에 수렴

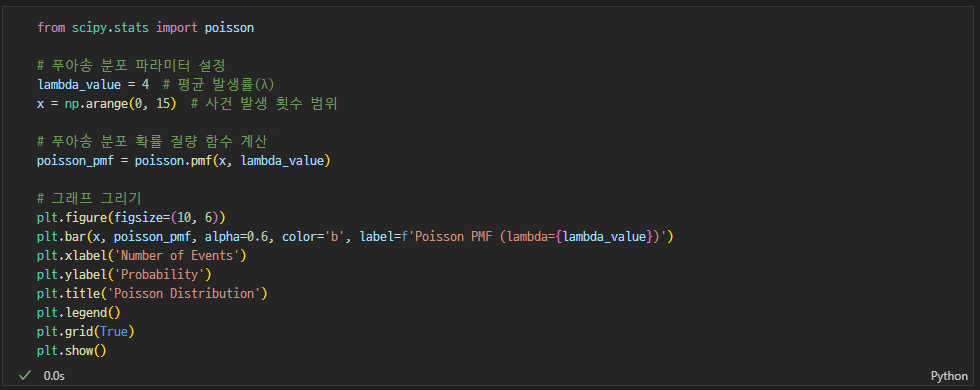
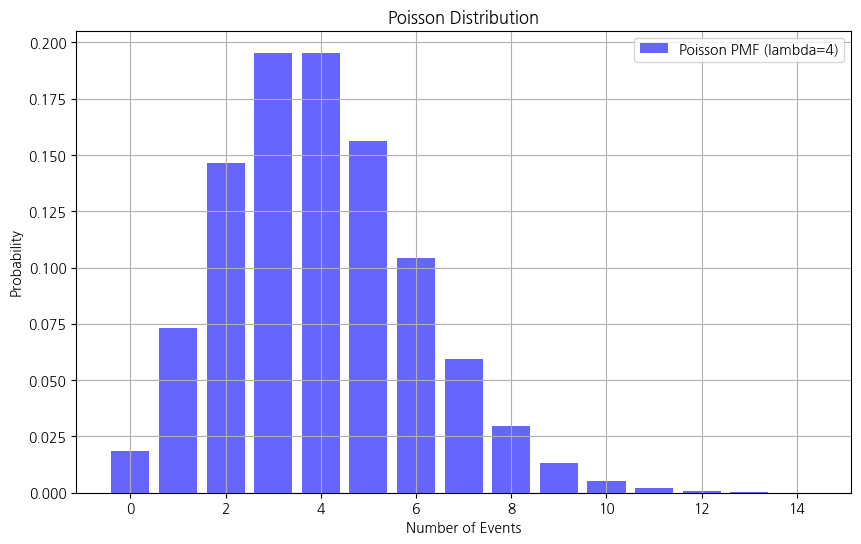
푸아송분포
일정 시간·공간 내 희귀한 사건 발생 수
- 예시) 시간당 콜센터 전화 수, 교통사고 수
- 이산형 분포(연속 아님)
- 평균 발생률 λ(lambda) 사용
- lambda가 커질수록 정규분포에 수렴
분포 정리☑️
| 상황 | 사용 분포 |
|---|---|
| 데이터 수 충분 | 정규분포 |
| 데이터 수 적음 | t 분포 |
| 소수가 큰 영향 | 롱테일 분포 |
| 범주형 독립성/적합도 검정 | 카이제곱 분포 |
| 성공/실패만 존재 | 이항분포 |
| 특정 시간·공간 내 발생 수 | 푸아송 분포 |
⚠️ 데이터가 많으면 대부분 정규분포로 수렴 (중심극한정리)
⚠️ 롱테일 분포는 데이터가 많아도 정규분포가 아님!
연습문제
어떤 표본의 평균이 50이고, 표본 표준편차가 10인 경우, 95% 신뢰구간을 구하세요. (표본 크기는 25로 가정)
- 95% 신뢰구간은 표본 평균 ± (1.96 * 표본 표준오차)로 계산됩니다.
- 표본 표준오차는 표준편차를 표본 크기의 제곱근으로 나눈 값입니다.
-
t분포 기반 풀이
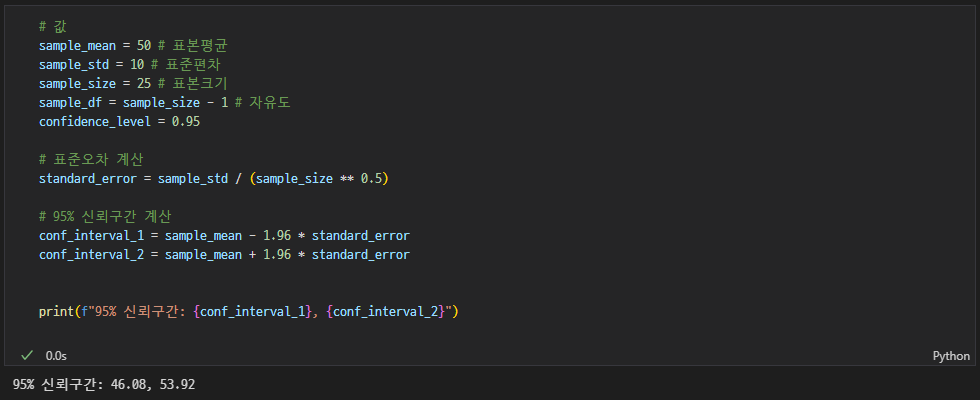
-
정규분포 기반 풀이
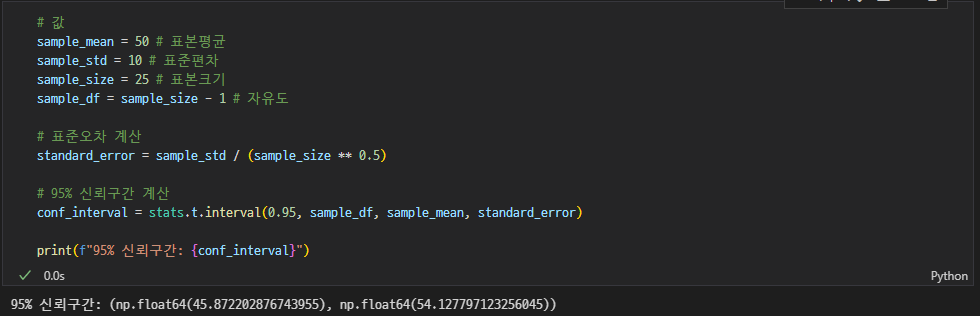
문제에서 정규분포 활용하라는 조건을 줬기 때문에 정답은 정규분포 기반으로 나온 값이 맞음
두 차이가 뭔지 현지튜터님께 여쭤봐서 정리해보자면
- 정규분포, t분포가 결국 다르기때문에 값에서 차이가 나는 것
- 표본의 크기가 작을수록 꼬리가 두꺼워진다 > t분포
이것 또한 표본의 크기가 커질수록 정규분포에 근사해짐 - 크기가 충분히 크면 정규분포 방식으로,
표준편차를 모르면 t분포 방식으로 사용하는 게 좋고
t분포가 좀 더 정확한 방식임
코드카타
SQL - 자동차 대여 기록에서 장기/단기 대여 구분하기
SQL - 자동차 평균 대여 기간 구하기
Python - 행렬의 덧셈
Python - 직사각형 별찍기
일기
- SQL
코드카타 62-63✅ - Python
코드카타 37-38✅ - 통계
기초강의 2주차✅기초강의 3주차❌세션 1회차✅
통계가 너무 어렵다😭 표'준', 표'본',오차,편차 이런 말들이 아직 헷갈리게 느껴짐 동진님이 세션 끝나자마자 또 떠먹여주셔서 조금 가닥은 잡혔는데 완전히 정확하게 정립되진 않은 것 같아서 복습하는 데 오랜 시간이 걸렸다
그래도 세션 듣고 비슷한 내용의 강의 들으니까 한번 더 복습하는 느낌이라 좋았음 코드로 그리는 건 또 새로운 문제다 보니 전체적으로 진도 나가는게 느렸다
내일은 3주차 강의 듣고, 1회차 세션 다시 복습하려고 한다!
오늘도 동진님께 샤라웃을 바칩니다.. 고맙습니다
