이진탐색

주어진 리스트에서 특정 데이터를 찾으려고 한다. 가장 쉬운 방법은 원소를 앞에서부터 확인하면서 일치하는지 확인하는 것이다. 리스트의 크기가 $N$일 때, $O(N)$의 시간복잡도를 가진다.

우리는 통상 코딩 테스트를 볼 때 시간복잡도를 고려하여 알고리즘을 짜야한다. 언어에 따라 다르지만, 통상 1초에 1억번 연산이 가능하다고 한다.

이때 $N$이 엄청나게 커지면 어떻게 될까? 선형탐색은 매우 비효율적일 것이다.
그래서 우리는 더 효율적인 탐색 기법이 필요하다. 이때 사용하는 것이 이진탐색이다.

이진탐색이란, 매 탐색마다 탐색 범위를 반으로 좁혀가며 빠르게 탐색하는 알고리즘이다.
하지만 이진탐색을 수행하기 위한 전제조건이 있다.

✅ 리스트(배열)가 정렬되어 있어야 한다.

이진탐색의 절차

크기가 N인 list에서 target이라는 특정 데이터를 찾아내고 싶다고 가정하자.
(left와 right는 list의 인덱스를 의미한다.)

1. left = 0, right = n - 1로 초기화한다.
2. mid = (left + right) // 2로 설정한다.
3. 만약, list[mid] == target이라면 탐색을 종료한다.
4. 만약, list[mid] != target이라면,
   • list[mid] > target : right = mid - 1로 갱신하고 2번으로 돌아간다.
   • list[mid] < target : left = mid + 1로 갱신하고 2번으로 돌아간다.

✅ mid를 설정할 때 left + (right - left) // 2로 설정하기도 한다.
(오버플로우를 피하기 위함, 단 언어에 따라 다를 수 있음?)

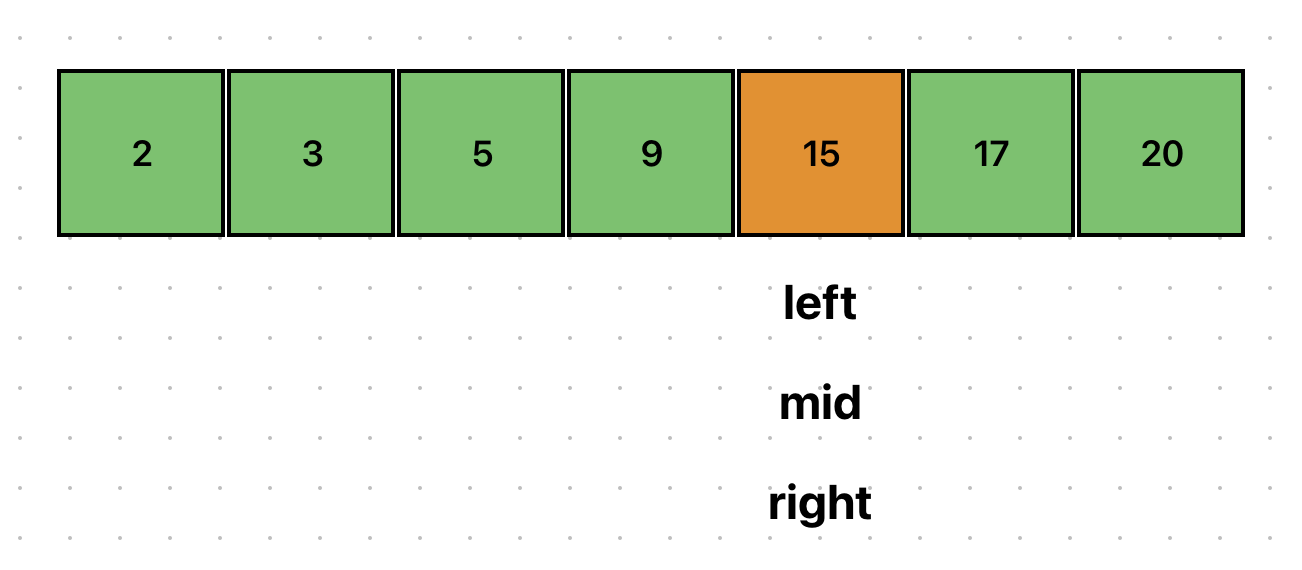
이를 그림으로 살펴보자. 아래에서 15라는 데이터를 찾고자 한다.

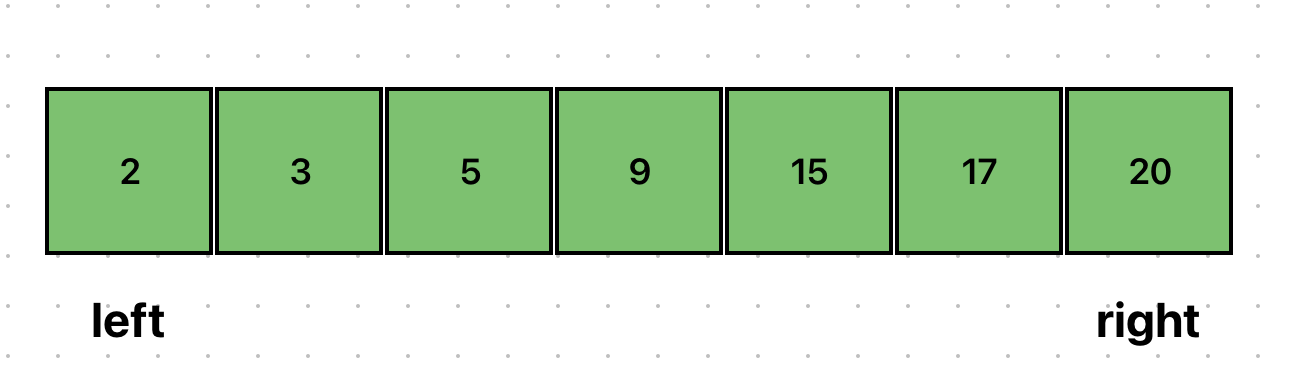
left와 right로 mid를 설정하자.
중간값이 15보다 작으므로, left를 갱신해야 한다.

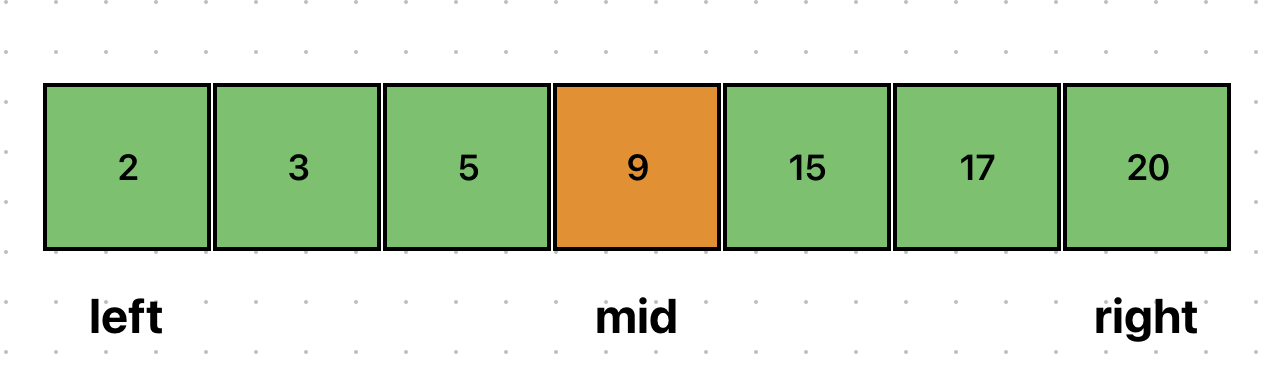
left를 갱신하고 mid를 새로 설정했다.
이번에는 중간값이 15보다 크므로, right를 갱신해야 한다.

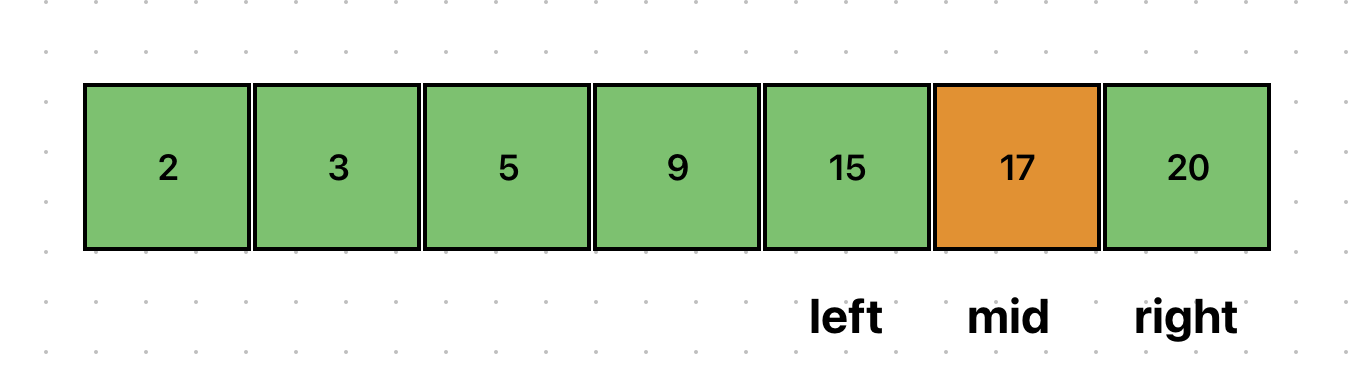
원하는 데이터 15를 찾았다.

이진탐색의 시간복잡도

이진탐색은 한번 탐색을 수행할 때 마다, 탐색의 범위가 반으로 줄어든다.
리스트의 크기를 $N$이라 하고, 반복 횟수를 k라고 한다면 다음과 같은 수식이 만들어진다.

$n*(1/2)^k = 1$
→ $n * 1/2^k$
→ $n = 2^k$
→ $k = log_2n$

따라서, 시간복잡도는 $O(logN)$이다.

이진탐색의 코드 in Python

by 재귀

def binary_search(list, target, left, right):
    if left > right:
        return None

    mid = left + (right - left) // 2
    # 찾은 경우 중간점 인덱스 변환
    if list[mid] == target:
        return mid
    # 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
    elif list[mid] > target:
        return binary_search(list, target, left, mid-1)
    # 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
    else:
        return binary_search(list, target, mid+1, right)

by 반복문

def binary_search(list, target, left, right):
	while left <= right:
    	mid = left + (right - left) // 2
        if list[mid] == target:
        	return mid
        elif list[mid] > target:
        	right = mid - 1
        else:
        	left = mid + 1
            
    return None

---

최단경로 알고리즘

최단경로 알고리즘이란, 가장 짧은 경로를 찾는 알고리즘이다.
다익스트라, 플로이드 워셜, 벨만 포드를 사용한다.

다음과 같은 문제의 종류에서 사용할 수 있다.

• 한 정점에서 다른 한 정점까지의 최단 경로
• 한 정점에서 다른 모든 정점까지의 최단 경로
• 모든 정점에서 다른 모든 정점까지의 최단 경로

다익스트라

특징

• 특정 노드에서 출발해 다른 노드로 가는 각각의 최단 경로 구하는 알고리즘
• 음의 간선이 없을 때 동작한다.
• 현실 세계는 음의 간선으로 표현되지 않아 실제 GPS 소프트웨어의 기본 알고리즘으로 채택되곤 함
• 그리디 알고리즘으로 분류되며, 매번 가장 비용이 적은 노드를 선택하는 과정을 반복함

동작 과정

1. 출발 노드 설정
2. 최단 거리 테이블 초기화
3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드 선택
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계싼해 최단 거리 테이블을 갱신
5. 위 과정에서 3, 4번 반복

그림으로 보는 동작 과정

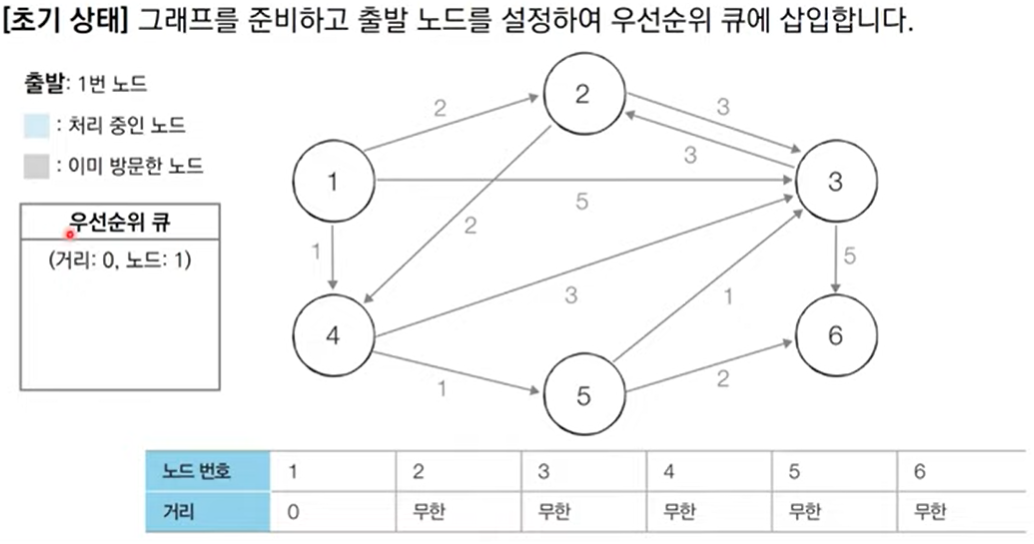
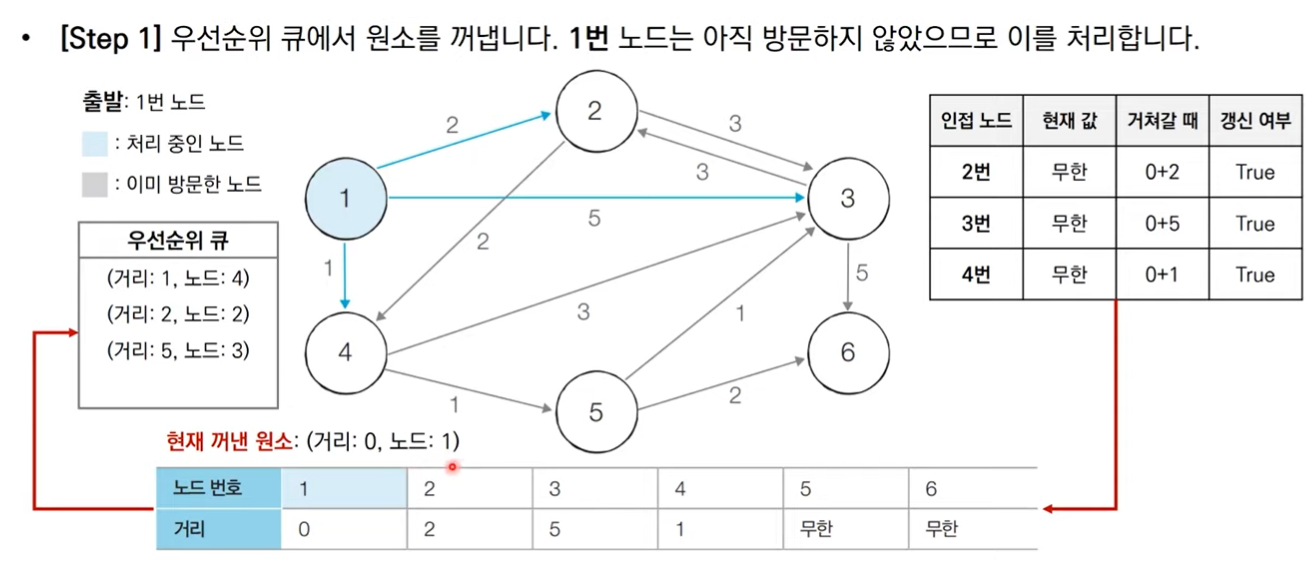
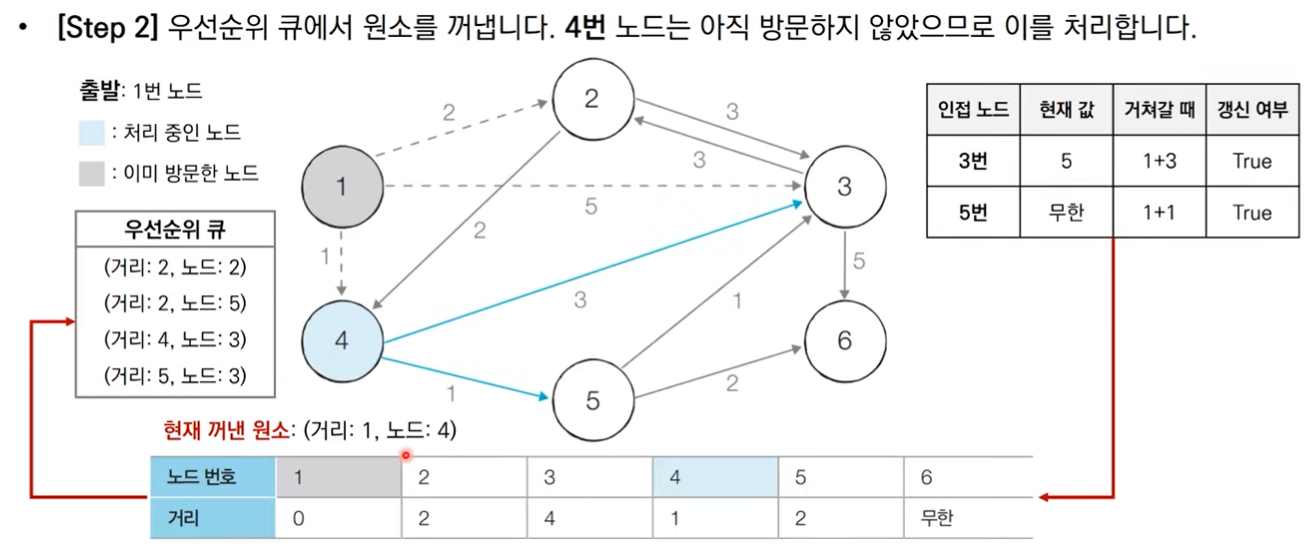
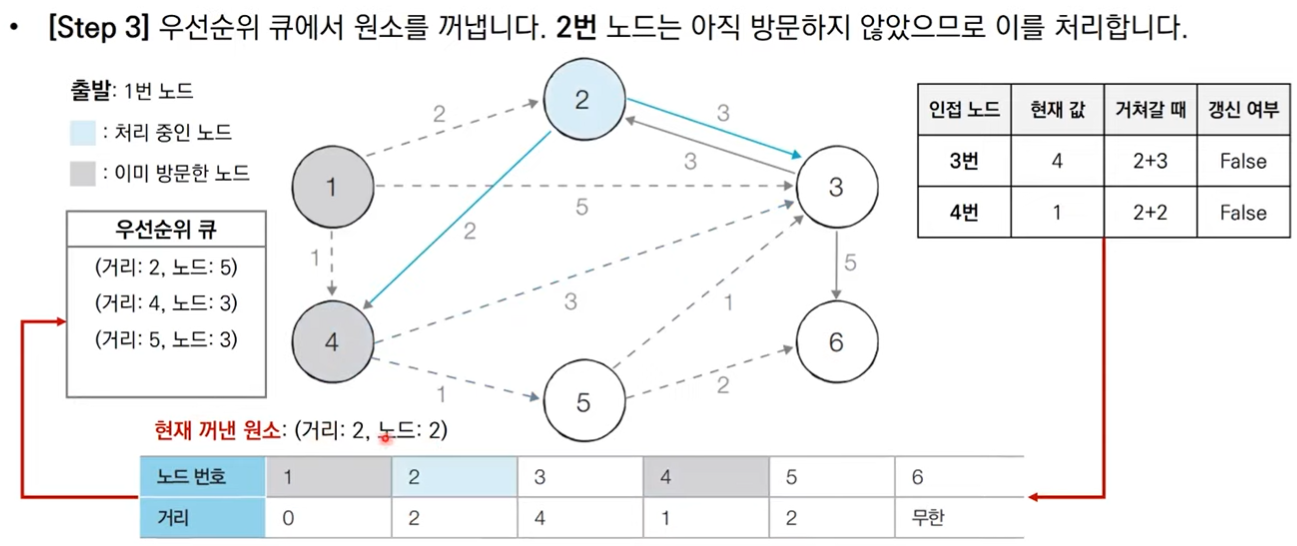
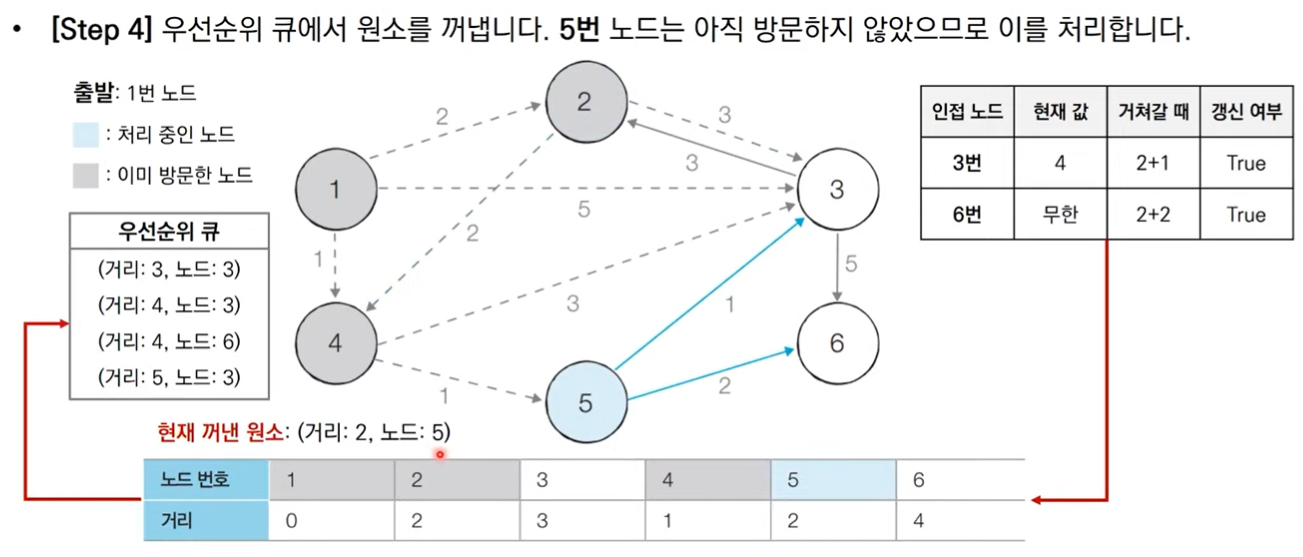
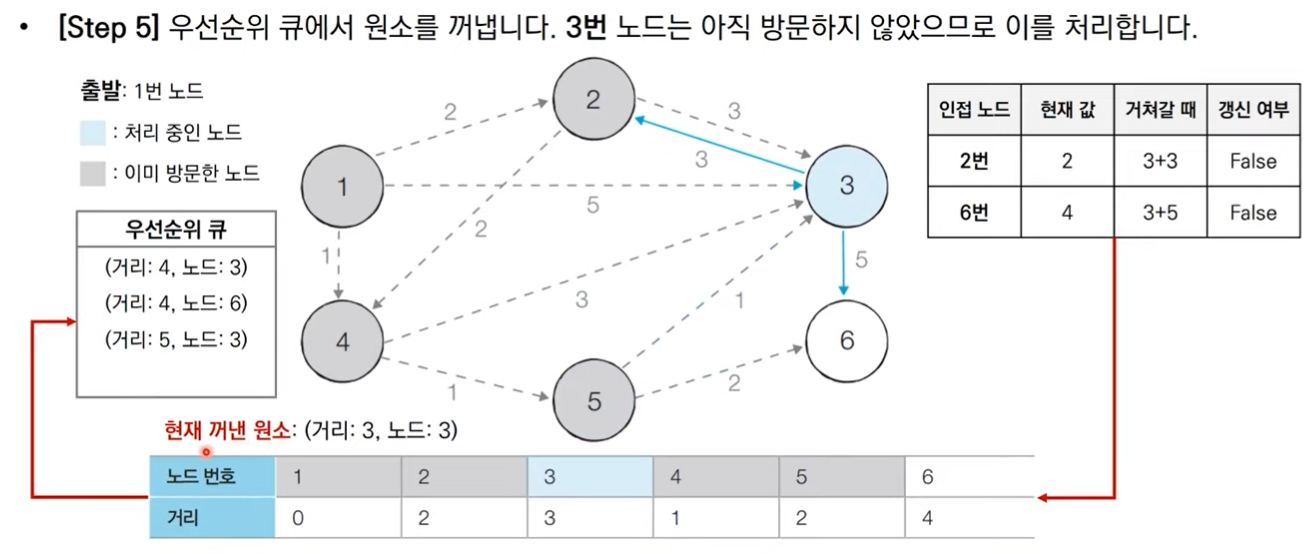
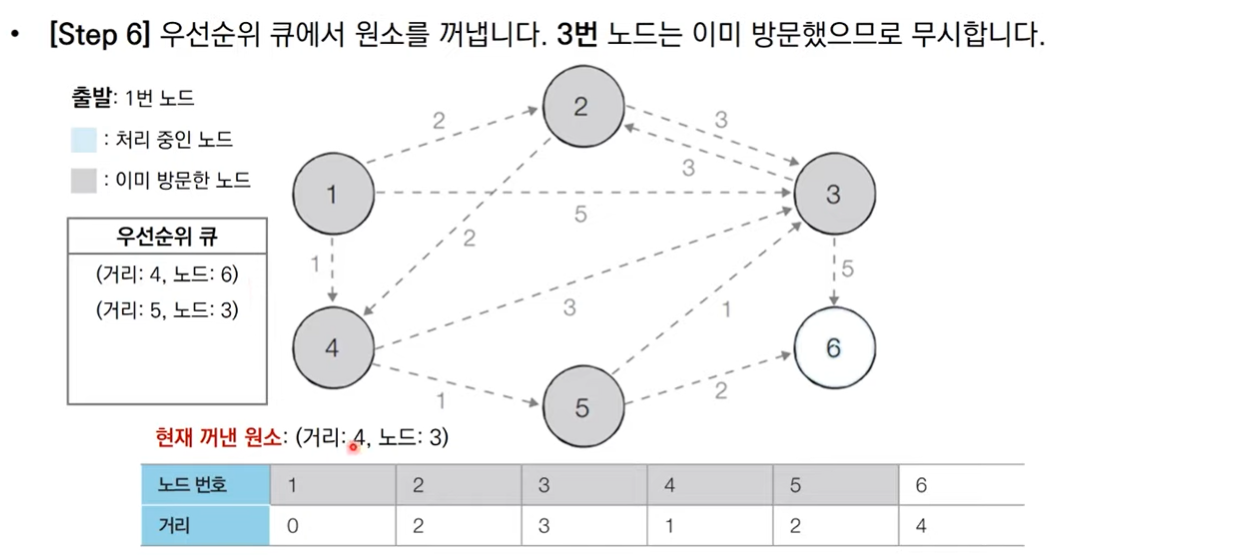
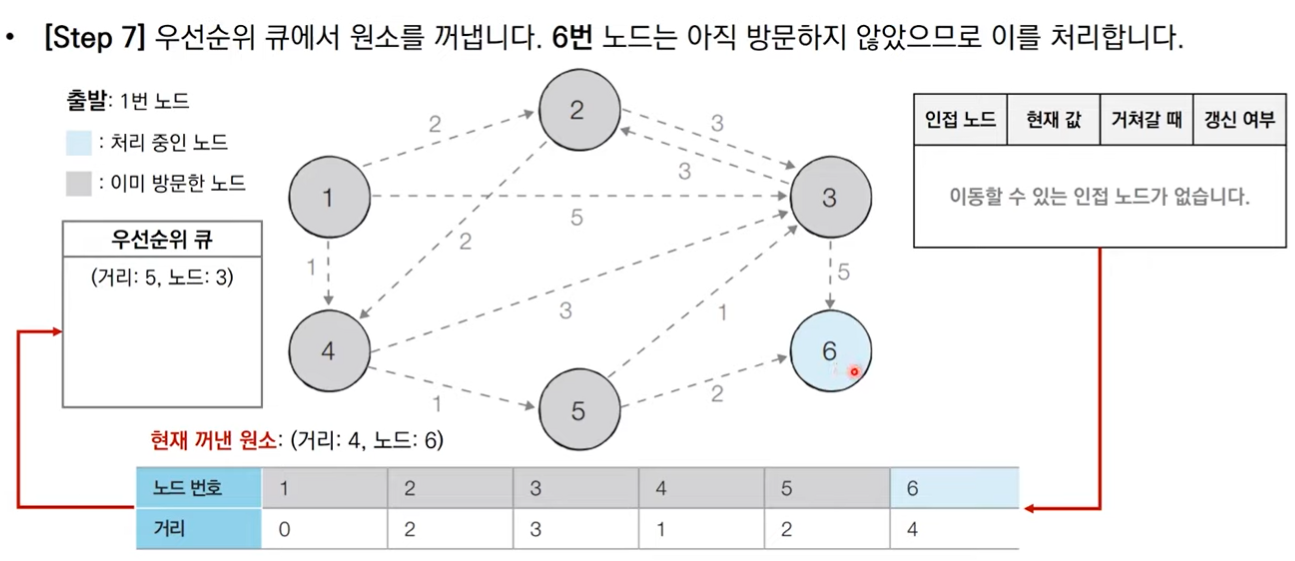
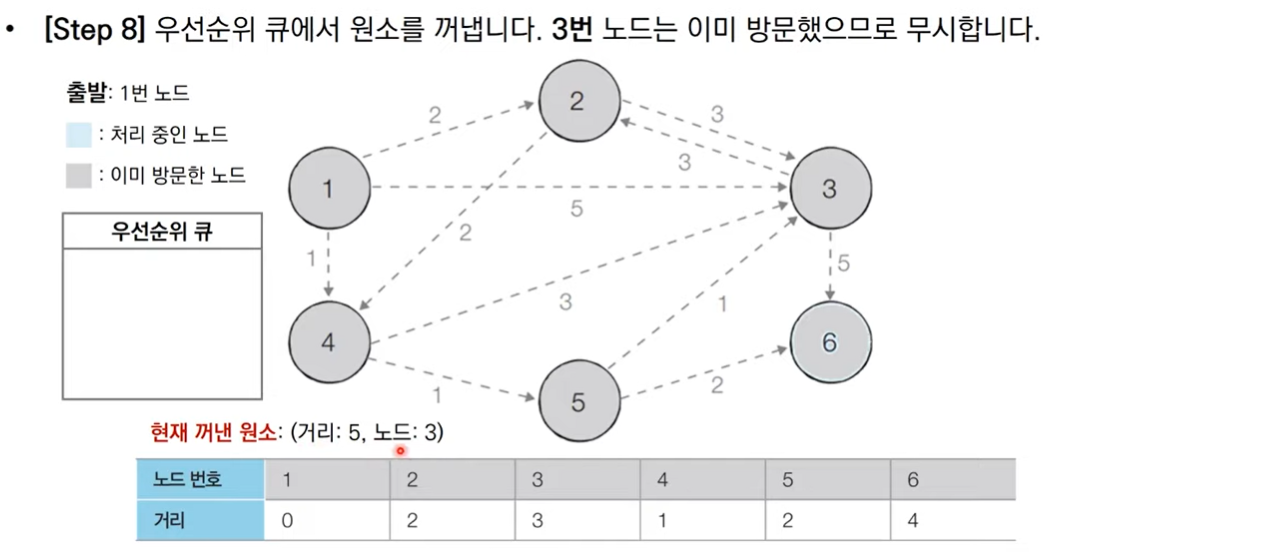
코드

import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)

n, m = map(int, input().split())	# 노드 개수, 간선 개수
start = int(input())				# 시작 노드 번호
grpah = [[] for i in range(n+1)]	# 그래프 
distance = [INF] * (n+1)			# 최단 거리 테이블

# 그래프 입력 받기
for _ in range(m):
  a, b, c = map(int, input().split())
  graph[a].append((b, c))	# a-> b 가는 비용이 c
 
def dijkstra(start):
  q = []
  # 시작 노드로 가기 위한 최단 경로는 0으로 설정한 후 큐에 삽입
  heapq.heappush(q, (0, start))
  distance[start] = 0
  while q:
    # 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
    dist, now = heapq.heapop(q)
    # 현재 노드가 이미 처리된 적 있는 노드라면 무시
    if distance[now] < dist:
      continue
    # 현재 노드와 연결된 다른 인접한 노드들 확인
    for i in graph[now]:
      cost = dist + i[1]
      # 현재 노드 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
      if cost < distance[i[0]]:
        distance[i[0]] = cost
        heapq.heappush(q, (cost, i[0]))
      
dijkstra(start) # 다익스트라 수행

시간복잡도

정점의 개수가 $V$, 간선의 개수가 $E$ 일 때,
단계마다 모든 노드를 확인하는 방식으로 구현한다면 $O(V^2)$이다.

하지만, 대부분 다익스트라를 사용할 때 힙 자료구조를 이용하여 구현한다.
이때는 $O(ElogV)$이다.

---

플로이드 워셜

특징

• 모든 정점에서 다른 모든 정점까지의 최단 경로를 구하는 알고리즘
• 2차원 테이블에 최단 거리 정보를 저장한다.
• 다이나믹 프로그래밍 유형에 속한다.
• 매 단계마다 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾는 과정이 필요하지 않다.
• 노드의 개수가 그리 크지 않을 때, 간단하게 구현할 수 있다.

동작과정

플로이드 워셜 알고리즘은 각 단계마다 특정한 노드 k를 거치는 경우를 확인한다.
즉, a → b 보다 a → k → b 가 더 짧은지 검사를 진행한다.
이를 수식으로 나타내면 다음과 같다.

$D_{ab} = min(D_{ab}, D_{ak} + D_{kb})$

그림으로 보는 동작 과정

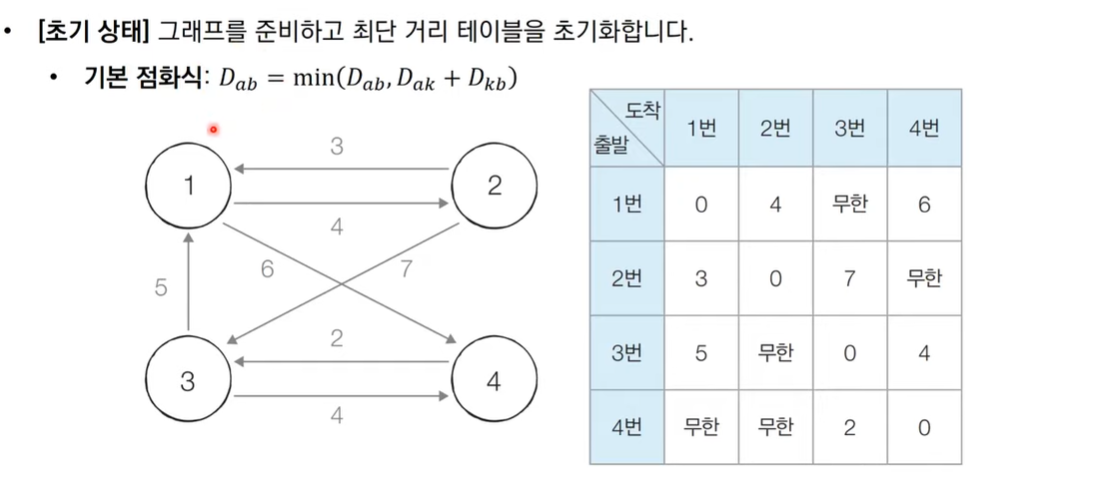
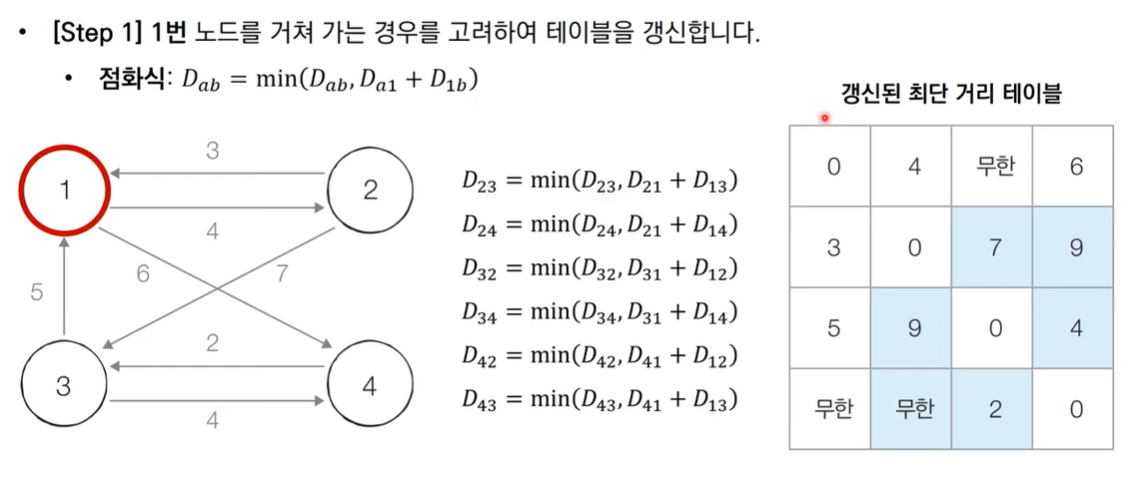
코드

INF = int(1e9)

n, m = map(int, input().split())	# 노드 개수, 간선 개수
# 그래프 초기화
graph = [[INF]* (n+1) for _ in range(n+1)]	
for a in range(1, n+1):
  for b in range(1, n+1):
    if a == b :
      graph[a][b] = 0

# 그래프 입력 받기
for _ in range(m):
  a, b, c = map(int, input().split())
  graph[a][b] = c 		# a-> b 비용은 c
  
# 점화식 따라 플로드 워셜 알고리즘 수행
for k in range(1, n+1): # 경유지
  for a in range(1, n+1): # 출발지
    for b in range(1, n+1): # 도착지
      graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])

시간복잡도

노드의 개수가 $N$개 일 때, $N$번의 단계(k 노드를 거치는 단계)를 수행한다.
각 단계마다 $O(N^2)$의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려한다.

따라서, 시간복잡도는 $O(N^3)$이다.

---

최대공약수 & 최소공배수

최대공약수는 GCD, 최소공배수는 LCM 이라고도 불리며 손코딩으로 많이 출제되는 유형이다.
최대공약수는 유클리드 호제법을 사용해서 구현할 수 있고, 최소 공배수는 최대공약수 알고리즘을 사용하여 구현할 수 있다.

최대공약수

유클리드 호제법이란,
2개의 자연수 $a$,$b$에 대해서 $a$를 $b$로 나눈 나머지를 $r$이라고 할 때 (단, $a > b$), $a$와 $b$의 최대공약수는 $b$와 $r$의 최대공약수와 같다.
이 성질에 따라, $b$를 $r$로 나눈 나머지 $r0$를 구하고 $r$을 $r0$으로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 $a$와 $b$의 최대공약수이다.

수식으로 표현하면 다음과 같다.

$GCD(A, B) = GCD(B, A\%B)$
$if A\%B = 0 → GCD = B$
$else \ \ GCD(B, A\%B)$

코드

def gcd(a, b):
    while b > 0:
        a, b = b, a % b
    return a

코드

def gcd(a, b):
    if a % b == 0:
        return b
    elif b == 0:
        return a
    else:
        return gcd(b, a % b)

최소공배수

최소공배수란, 서로 다른 수 $a$, $b$의 배수 중에서 공통되는 배수 중에 가장 작은 값을 의미한다.
$a$와 $b$의 최소공배수는 $a$와 $b$의 곱을 $a$와 $b$의 최대 공약수로 나누면 된다.

코드

def lcm(a, b):
    return a * b / gcd(a, b)

---

소수 찾기 알고리즘

일반적으로 소수 찾는 알고리즘을 하드코딩하면 다음과 같다.

def isPrime(n) {
	result = 1
    for i in range(3, n + 1):
    	check = 0
        for j in range(2, i + 1):
        	if i % j == 0 and i != j:
            	check = 0
	            break
         	elif i % j != 0:
            	check = j
     if check:
     	result += 1
        
   return result;

3부터 시작하여 소수를 판별하는 코드이다.
이 코드는 n이 $100,000$일 때 5~6초가 소요된다. 효율성이 매우 떨어지기에, 다른 코드를 생각해야 한다.

에라토스테네스의 체

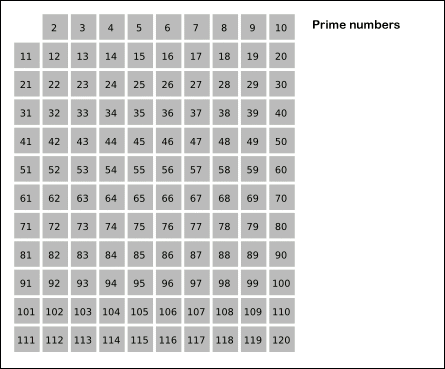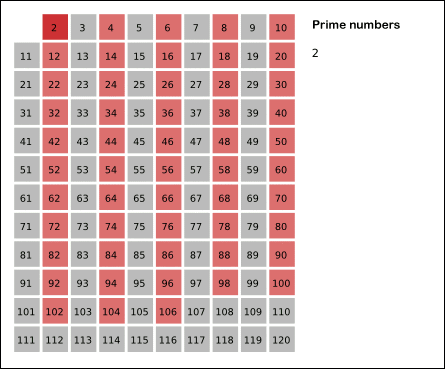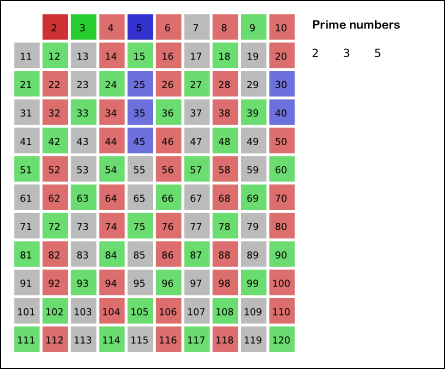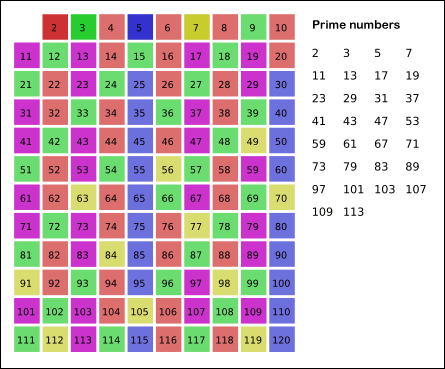
에라토스테네스의 진행방식은 다음과 같다.

1. 1을 제거
2. 지워지지 않은 수 중 제일 작은 2를 소수로 채택하고, 나머지 2의 배수를 모두 지운다.
3. 지워지지 않은 수 중 제일 작은 3을 소수로 채택하고, 나머지 3의 배수를 모두 지운다.
4. 지워지지 않은 수 중 제일 작은 5를 소수로 채택하고, 나머지 5의 배수를 모두 지운다.
5. (반복)

코드

a = [False, False] + [True] * (n-1)
primes=[]

def eratosthenes():
	for i in range(2,n+1):
    if a[i]:
      for j in range(2*i, n+1, i):
          a[j] = False

여기서 True는 소수를 의미하고, False는 소수가 아님을 의미한다.

---

재귀와 반복의 차이

재귀란 자기 자신을 계속해서 호출하는 것을 의미한다.
반복과 재귀의 차이를 살펴보자.

	반복문	재귀함수
동작	명령을 반복적으로 실행	함수 자체를 호출
체제	초기화, 조건, 루프 내 명령문 실행과 제어 변수 업데이트 포함	종료 조건(기저조건, Basis)를 지정(조건이 추가될 수 있음)
종료시점	설정한 조건에 도달 할 때까지 반복 실행	함수 호출 본문에 조건부가 포함, 재귀를 호출하지 않고 함수를 강제 반환
조건	제어 조건이 참이라면 무한 반복 발생	조건에 수렴하지 않을 경우 무한 재귀 발생
무한 반복	무한 루프는 CPU 사이클을 반복적으로 사용	무한 재귀는 스택 오버플로우 발생
스택 메모리	스택 메모리를 사용하지 않음	함수가 호출 될 때마다 새 로컬 변수와 매개 변수 집합, 함수 호출 위치를 저장하는데 사용
속도	빠른 실행	느린 실행
가독성	코드 길이가 길어지고 변수가 많아져 가독성이 떨어짐	코드 길이와 변수가 적어 가독성이 높아짐

왜 재귀를 사용하는가?

1. 재귀적인 표현이 자연스러울 때 사용한다.
   • ex. 피보나치 수열을 구할 때
2. 변수를 줄일 수 있다.
3. 가독성이 좋아진다.

재귀 사용 시 주의점

재귀함수는 stack이라는 메모리 공간을 사용한다.
반복적인 재귀 호출을 통해 stack에 자기 자신이 계속해서 쌓여가기 때문에 성능적인 측면에서 좋지 않다.

재귀함수는 stack이라는 메모리 공간을 사용하기 때문에, 무한 재귀가 발생할 경우 메모리의 제한이 있는 한 Stack Overflow가 발생하면서 프로그램이 비정상 종료된다.

---

DP와 분할정복

DP란?

• 입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서 보다 큰 크기의 부분 문제를 해결하여 최종적으로는 전체 문제를 해결하는 알고리즘
• 상향식 접근법이다.
  • 가장 최하위의 문제의 해답을 구한 후, 이를 저장하고 결과값을 활용해서 상위 문제를 해결해 나가는 방식이다.
• Memoization 기법을 사용한다.
  • 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않고 전체 실행 속도를 줄이는 기법
• 문제를 잘게 쪼갤 때, 부분 문제는 중복되어 재활용된다.
  • ex. 피보나치 수열

  	dp = [0] * n
  	dp[0] = 0
    	dp[1] = 1
    	for i in range(2, n + 1): // 2부터 시작해서 n까지 반복
    		dp[i] = dp[i-1] + dp[i-2]

분할 정복이란?

• 문제를 나눌 수 없을 때 까지 나누어서, 각각을 풀면서 다시 합병(병합)하여 해답을 얻는 알고리즘
• 하향식 접근법이다.
  • 상위의 해답을 구하기 위해 아래로 내려가면서 하위의 해답을 구하는 방식이다.
  • 일반적으로 재귀함수로 구현한다.
• 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않는다.
  • ex. 병합 정렬, 퀵 정렬 등

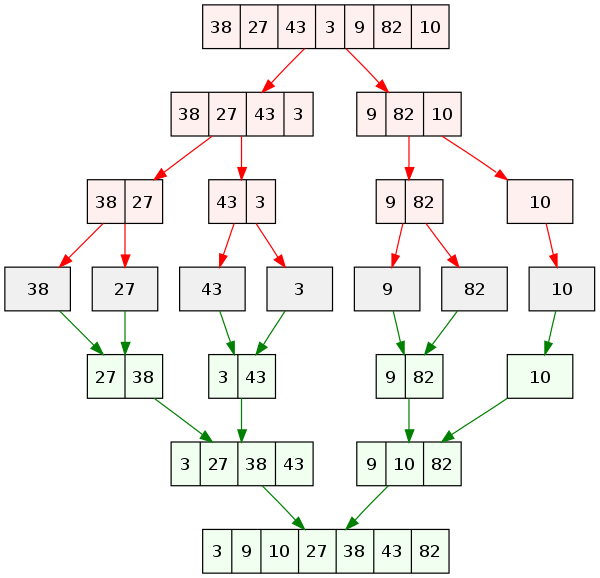
공통점과 차이점은?

공통점

• 문제를 잘게 나누어서, 가장 작은 단위로 분할하여 문제를 해결해 나간다.

차이점

• 동적 계획법(DP)
  • 부분 문제는 중복되어, 상위 문제 해결 시 재활용된다.
  • Memoization 기법을 사용한다.
• 분할정복
  • 부분 문제들은 중복되지 않는다.
  • Memoization 기법을 사용하지 않는다.

---

그리디 알고리즘

그리디(a.k.a 탐욕법) 알고리즘이란, 각 단계에서 가장 최선의 선택을 하는 알고리즘이다.

즉, 현재 상황에서 가장 좋은 결과를 선택해 나가는 방식이고 최적해를 구하는 데에 사용되는 근사적인 방법이다.

하지만, 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다.

그러나 그리디 알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이다.

그리디 알고리즘을 적용하기 위한 조건

그리디 알고리즘으로 풀 수 있는 문제는 대부분 탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이라는 두 가지 조건이 만족된다.

• 탐욕스런 선택 조건 : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
• 최적 부분 구조 조건 : 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해이다.

예시

1. 거스름돈 - 거슬러 줘야 할 동전의 최소 개수 구하기
2. 활동 선택 - N개의 활동이 있고 각 활동에는 시작 시간 및 종료 시간이 있을 때, 한 사람이 최대한 많이 할 수 있는 활동의 수를 구하기

---

백트래킹 알고리즘

백트래킹(Backtracking)이란, 해를 찾는 도중 해가 아니어서 막히게되면 그 경로를 더 이상 탐색하지 않고, 되돌아가서 다시 해를 찾아가는 기법이다.

백트래킹은 다음과 같이 설명할 수 있다.

• 모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만을 살펴보는 것이다.
• 답이 될 수 있는지 판단하고, 답이 될 수 없다면 해당 경로로는 더 이상 탐색하지 않는 가지치기를 수행한다. → 시간복잡도를 줄일 수 있다.

가지치기란?
해가 될 것 같지 않으면 멈추고 다른 경로를 탐색하는 것을 의미한다.

예시

• N-Queen
• N과 M

---

허프만(Huffman) 코딩

Huffman 코딩이란,

• 데이터 압축을 수행하는 알고리즘으로, 그리디 알고리즘에 속한다.

• 문자의 빈도 또는 확률 정보를 이용해 통계적 압축을 진행하는 기법이다.

  • 원본 데이터에서 출현 빈도가 높은 문자는 적은 비트의 코드로 변환하여 표현하고, 출현 빈도가 낮으면 많은 비트의 코드로 변환하여 표현함으로써 전체 데이터를 표현하는데 필요한 비트 수를 줄이는 방식이다.

• 고정 길이 코드와 가변 길이 코드, 두 가지 표현 방법이 존재한다.

어디에서 사용되나?

• 파일압축 in Unix
• JPEG, MP3 파일 압축을 위한 서브루틴

---

[참고&출처]
https://github.com/songhee-lee/2023-python-coding-test

https://wikidocs.net/21638

https://myjamong.tistory.com/138

https://velog.io/@kyunghwan1207/%EC%B5%9C%EB%8B%A8-%EA%B2%BD%EB%A1%9C-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

https://jina-developer.tistory.com/118

https://tecoble.techcourse.co.kr/post/2020-04-30-iteration_vs_recursion/

https://velog.io/@gillog/Algorithm-%EC%9E%AC%EA%B7%80%EC%99%80-%EB%B0%98%EB%B3%B5%EB%AC%B8

https://hanamon.kr/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%ED%83%90%EC%9A%95%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-greedy-algorithm/

https://velog.io/@junhok82/%ED%97%88%ED%94%84%EB%A7%8C-%EC%BD%94%EB%94%A9Huffman-coding