
| 출제 빈도 | 평균 점수 | 문제 세트 |
|---|---|---|
| 높음 | 낮음 | 7 / 7 |
문제
최소직사각형
코드
def solution(sizes):
w, h = -1, -1
# 명함의 가로, 세로 확인
for x, y in sizes:
if x < y: # 세로가 더 길다면
x, y = y, x # swap
w = max(w, x)
h = max(h, y)
return w * h아이디어 & 설명
문제에서 핵심은 명함을 회전시킬 수 있다는 것이다.
즉, 가로와 세로의 크기를 바꿀 수 있다.(swap)
우리는 모든 명함을 수납할 수 있는 가장 작은 지갑을 만들어야 한다.
그러므로 가로와 세로 중 임의로 기준을 설정한다.
만약, 가로를 기준으로 설정했다면 명함의 가로, 세로를 확인하면서 세로가 가로보다 더 크다면 명함을 회전시킨다.
모의고사
코드
def solution(answers):
n = 3
answer = [0, 0, 0] # 수포자 1, 2, 3이 맞힌 정답의 개수
# 수포자 1, 2, 3
give_up1 = [1,2,3,4,5]
give_up2 = [2,1,2,3,2,4,2,5]
give_up3 = [3,3,1,1,2,2,4,4,5,5]
# 채점 진행
for i, x in enumerate(answers):
if x == give_up1[i % 5]: answer[0] += 1
if x == give_up2[i % 8]: answer[1] += 1
if x == give_up3[i % 10]: answer[2] += 1
# 가장 많이 맞힌 정답 수
_max = max(answer)
# 가장 높은 점수를 받은 사람 return
return [i + 1 for i in range(n) if answer[i] == _max]아이디어 & 설명
수포자 1, 2, 3이 답을 찍는 방식은 정해져있다. 이를 일반화하면 다음과 같다.
- 1번 수포자가 찍는 방식: [1, 2, 3, 4, 5]
- 2번 수포자가 찍는 방식: [2, 1, 2, 3, 2, 4, 2, 5]
- 3번 수포자가 찍는 방식: [3, 3, 1, 1, 2, 2, 4, 4, 5, 5]
이를 통해서 정답을 맞힌 개수를 구한다. 이때 시험은 최대 개의 문제로 구성이 가능하므로, 각 문제의 인덱스를 각 수포자가 찍는 방식의 길이로 나눈 나머지를 사용한다.
만약, 문제의 수가 6개이고 1번 수포자가 정답을 맞힌 개수를 구한다고 가정하자.
문제가 [1, 2, 3, 4, 5, 5] 라면 마지막 6번째 문제는 인덱스가 5이다.
1번 수포자는 위의 일반화를 토대로, 마지막 문제를 1로 찍으므로,
1번 수포자가 찍는 방식의 인덱스는 5 % 5인 0으로 접근해야 하는것이 옳다.
이를 토대로 수포자 1, 2, 3이 맞힌 정답의 개수를 구하고, 그 중 최대로 많이 맞춘 사람의 번호를 []로 감싸 반환한다.
(문제의 조건에 맞춰 가장 높은 점수를 받은 사람이 여럿일 경우, 모두 배열에 넣어 오름차순 정렬해서 반환한다.)
소수찾기
코드
from itertools import permutations
def solution(numbers):
_list = list(numbers) # 리스트로 변환
nPr = set() # 만들 수 있는 수
# 소수 판별 알고리즘
def isPrime(n):
# 0과 1은 소수가 아님
if n < 2: return False
# 제곱근까지 범위를 줄여서 소수 판별
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return False
return True
for n in range(1, len(_list) + 1):
perm = permutations(_list, n) # 순열 구하기
for item in perm:
nPr.add(int(''.join(item))) # 조각 붙이기
count = 0 # 소수 개수
for item in nPr:
if isPrime(item): count += 1
return count아이디어 & 설명
먼저, numbers를 구성하는 수들을 list에 저장하고 순열을 구한다.
순열안에는 각 수들의 조각이 따로 존재하므로, 이를 붙여서 저장한다.
단, 이때 중복하는 수가 나올 수 있으므로, set에 저장한다.
(예시에서 [0, 1, 1]일 때 1이 2개이므로 11이 2번 나올 수 있다. 이는 같은 수이므로 하나로 카운트해야 한다. 따라서, set에 저장한다.)
모든 순열을 구하고 저장했다면, 하나씩 소수인지 판별한다.
카펫
코드
def solution(brown, yellow):
answer = []
for x in range(3, brown): # 세로
for y in range(3, brown): # 가로
a = (x - 2) * (y - 2) # 노란칸
b = x * y - a # 갈색칸(전체에서 노란칸을 뺀 나머지)
# 주어진 인자와 같다면
if a == yellow and b == brown:
return [y, x]
return answer아이디어 & 설명
문제의 조건에서 카펫의 정중앙은 노란색으로 칠해진다.
정중앙이 존재하려면 적어도 카펫의 크기는 부터 시작한다.
따라서 x = 3, y = 3부터 시작해서,
노란칸과 갈색칸이 인자로 주어진 yellow와 brown과 같다면 현재 가로(y)와 세로(x)를 배열에 담아 반환한다.
(이때 가로가 세로보다 크거나 같다는 조건이 있기 때문에 y를 가로, x를 세로로 설정해야 한다. → for문의 순서에 따라 달라진다.)
피로도
코드
answer = -1 # 최대 던전 수
def solution(k, dungeons):
check = [0] * len(dungeons) # 던전 방문처리 리스트
# DFS
def dfs(fatigue, count):
global answer
for i in range(len(dungeons)):
need, consume = dungeons[i] # 최소 필요 피로도, 소모 피로도
if fatigue >= need and not check[i]: # 남은 피로도가 더 많고, 방문하지 않은 던전이라면
check[i] = 1 # 방문처리
dfs(fatigue - consume, count + 1) # 재귀
check[i] = 0 # 방문해제
answer = max(answer, count) # 탐험할수 있는 최대 던전 수 갱신
dfs(k, 0) # DFS 수행
return answer아이디어 & 설명
던전은 순서와 상관없이 방문할 수 있다. 예를 들어 3개의 던전이라면,
- 1 - 2 - 3
- 1 - 3 - 2
- 3 - 1 - 2 ...
그리고 던전의 개수는 1이상 8이하이다. for문을 8개 써도 가능하지만 이는 비효율적이다.
따라서, 우리는 DFS를 떠올렸어야 한다.
(fatigue : 남은 피로도, count : 던전 탐험 횟수)
모든 던전을 순회하면서, 현재 던전이 필요로 하는 피로도(최소 필요 피로도)보다 남은 피로도가 크거나 같고, 현재 던전을 방문한적이 없다면 방문처리를 해주고 dfs를 재귀호출한다.
이때 남은 피로도를 의미하는 fatigue에서 소모한 피로도를 빼고 탐험 횟수를 1 증가시키고 호출해야 한다.(dfs(fatigue - consume, count + 1))
전력망을 둘로 나누기
코드
from collections import deque
def solution(n, wires):
graph = [[] for _ in range(n + 1)] # 전력망 연결 정보
# 연결 정보 초기화
for v1, v2 in wires:
graph[v1].append(v2)
graph[v2].append(v1)
# BFS - v1에서 시작
def bfs(v1, v2):
q = deque([v1])
check = [0] * (n + 1) # 방문 처리 리스트
check[v1] = 1
cnt = 0
while q:
cur = q.popleft()
cnt += 1 # 송전탑 개수 + 1
for nxt in graph[cur]:
# v2는 끊어져있다고 가정해야 하고
# 다음 노드는 방문하지 않았어야 한다.
if nxt != v2 and not check[nxt]:
q.append(nxt)
check[nxt] = 1
return cnt
# 두 전력망의 각 송전탑 개수가 가능한 비슷하도록
# 즉, 송전탑 개수들의 차이(절댓값)를 저장
_abs = n
for v1, v2 in wires:
# v1에서 시작했을 때 송전탑 개수
# v2에서 시작했을 때 송전탑 개수
count1, count2 = bfs(v1, v2), bfs(v2, v1)
_abs = min(_abs, abs(count1 - count2)) # 더 작은 값으로 갱신
return _abs아이디어 & 설명
문제는 간단하다.
특정 두 전력망 사이의 연결을 끊었을 때 만들어지는 두 전력망을 이루는 송전탑의 개수의 차이(절댓값)의 최소값을 구해야 한다.
연결을 끊었을 때 그림을 자세히 살펴보면, 무언가 떠오른다.
0과 1로 이루어져있는 격자 칸에서, 1로 연결되어있는 칸(상,하,좌,우로 연결되어있는)의 개수를 구하는 문제와 비슷해보인다.(백준 단지번호붙이기)
이는 BFS로 풀 수 있다.
wires에서 연결 정보를 하나 꺼낸다. v1과 v2로 이루어져있는데 이를 인자로 bfs를 호출한다 → bfs(v1, v2)
이 의미는 v1에서 시작하고 연결된 송전탑을 탐색하되 v2는 포함하지 말라는 것이다.
즉, v2를 만나면 종료하는 것과 비슷한 맥락이다.
그림으로 살펴보자. v1 = 7, v2 = 4이라고 가정하자.
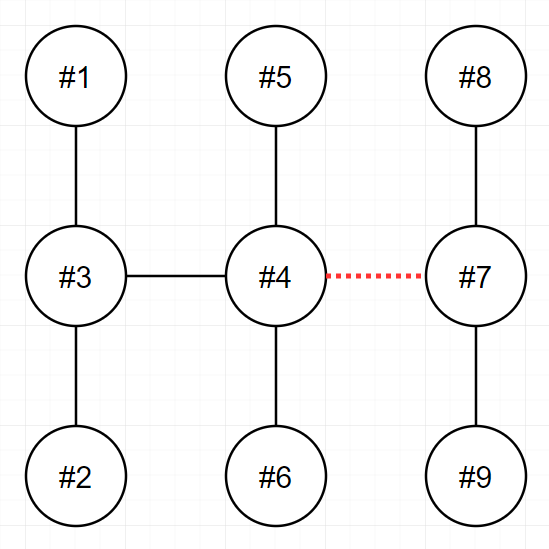
7에 연결된 송전탑은 4, 8, 9이다.
차례대로 탐색한다고 가정하면,
- 4를 만났다 : 4는
v2이므로 큐에 넣지 않는다. (즉, 카운트하지 않는다.) - 8을 만났다 : 8은 v2가 아니므로 큐에 넣는다.
- 9를 만났다 : 9는 v2가 아니므로 큐에 넣는다.
모든 탐색을 끝마치면, 총 2개(8, 9)가 큐에 존재한다.
8과 9는 연결된 송전탑이 더 이상 없으므로 while문이 종료된다.
이때 cnt 즉, 총 송전탑의 개수는 3개이다.(처음 송전탑 7번(v1)을 탐색할 때 카운트도 포함된다.)
위의 과정을 모든 연결정보에 대하여,
bfs(v1, v2), bfs(v2, v1)을 수행해서 절댓값(차이)의 최솟값을 구한다.
모음사전
코드
def solution(word):
answer = 0
vowel = 'AEIOU' # 알파벳 모음
word_list = [] # 만들 수 있는 길이 5 이하의 모든 단어
# DFS
def dfs(cnt, w):
if cnt == 5: # 길이가 5라면 종료
return
# 단어 만들기
for i in range(len(vowel)):
word_list.append(w + vowel[i]) # 단어 수록
dfs(cnt + 1, w + vowel[i]) # 재귀 호출
dfs(0, "") # DFS 호출
# word_list는 0-index 기반이므로 1을 더해서 반환한다.
return word_list.index(word) + 1아이디어 & 설명
길이 5 이하인 모든 단어를 만들기 위해 DFS를 사용했다.
일단, 하나의 알파벳마다 5개의 경우의 수가 존재하고 길이는 최대 5이므로, 시간복잡도를 계산해봤을 때 로 충분히 가능하다고 판단했다.
(시간 복잡도 틀릴 수 있음)
단어는 다음의 순서로 만들어지며 list에 저장된다.
list는 0-index 기반이므로,
최종적으로는 list에서 word의 인덱스를 찾고 1을 더한 값을 반환한다.
