이미지 변환에는 여러가지가 있다
대표적으로는 확대, 축소, 회전 등이 있다. 이런 변환들 중에서 점, 직선, 평면을 보존하는 선형 매핑을 Affine변환이라고 한다. 즉, 아핀 변환 후에도 평행한 선들이 그대로 평행하게 유지된다.
여기서는 shear, scaling, rotation만 볼 것이다.
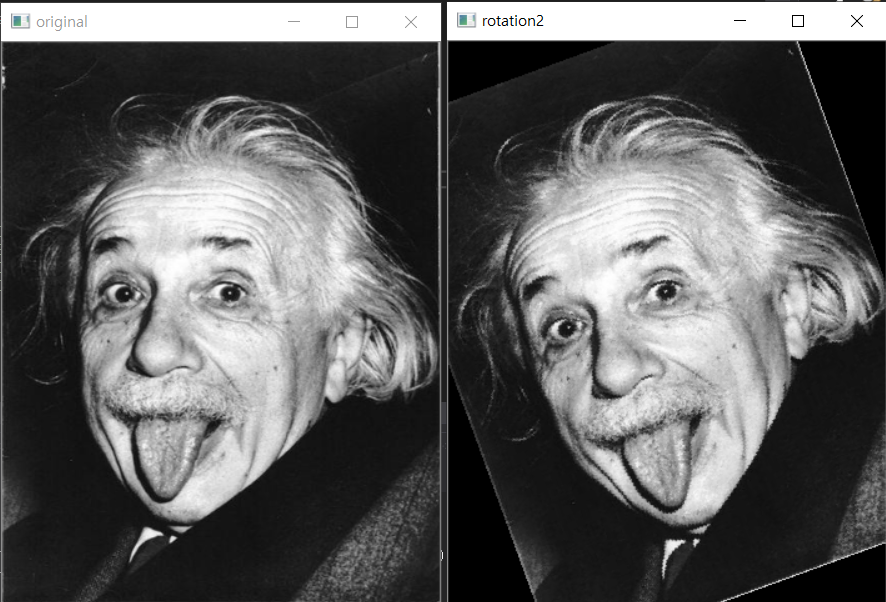
모두 역방향 매핑을 사용했다.
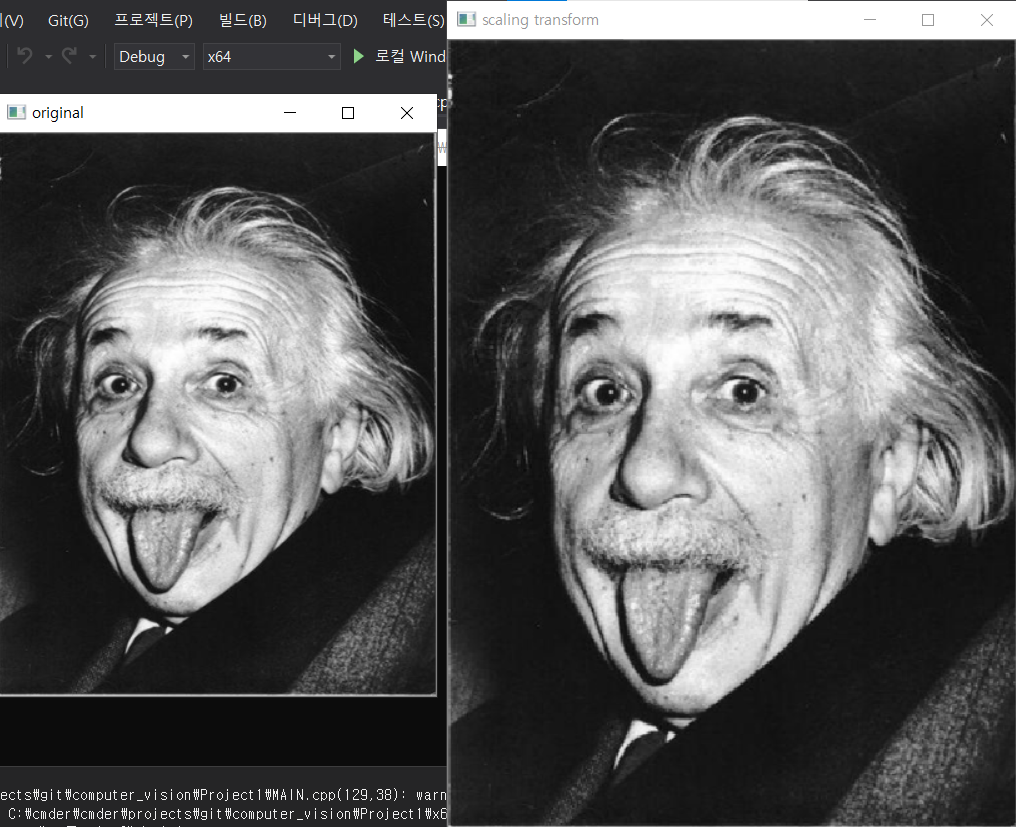
- scaling
확대, 축소를 말한다. x축으로 a배, y축으로 b배
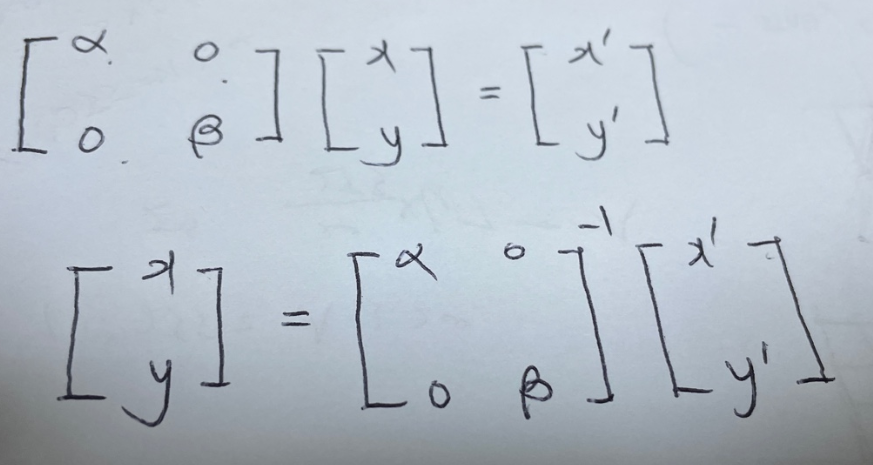
선형대수학 중 행렬곱을 안다면 위처럼 나온다는 것을 단번에 알 수 있다.
다만 역방향 사상이므로 역행렬을 곱해 목적지인 x', y'를 기준으로 x, y를 구하는 것이다.
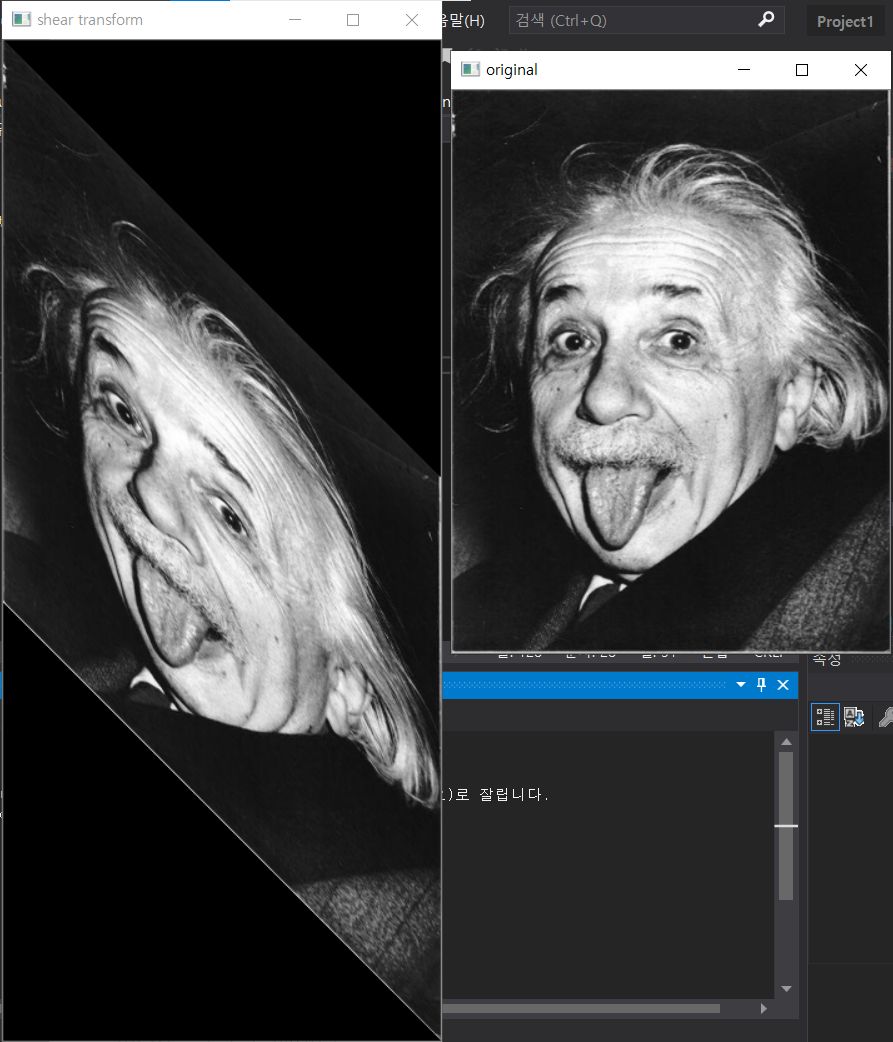
- shear
shear 연산의 예이다.
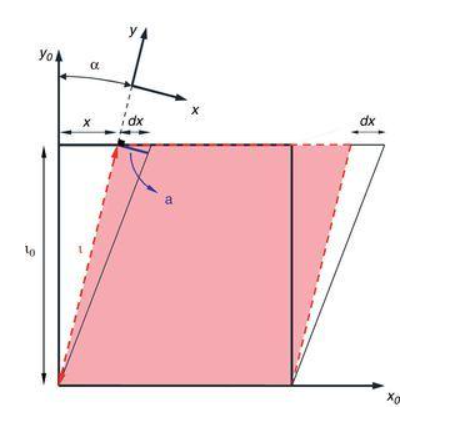
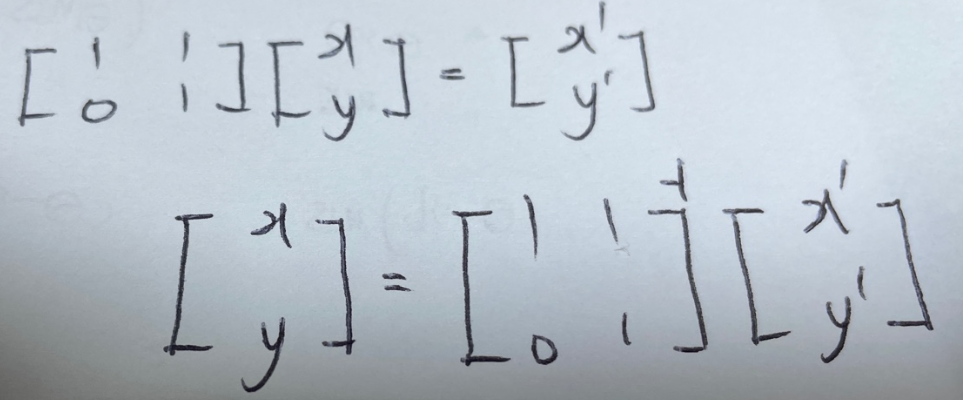
이 거는 x축은 그대로 두고 y축만 기울이는 것을 예시로 들었다 반대로 x축을 기울일 수도 있다. 다만 x축과 y축의 목적지가 같으면 안된다. scaling에서 설명한 것처럼 동일하게 역행렬을 구해 곱해준다.
-rotation
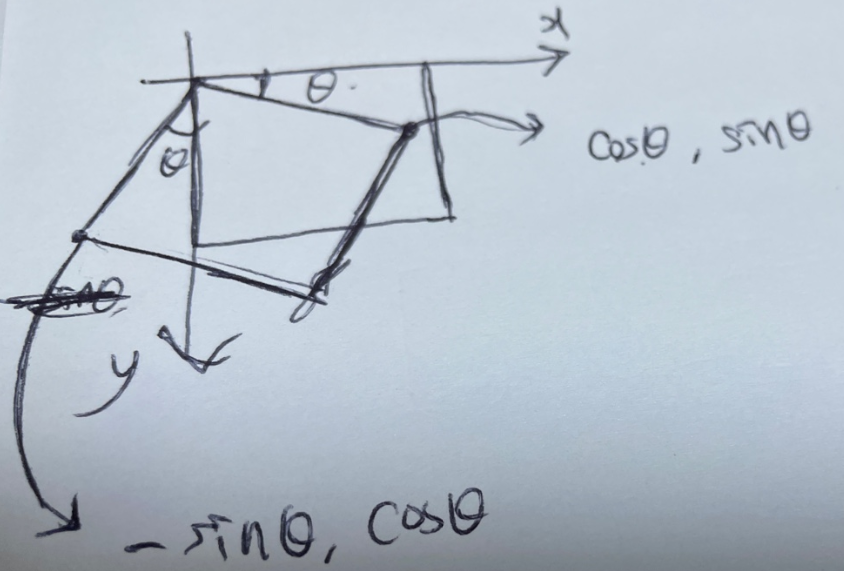
위의 이미지처럼 생각해본다면 아래의 이미지처럼 변환행렬을 쉽게 구할 수 있다.
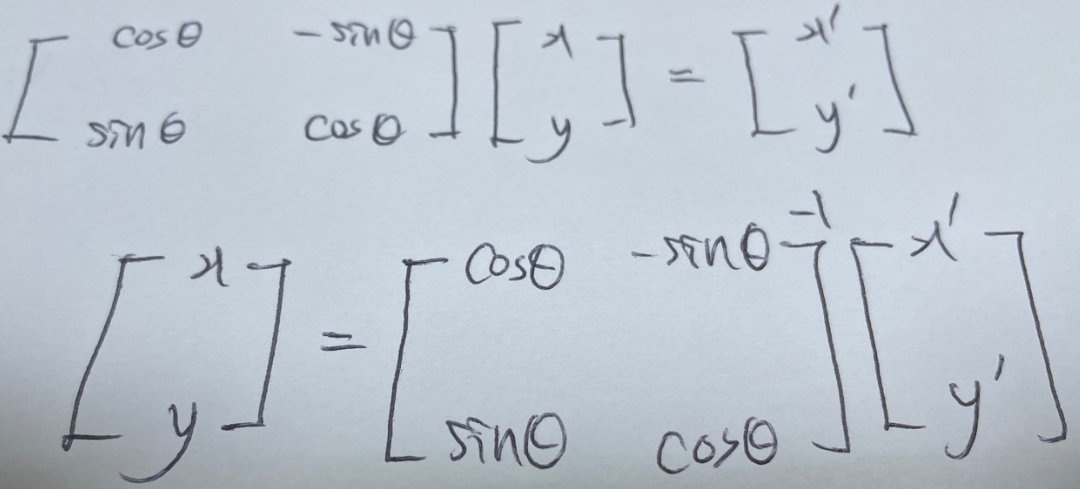
그런데 여기서 문제가 하나 발생한다. 보통 이미지 회전을 생각하면 원점기준이 아닌 이미지의 중앙을 기준으로 회전하는 것을 생각하기 때문이다. 그런데 위의 식은 원점기준으로 회전을 한다.
그러면 이미지의 중점을 원점으로 이동시키면 해결이 된다.
즉, 이미지의 중점을 원점으로 이동시킨 뒤 회전변환을 하고 다시 이미지의 중점을 원위치로 돌리면 된다. cx, cy를 이미지의 중앙이라고 할 때 아래의 사진처럼 다시 구할 수 있다.
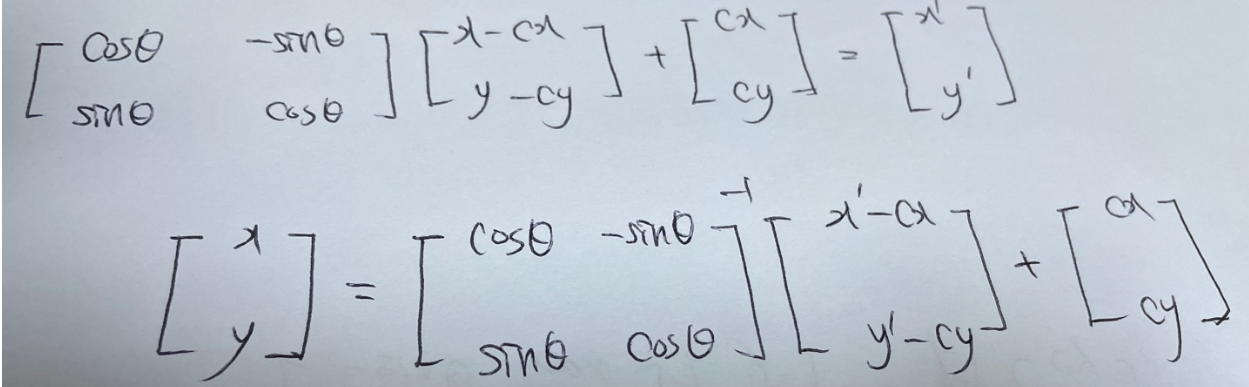
OpenCV 1

OpenCV 2

직접 구현

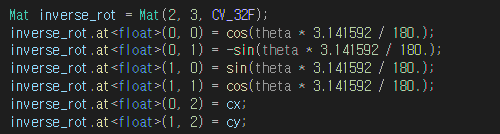
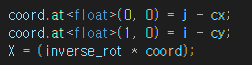
여기서는 회전변환의 행렬을 3X3으로 구성해 뒤의 cx, cy를 더해주는 부분을 하나의 행렬로 묶어버린 것이다. 그러면 좌표도 2X1에서 3X1로 만들어 [x, y, 1]^T의 형태로 만들어 한 번의 행렬곱으로 계산을 끝낼 수 있다.
그래서 Affine변환은 최종 변환 행렬을 일반화 시킨다면
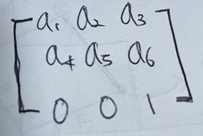
자유도가 6인 이런 행렬이 된다. shear와 scaling은 a3, a6가 0이 된다.
자유도가 6이므로 Affine변환은 3개의 좌표만 있다면 a1 ~ a6를 다 찾을 수 있다.
