Perspective 변환

지난 글에서 affine transformation을 다뤘다.
회전, 이동, shear 변환들로 총 자유도가 6인 행렬을 곱해 구할 수 있었다.
하지만, affine 변환은 평행한 선들이 유지된 채로 변환이 되는 것이었는데 평행이 유지되지 않은 채 변환되는 것은 어떻게 될까 그 중에서도 원근감을 나타내는 원근 변환을 알아보자/

우선 회전변환에서 차원을 하나 추가해 좌표를 [x, y, 1]^T의 형태로 나타내주는 것에서 시작이다. 실제 이미지는 3차원 공간에 있는 물체를 2차원의 이미지 평면에 투영하는 것이라고 볼 수 있다. 이 투영은 원근투영이 되고, 투영의 중심이 바로 관측점이 된다.

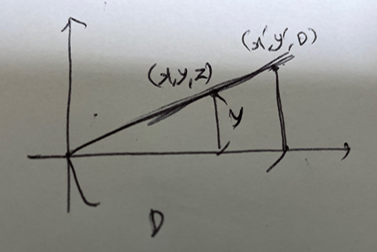
그 모습을 옆에서 봤다고 가정하면 위에 그림처럼 나타낼 수 있다.
그러면 삼각형의 닮음을 이용하여
$y'/y = D/z, x'/x = D/z$ 가 된다.
z로 나누어주는 것은 perspective divide라고 한다. 멀리 있음에 따라 z값이 커지고 투영면에서는 원점과의 거리가 가까워진다.

그런데 우리는 앞서 z를 1로 두고 했으므로 $y = y'/D, x = x'/D$가 된다.

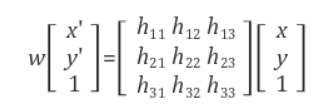
그래서 해당 좌표계에서 위의 사진처럼 어떠한 변환을 가한다면 다른 카메라 위치에서 찍은 거처럼 표현할 수 있다. affine변환과는 다르게 원근을 표현하기 위해 z축을 조정한다고 생각해 변환행렬의 변수가 늘었다.
위의 그림처럼 자유도가 8과 같다.(위위 사진처럼 보정만 해준다면 D나 W가 어떤 값을 가져도 상관이 없기 때문에 자유도가 8이다.)

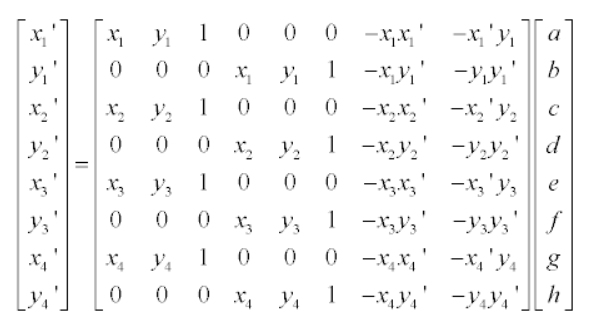
8개의 변수를 찾기 위해 4개의 좌표가 필요하다. (좌표 1개당 x, y를 가지므로)
4개의 좌표가 있다면 perspective 변환을 할 수 있는 것이다. 그 변수를 구하기 위해 위처럼 행렬화를 통해 푼다.

이것으로 2차원 평면에서 임의의 사각형을 임의의 사각형으로 매핑할 수 있다.
가장 많이 사용되는 것이 기울어지게 찍은 사진들을 다시 정면에서 찍은 거처럼 바꿀 때 사용되는 것 같다.

변환 후 도착지점 선택

변수 8개를 찾기 위한 행렬화

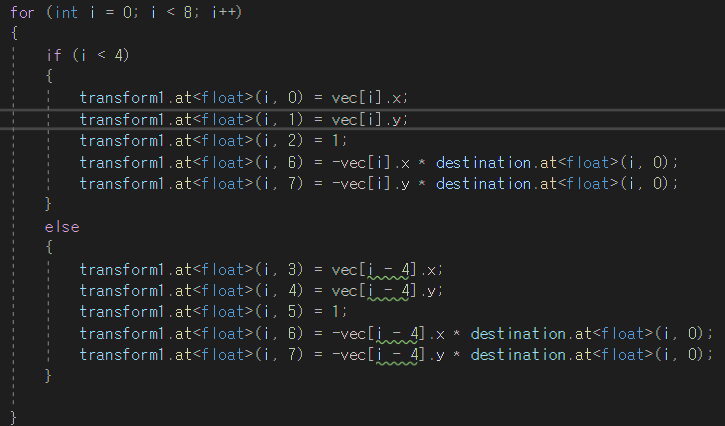
찾은 변수 8개를 행렬화 시킨뒤 (역방향 사상을 위해 역행렬)

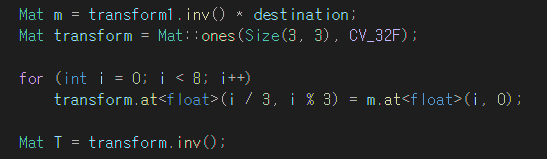
좌표 계산

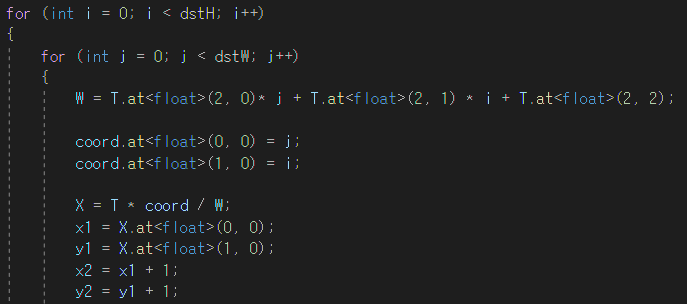
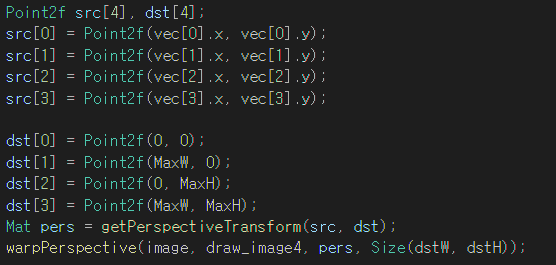
opencv의 getPerspectiveTransform을 이용한 코드

결과

이번 perspective 변환은 개념적으로 굉장히 어려웠는데 이해한 대로 작성해보았다.
이것으로 고비를 한 번 넘겼다고 본다.
위의 결과를 보면 getPerspectvieTransform을 이용하지 않고 직접 좌표계산한 것을 보면
이미지가 약간 깨지는 계단 현상이 보인다. 다음은 이 것을 보완하기 위한 보간법을 알아보도록 하자

참고 링크 : https://b.mytears.org/2007/10/599/, https://darkpgmr.tistory.com/79