Nesterov Momentum

keras의 SGD optimizer를 사용하던 중 nesterov라는 옵션이 궁금해졌다.

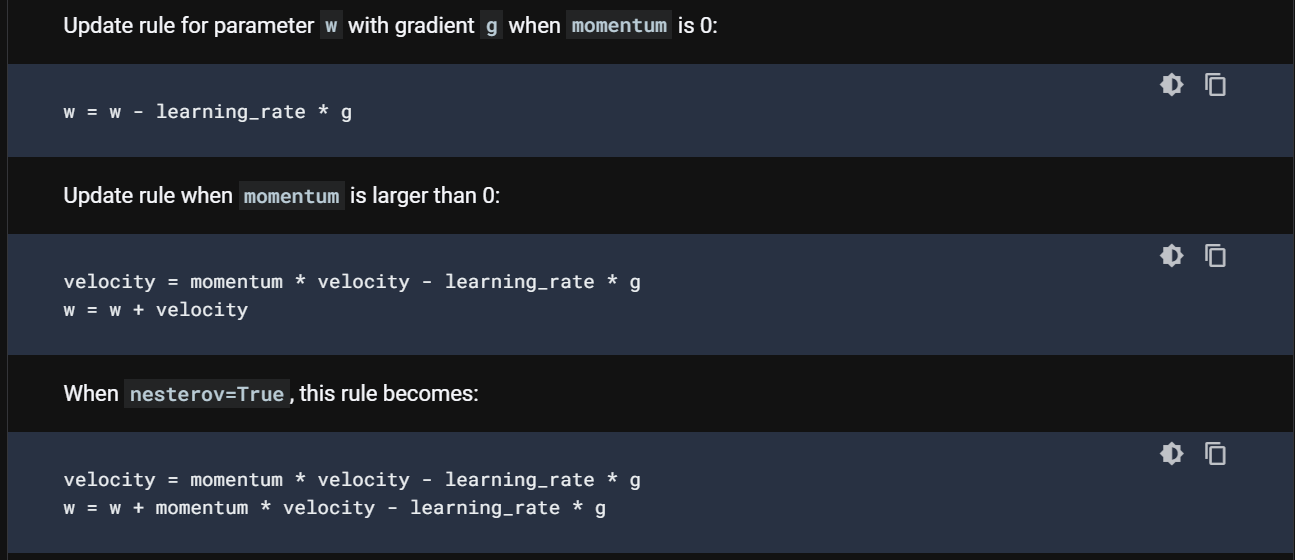
tensorflow 공식 홈페이지에 들어가 확인했더니 아래를 보니 설명이 나와있었고 기존의 SGD와 momentum은 다뤄봤던 터라 이해하는데 어렵지 않았다.
하지만 nesterov 코드를 봤는데, 원리가 무엇인지 저것만 보고선 알 수가 없어 구글링을 해봤다.

내용을 한 번 정리해보자면, 우선 momentum은 현재 그레디언트에 과거에 누적했던 그레디언트를 어느정도 보정해
과거의 방향을 어느정도 반영하는 것으로 볼 수 있다.

$v_{t+1} = \mu v_t - lr \nabla_W Cost(W)$
$W_{t+1} = W_t + v_{t+1}$
로 나타낼 수 있다.

그럼 네스테로프 모멘텀의 공식을 보면
$v_{t+1}=\mu v_t - lr \nabla_WCost(W + \mu v_t)$
$W_{t+1} = W_t + v_{t+1}$

공식이 매우 비슷하게 생겼지만 그레디언트를 구할 때 현재 위치에서 $\mu v_t$만큼 이동한 후 그레디언트를 구한다.
이를 먼저 모험적으로 진행한 후 에러를 교정한다고 표현한다고 한다.

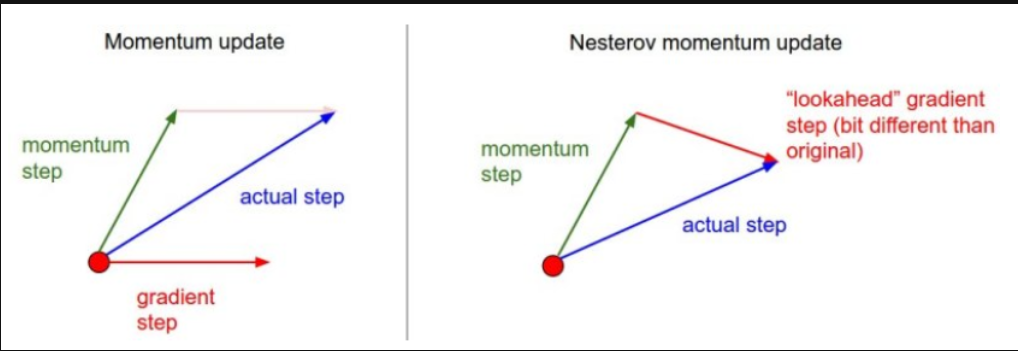
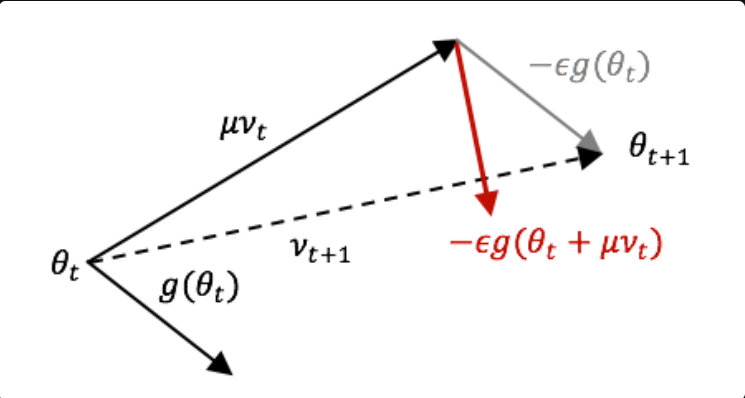
그래서 구글링을 한다면 위와 같은 이미지를 많이 볼 수 있다.
이 것을 여러 스텝으로 진행한 이미지를 보면

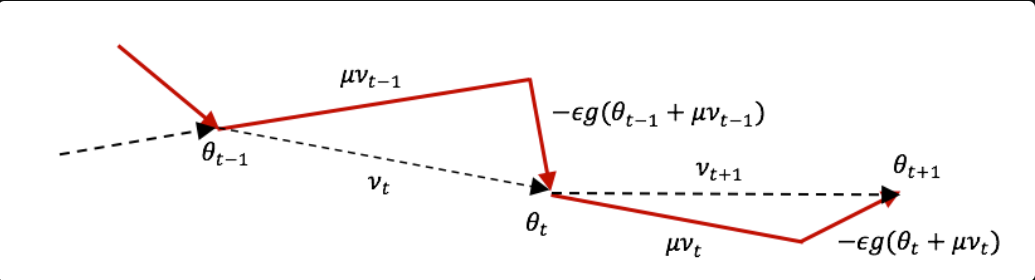
와 같이 나온다.
근데 이 것만 봤을 때 그레디언트를 구할 때에 현재 위치에서 $\mu v_t$만큼 이동한 후에 그레디언트를 구하게 된다면 뭔가 복잡해보이는 느낌과 어떻게 해야되지라는 생각이 먼저 들었는데 천재들이 이미 다 방법을 알아놨다.

약간의 트릭을 이용한다.

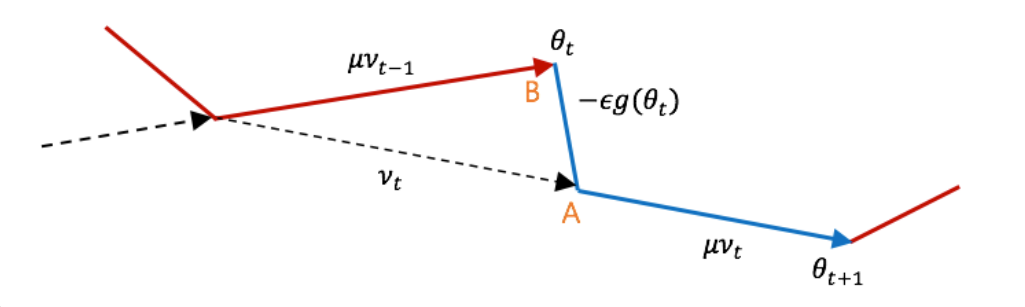
위의 이미지에서 $\theta_t$의 위치만 조정한다면 쉽게 나타낼 수 있게 된다.
위 이미지에서 $\mu v_{t+1} = \mu v_t - \epsilon \theta_{t+1}$로 쉽게 구할 수 있기 때문에 t 자리에 t-1을 넣어준다면 $\mu v_t$를 쉽게 구할 수 있다.

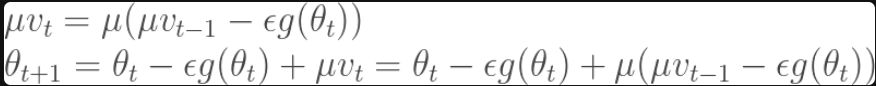최종으로 위와 같은 식을 얻을 수 있게 된다.
그럼 맨 위에서 봤던 tensorflow 공식 페이지에 나와있는 코드와 동일하다는 것을 확인할 수 있다.

이 트릭은 위 그림처럼 완전히 동일하지는 않지만 네스테로프 모멘텀의 경로를 그대로 따르고 있으므로 학습을 많이 반복하게 된다면 최적점에 수렴하여 전체 파라미터 공간에서 거의 동일하게 될 것이기 때문에 가능하다고 나와있다.

아래에 남긴 출처를 보면 내용이 명확하게 잘 정리되어 있다.

출처 : https://tensorflow.blog/2017/03/22/momentum-nesterov-momentum/, https://www.tensorflow.org/api_docs/python/tf/keras/optimizers/SGD