중요할 것 같지 않게 느껴지지만 초기 가중치 설정은 매우 중요하다.
초기 가중치를 잘못 설정한다면 local minimum에 수렴할 가능성이 커지거나
gradient vanishing / exploding 혹은 학습이 제대로 이루어지지 않을 수도 있다.
-
0으로 초기화시
만약 초기값을 모두 0으로 설정한다면 모든 뉴런이 동일한 출력값을 내어 모두
동일한 그레디언트를 가지게 된다. 뉴런이 한 개인 거 처럼 동작되어 학습이 제대로 이루어 지지 않는다. -
activation function을 sigmoid
activation function으로 sigmoid를 사용할 때에는 weight의 절대값이 큰 상태로 초기화가 된다면,
gradient vanishing 문제가 일어난다.
만약, 이전 hidden layer에서 sigmoid를 거쳐오면 0~1사이의 값이 나오고 weight값이 평균이 0이고 표준편차가 1인 상태로 초기화되어 곱셈과 덧셈연산이 일어났다고 가정하자
그러면 뉴런의 수가 N이라고 하면 N ~ -N의 범위로 나오는데 아래의 그림처럼 4 or -4만 나와도 기울기가 이미 거의 소실되어버렸다.
- activation function을 relu
마찬가지로 weight의 절대값이 크면 0으로 가거나 gradient exploding이 일어난다.
sigmoid를 예시로 했을 때 뉴런이 sigmoid를 통과되어 가중치와 곱해졌을 때의 범위가 뉴런의 개수가 N이라고 할 때 [-N, N]이 된다.
휴리스틱하게 봤을 때 스케일링을 통하여 레이어를 통과하기 전이나 통과한 후에 분산을 1로 동일하게 해야 한다고 주장한다.
이렇게 되면 네트워크의 모든 뉴런이 비슷한 분포를 가져 수렴 속도를 향상시킨다고 한다.
fan in : input Layer의 뉴런의 수
fan out : output Layer의 뉴런의 수
그러므로 루트 fan in으로 나눠주면 된다. 하지만 여기까지는 forward만 고려한 방법이다. 그래서 backward도 고려해 분산을 2 / (fan_in + fan_out)로 만들어 준다.
uniform distribution에서는 분산이 루트( 6 / (fan_in + fan_out))이 된다.
균등분포의 범위가 [a, b]라고 할 때 분산이 (b - a)^2 / 12가 된다.
근데 분포가 대칭으로 만들려면 [-b, b]의 형태고 b^2 / 3 = 2 / (fan_in + fan_out)이 되므로
최댓값(b)가 루트(6 / (fan_in + fan_out))이 된다.
relu에서는 He initialization인 표준편차가 루트( 2 / fan_in )으로 만들어서 사용해준다.
아래는 수식 유도이다.
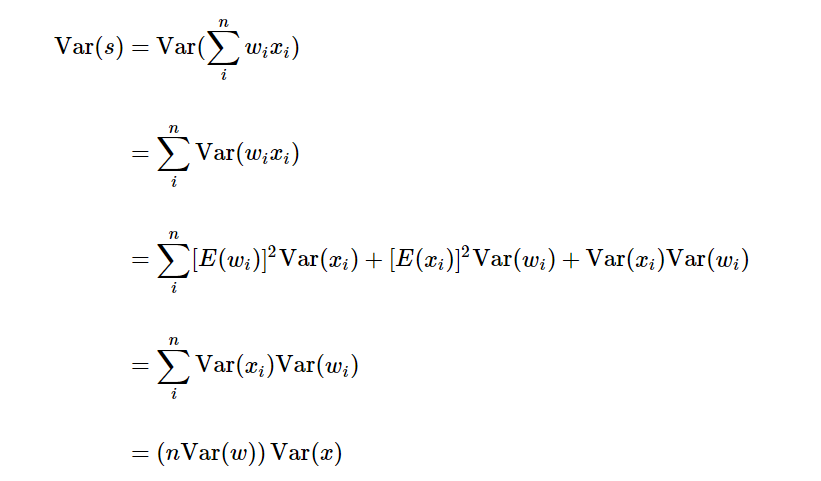
이미지 참조 : https://cs231n.github.io/neural-networks-2/#init
Var(s) = Var(x)로 만들기 위해 Var(w) = 1 / n의 꼴이 나와 fan_in으로 스케일해줘야 한다는 것이다.
