Optimizer

5050·2021년 7월 14일

목록 보기

2/6

optimizer란 머신러닝에서 backpropagation으로 기울기를 구하여 이를 이용해 가중치를 갱신시키는 것이다.

optimizer의 방식에는 여러가지가 있지만 그 중 몇가지만 살펴보도록 하자.

1. Gradient Descent
Parameter를 W라고 뒀을 때 실제값과 네트워크에서 내놓은 예측값과의 차이를 의미하는 loss function $L(W)$ 의 값을 최소화하기 위해 $\nabla_WL(W)$ 를 이용하는 방법이다.
기울기의 반대 방향으로 일정 크기만큼 이동하는 것을 반복적으로 진행하여 $L(W)$ 을 최소화하는 $W$ 의 값을 찾는다.

$W = W - \alpha\nabla_WL(W)$

위의 수식으로 W를 갱신한다. $\alpha$ 는 learning_rate가 된다. 여기서 또 의문이 드는게 그냥 $\nabla_WL(W)$ 이 것을 0으로 두고 풀면 되는건데 왜 굳이 learning_rate를 도입해서 고생을 할까
그런데 이유가 다 있더라.
딥러닝에서는 데이터의 양이 엄청나게 많은데 그거에 대해 0으로 두고 푸는 것보다 위처럼 반복적으로 하는 게 더 효율적이고, 네트워크가 깊어지면서 복잡해져 닫힌 형태(수학적으로 잘 정의해 해석적인 해가 존재하는 형태의 방정식으로 바꿀 수 있는 것)로 나타낼 수 없는 경우 등의 이유가 있다고 한다.

2. Stochastic Gradient Descent

Loss function을 계산할 때에 전체 학습데이터셋을 사용하는 것을 Batch Gradient Descent라고 한다. 하지만 이렇게 한다면 1step이 전체 데이터에 대해 계산해야 하므로 많은 계산량을 필요해 오랜 시간이 걸린다. 이를 방지하기 위해 Stochastic Gradient Descent(SGD)를 이용한다.
전체 학습 데이터 대신 mini batch 일부의 데이터에 대해서만 loss function을 계산한다.
BGD에 비해 다소 부정확할 수 있지만 계산속도가 훨씬 빨라 같은 시간에 더 많은 step을 진행할 수 있고 여러번 진행한다면 GD와 유사하게 수렴한다.
앤드류응 교수는 학습데이터가 2000개 이하라면 그냥 GD로도 빠르게 진행가능하다고 한다.
그리고 메모리를 생각해봤을 때 mini batch size는 2의 승수로 하는 게 좋다고 한다.

3. Momentum

SGD를 통해 더 나은 방법을 찾았음에도 문제는 계속 있었다. 바로 local minima에 빠지는 현상이다.

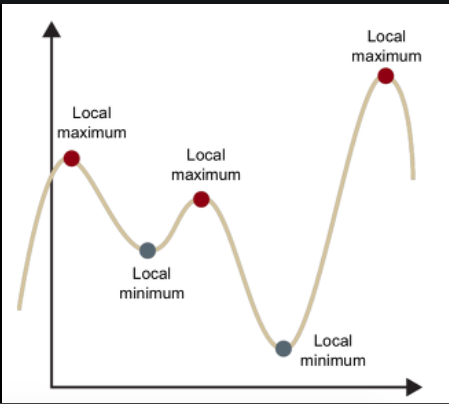
local minima의 개념은 위의 사진을 참고하자. 아까 말한 것처럼 네트워크가 복잡해지면서 weight는 더 고차원으로 갈 것이다. 그에 따라 저런 local minima가 많이 생기는데 SGD는 local minima에서 빠져나올 방법이 없다.

<<하지만 요즘에는 실제로는 딥러닝에서 지역 최소점에 빠질 확률이 거의 없기 때문에 지역 최소점은 크게 중요하지 않다고 한다. 모든 축의 방향으로 f'' > 0이 되어야하지만 그럴 확률이 거의 0이라는 것이다. 위로 볼록, 아래로 볼록이 랜덤하게 발생한다고 가정하면 $1/2^n$ 이다. 거의 critical point는 saddle point고 아니라면 global minimum이거나 global minimum과 유사한 수준의 local minimum이라고 한다. 근데 이 global minumum이라는 주장은 실험적 사례라고 하기 때문에 확실히 global minimum이라고 단정을 지어도 되는 지는 모르겠다.>>

게다가 특정 방향으로는 platue와 같은 평평한 모습이 나올 수 있어 다른 방향으로 진동하는 형태가 나와 학습이 더딘 경향도 있다. 그래서 가속도를 줘 더 효과적으로 학습할 수 있게한다.

$V_t = \gamma$ $V_t-_1+\alpha\nabla_WL(W)$ - notation (1)
$V_t = \beta$ $V_t-_1+(1 - \beta)\nabla_WL(W)$ - notation (2)

$W= W-V_t$

$\beta$ 는 하이퍼 파라미터로 일반적으로는 0.9를 많이 사용하는 것으로 알고 있다.
보면은 B가 커질수록 현재의 기울기를 적게 반영하겠다는 의미이다.

여기서 잘 보면 지수이동평균이라는 개념이 적용됐다고 보여진다.
먼저 단순이동평균이 무엇인지 보면은 주식으로 예를 들자면 N일동안의 평균을 보겠다는 것이다.

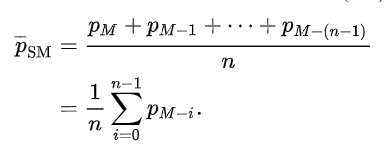
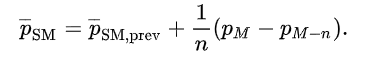
array[100]이 있다면 이것으로 평균을 계산하고 새롭게 들어오는 데이터는 0번째 index부터 바뀌어 계산하는 것이다.
그러면 지수이동 평균은 가중치를 주어 새롭게 갱신되는 기울기에 민감하게 반응하겠다는 것입니다. 물론 $\beta$ 의 값을 어떻게 주냐에 따라 둔감할지 민감할지 조정하는 것이다.
보통 주식에서는 추세를 파악하기 위해 사용하는데 여기서는 이전의 기울기를 보고 모멘텀을 주는 것을 보면 추세를 보고 반영하겠다로 일단 이해해야겠다.

4. AdaGrad

AdaGrad는 가중치를 갱신할 때마다 변수마다 다른 폭으로 학습하게끔 하는 방법이다.
기본적인 아이디어는 학습을 통해 크게 변동이 있었던 가중치는 학습률을 감소시키고 아직 가중치 변동이 별로 없었던 가중치는 학습률을 증가시켜 학습시키자이다.
왜냐하면 많이 변동했던 변수들은 이미 최적값 근처에 있을 확률이 높을 것이기 때문에 작게 유도하는 것이라고 생각이 든다.

$H_t = H_t-_1 + (\nabla_WL(W))^2$
$W = W - \alpha\nabla_WL(W) /\sqrt{H}$

$H$ 에 지속적으로 기울기를 제곱해 더함으로서 학습률을 감소시킨다.
하지만 계속 학습하다보면 $H$ 가 너무 커져 학습이 안될 수 있다.

5. RMSProp

AdaGrad의 $H$ 가 너무 커져 학습이 안되는 부분을 보완하여 고친 알고리즘이다.
창시자인 제프리 힌톤이라는 분이 온라인 강의에서 처음 소개한 방식이라고 합니다.
AdaGrad의 $H$ 부분에서 단순 합이 아니라 지수이동평균을 적용한 방법이다.
AdaGrad처럼 $H$ 가 무한정 커지지 않으면서 최근 변화량의 변수간 상대적인 크기는 적용할 수 있다.