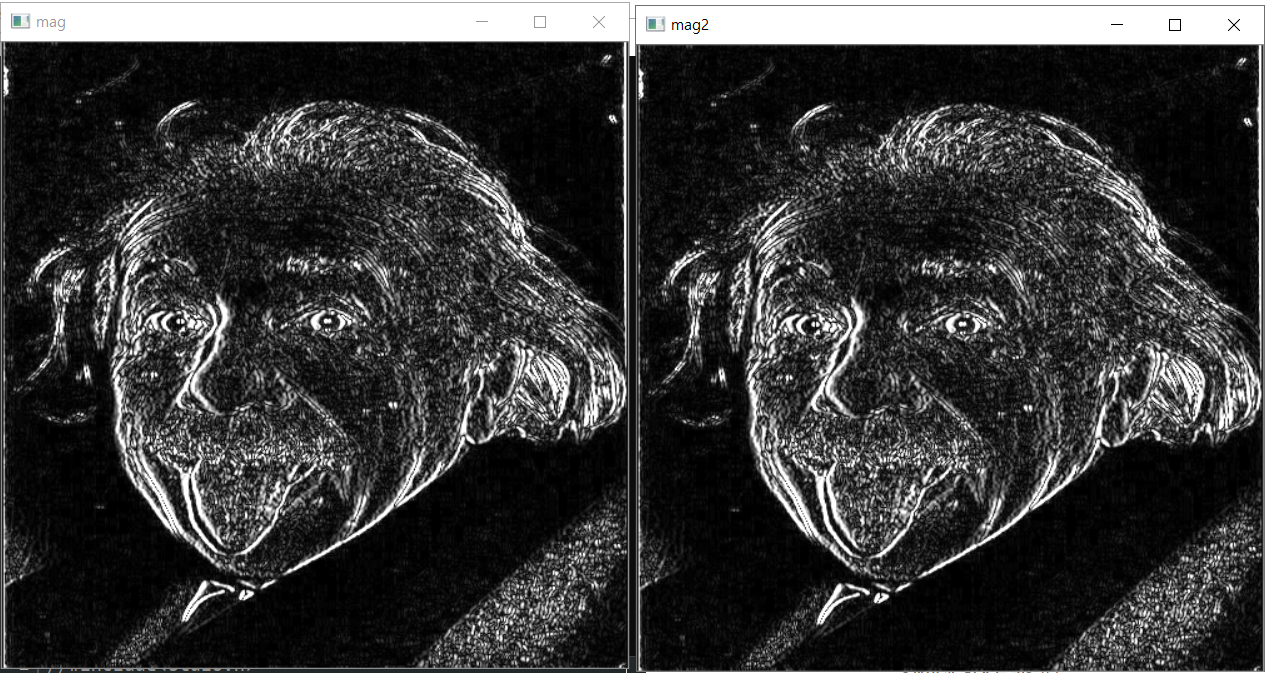
영상에서 에지만 있어도 원래 영상을 거의 그대로 해석할 수 있다.
게다가 에지 영상은 이진 영상이므로 원래 영상에 비해 필요한 메모리가 적다
그러므로 에지는 매우 유용하다. 그럼 에지를 어떻게 검출할까
물체의 경계에서는 명암값에 급격한 변화가 일어난다.
즉, 에지는 영상의 명암, 컬러 또는 텍스처와 같은 특성이 급격히 변하는 지점이다.
모든 에지 검출 알고리즘은 변화를 측정하고 변화량이 큰 곳을 에지로 취급하는 원리를
따른다고 한다.
수학에서 변화를 측정하는 기초 이론은 미분이다.
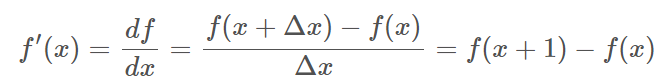
미분을 배울 때에는 연속 공간에서 배웠지만 영상은 연속공간이 아닌 이산 공간이다.
그래서 위와 같이 근사화를 할 수 있다. 영상에서는 가장 작은 단위가 1이기 때문이다
(-1, 1)을 컨볼루션하는 것과 같다.
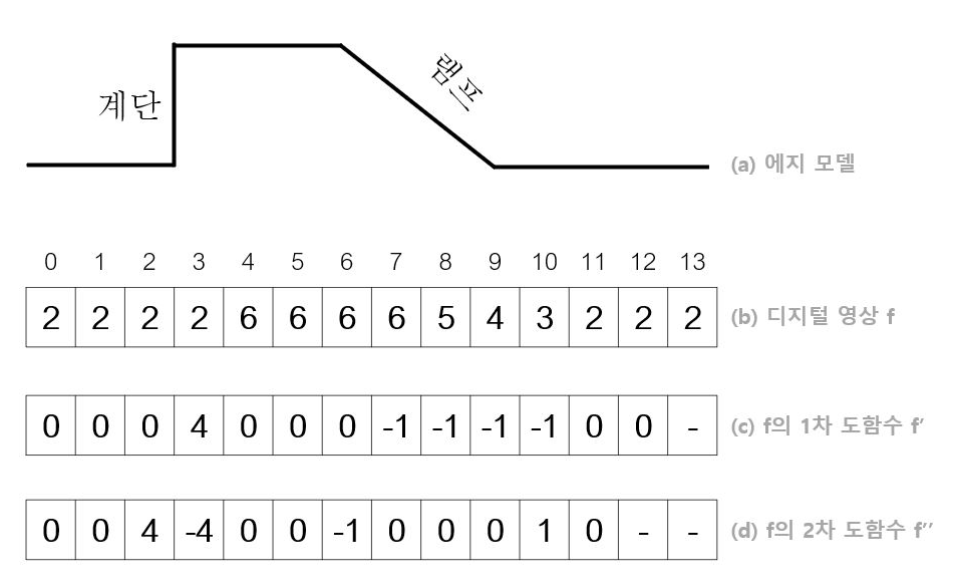
위의 이미지에서 보면 급속한 변화가 있는 지점의 값이 크고 변화가 작은 곳이 값도 작다.
실제 영상에서는 계단 에지보다는 주로 램프 에지가 나타난다.(초점이 안맞거나 곡면같은 것은
경계 부근에서 명암이 서서히 변한다.)
그래서 위의 램프에지에서 정확한 에지의 위치를 찾는 것이 어렵다.
2차 미분으로 확장한다면,
계단에지에서나 램프에지에서 영교차가 발생한다.
이 원리를 이용하면 1차에서 봉우리를 찾고, 2차에서는 영교차를 찾으면 된다.
그리고 에지 검출에서 잡음도 고려를 해야하는데, 이상적으로는 차이가 딱딱 크게 나야하지만
잡음으로 인해 값이 조금씩 차이날 수 있다.
이전에 포스팅했던 스무딩 연산을 적용하면 쉽게 해결할 수 있다.
스무딩 연산은 3*3 이상의 연산자를 사용하므로 에지 연산자도 크기를 키운다.
식에 의하면 마스크는 -1/2와 1/2를 가져야 하지만 상대적인 크기가 중요하므로
(-1, 0, 1)로 한다.
이 것을 2차원으로 확장해 편도함수를 취해 그레디언트 벡터를 형성한다.
이론 적으로는 위처럼 나오지만, 잡음에 대처하기 위해 d*d크기의 정방형으로 확장해 아래와 같이 사용한다. 아래는 잘 알려진 세 종류의 연산자이다.
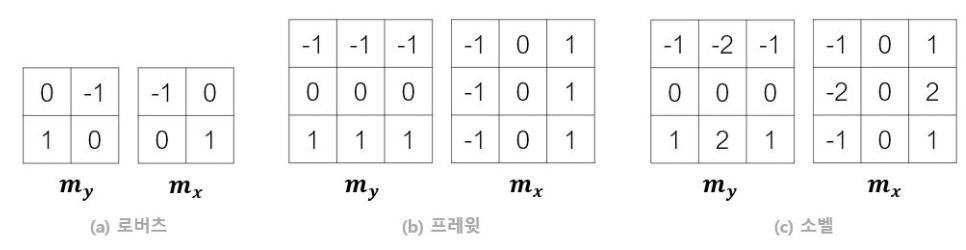
로버츠는 너무 작고, 대칭이 아니라 잘 사용되지 않는다.
프레윗 연산자는 x방향 미분값을 계산할 때 아래와 윗행까지 고려해 스무딩 효과가 내포되어 있다.
소벨 연산자는 가까운 화소에 더 큰 가중치를 준다. 소벨이 가장 널리 쓰인다.
그레디언트 벡터는 에지 강도와 방향을 가진다.
에지 강도 :
에지 방향 :
에지 강도는 해당 픽셀이 에지일 가능성 또는 신뢰도를 나타내는 값이다.
filter2D를 활용해 필터만 정해줘서 구할 수 있다.

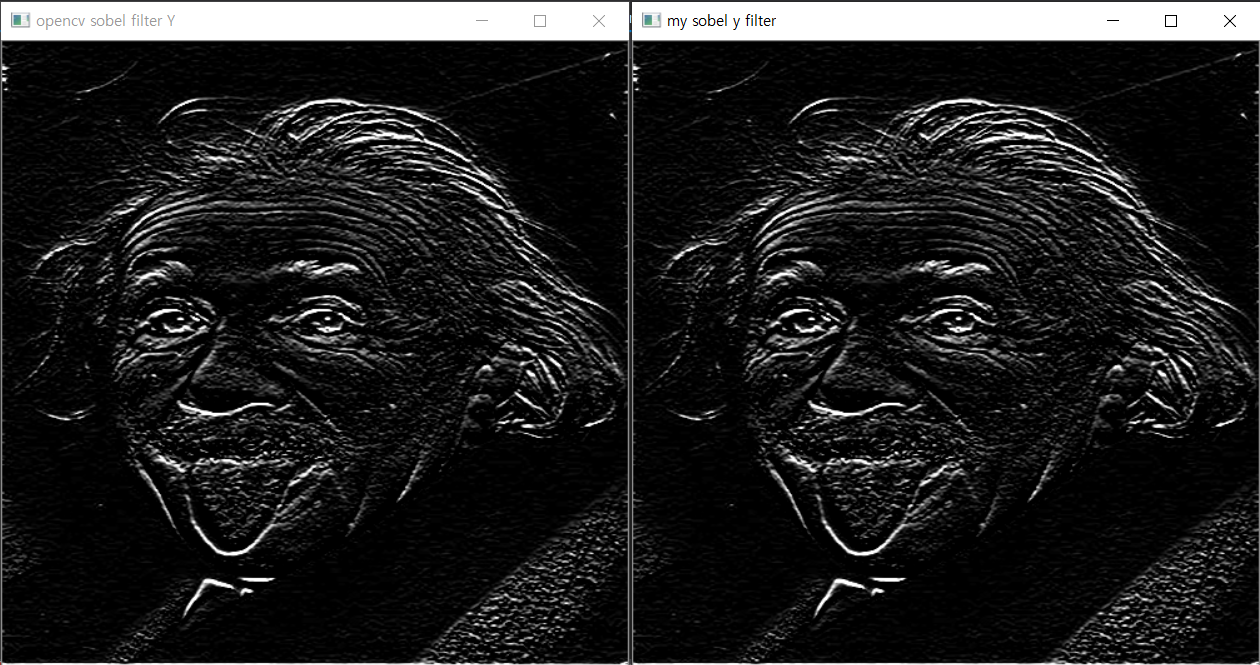
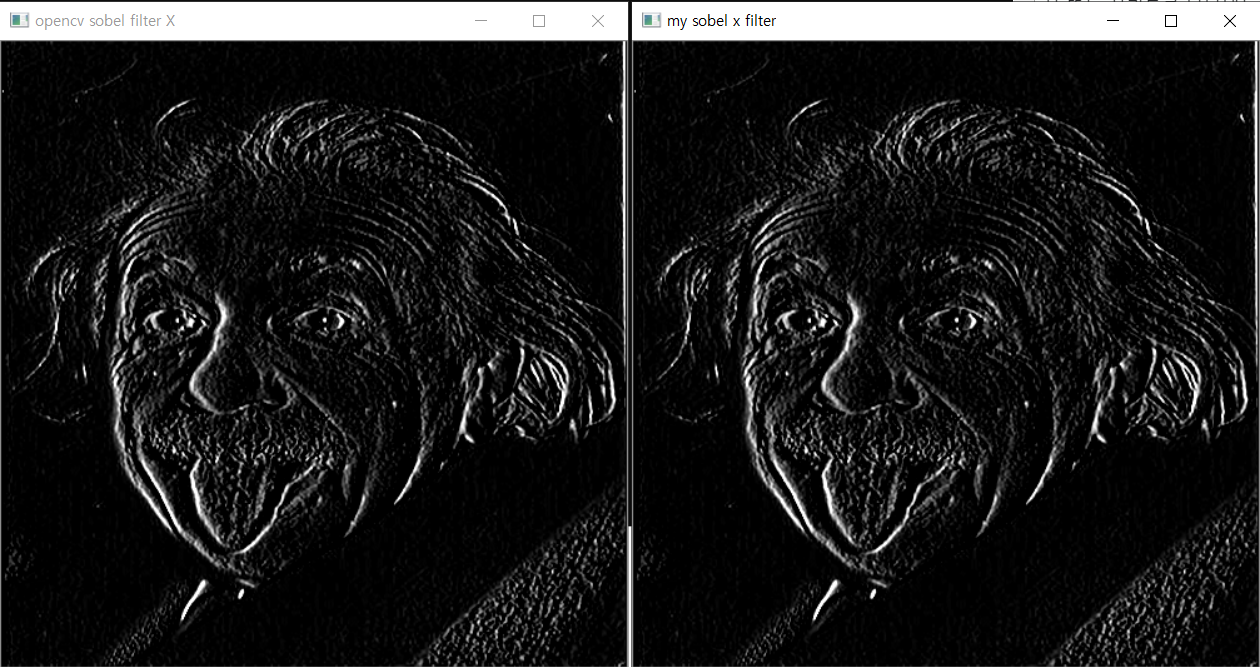
opencv를 활용한 sobel

opencv를 활용한 에지 강도와 에지 방향

직접 magnitude구하기

gy
gx
magnitude