영교차이론

이전 포스팅에서 가우시안 마스크를 아주 가볍게 소개한 적이 있다.

에지 연산에서 미분연산을 적용하기 전에 가우시안을 스무딩하는 전처리 과정을 중요하게 생각했는데 가우시안 스무딩은 두 가지 효과를 제공한다.

1. 잡음 대처 (미분은 잡음을 증폭하므로 스무딩은 중요하다)
2. $\sigma$값을 조절해 다중 스케일 효과를 얻을 수 있다.

$\sigma=0.5$일 때 1차 미분과 2차 미분 모두에서 영교차가 선명하게 나타난다
하지만 표준편차 $\sigma$의 값을 키운다면 영상의 디테일이 사라져 큰 물체의 에지만
추출되고 작게 한다면 물체의 디테일에 해당하는 에지까지 추출할 수 있다.

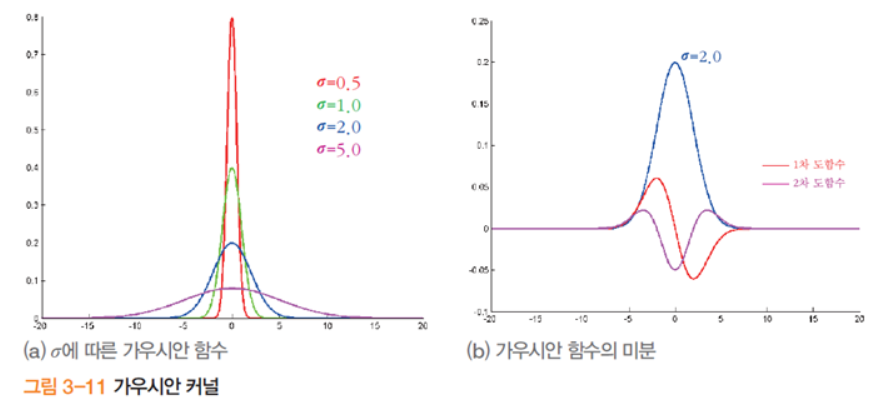
위의 그림을 보면 $\sigma$가 클수록 좌우로 넓게 퍼지며 봉우리가 낮아진다. 즉, 가우시안의 영향력 범위가 넓어진다.
$\sigma = 2.0$일 때, x += 6의 바깥쪽은 0에 가까우므로 크기가 13정도인 마스크를 만들어 적용한다.
이보다 작은 마스크는 오차가 크기 때문에 영상 처리의 품질이 떨어지고, 크면 시간효율만 떨어지고 얻는 것이 없다.
마스크의 크기를 결정하는 대략적인 규칙은 $6\sigma$와 같거나 큰 정수 중에 가장 작은 홀수를 마스크의 크기로 취하는 것이다.

LOG 필터

1. 가우시안 스무딩
2. 라플라시안 연산자를 적용해 2차 미분
3. 영교차를 찾아 에지 설정하고 나머지는 비에지로 설정

$\nabla^2 f(y,x) = \partial^2f/\partial y^2 + \partial^2 f/\partial x^2$

sobel에서 했던 것을 활용하여 근사하면
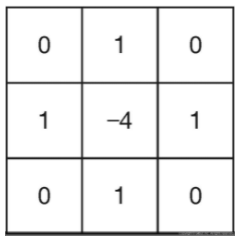
$\nabla^2 f(y, x) = (f(y+1, x) + f(y-1,x) -2f(y,x)) + (f(y, x+1)+f(y, x-1) -2f(y,x))$
$=f(y+1,x)+f(y-1,x) + f(y, x+1) + f(y, x-1)-4f(y, x)$

$LOG(y, x) = \nabla^2 (G(y,x) \circledast f(y, x)) = (\nabla^2 G(y,x))\circledast f(y, x)$
결합법칙을 이용하여 위처럼 수식을 변경해 LOG필터라고 부른다.

$\nabla^2 G(y, x)=((y^2 + x^2-2\sigma^2)/\sigma^4)G(y,x)$

영교차 검출

1.여덟개의 이웃 중에 마주보는 동-서, 남-북, 북동-남서, 북서-남동의 화소 네 쌍을 조사한다. 그 중 두 개 이상이 서로 다른 부호를 가진다.
2. 부호가 다른 쌍의 값 차이가 임계값을 넘는다.