캐니 에지

현재 가장 널리 사용되는 에지 검출 연산자이다.
기존의 휴리스틱한 방식을 뛰어넘어, 에지 검출을 최적화 문제로 취급했다.
에지 알고리즘이 갖추어야 할 세 가지 기준을 아래와 같이 제시했다.

1. 최소 오류율 : 거짓 긍정과 거짓 부정이 최소여야 한다. 없는 에지가 생성되거나 있는 에지를 못 찾는 경우를 최소로 유지해야 한다.

2. 위치 정확도 : 검출된 에지는 실제 에지의 위치와 가급적 가까워야 한다.

3. 에지 두께 : 실제 에지에 해당하는 곳에는 한 두께의 에지만 생성해야 한다.

캐니는 기준에 부합하는 목적 함수를 만든 후, 이 함수를 최적화하는 연산자 설계를 시도했다.
하지만 위의 조건을 모두 만족하는 연산자를 찾아내는 것은 불가능한 일이다.
따라서 1차원 계단 에지에 화이트 잡음이 첨가된 상황을 가정하고 최적화 작업을 하였다.
그 결과 가우시안에 1차 미분을 적용한 연산자가 최적임을 수학적으로 증명하였다.

하지만, 1차원에서 도출한 결과를 2차원으로 확장하기 위해서는 그레디언트 방향을 알아내어 그 방향으로 미분을 수행해야 하는데 그것을 소벨이나 프레윗같은 마스크를 이용해 그레디언트 방향을 구하는 것을 근사화할 수 있고 오류는 허용할 수 있는 범위에 있다는 사실까지도 증명했다.
그리고 에지를 얇게 바꾸는 비최대 억제라는 단계를 추가했다.
마지막으로 거짓 긍정 에지를 제거하는 이력 임계값 단계를 적용한다.

요약한다면
1. 입력 영상에 가우시안 스무딩을 적용한다.
2. 가우시안 스무딩된 이미지에 소벨 연산자를 적용하여 에지 강도와 방향맵을 구한다.
3. 비최대 억제를 적용하여 얇은 두께의 에지 맵을 만든다.
4. 이력 임계값을 적용하여 거짓 긍정을 제거한다.

비최대 억제

비최대 억제 알고리즘은 자신의 이웃보다 크지 않은 화소를 억제한다. 억제란 에지가 아닌 것으로 결정하는 것을 의미한다. (자신의 두 이웃보다 크면 에지로 결정)
이웃을 정하는 방법은 아래와 같다.

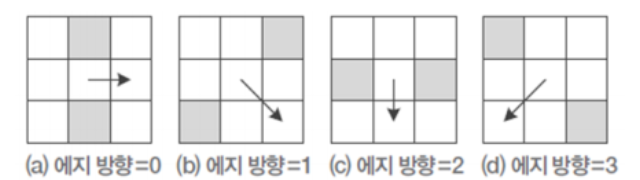
방향 4, 5, 6, 7은 각각 0, 1, 2, 3 동일하다.

비최대 억제를 함에도 거짓 긍정 에지가 많이 포함되는데, 임계값을 정해두고 임계값보다 작다면 거짓 긍정으로 보고 제거하는 방법이 있는데 tradeoff가 일어난다.
T를 높게 설정한다면 거짓 긍정을 잘 제거하지만 에지 강도가 낮은 진짜 에지도 지워지기 때문이다. 반대의 경우도 마찬가지다.

캐니에지에서는 두 개의 임계값을 사용한다.
높은 임계값에서 시작하여 신뢰도가 높은 화소만 에지 추적을 시작한다.
시작 화소가 정해지면 낮은 임계값을 넘는 화소를 대상으로 에지를 추적한다.
이웃 화소가 추적 이력이 있다면 자신이 신뢰도가 낮더라도 에지로 간주된다.
높은 임계값을 낮은 임계값의 2~3배로 할 것으로 권고된다.

가우시안 이미지에 소벨 연산자 적용

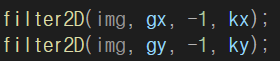
에지 방향과 강도 구하기

방향은 에지의 방향은 그레디언트와 수직이므로 90도를 더해주고 방향을 정할 때에 음수가 나온다면 180도를 더해진 각과 동일하므로 더한 것으로 정한다.

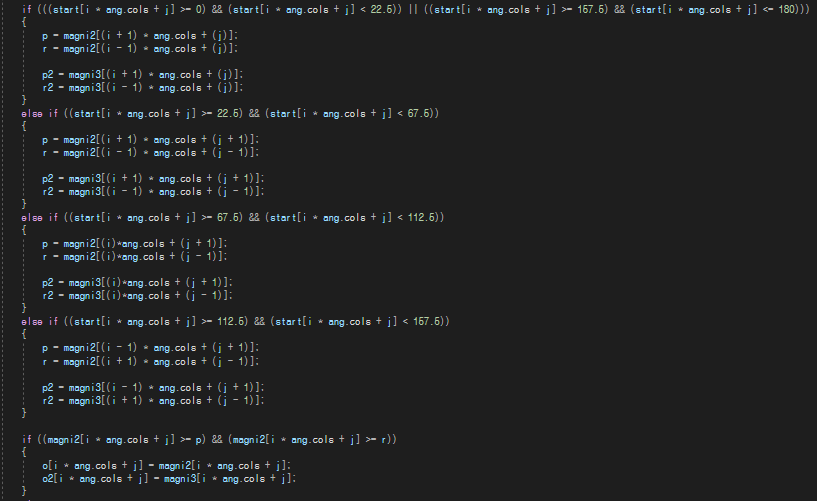
비최대 억제

이력 임계값을 이용한 에지 추적

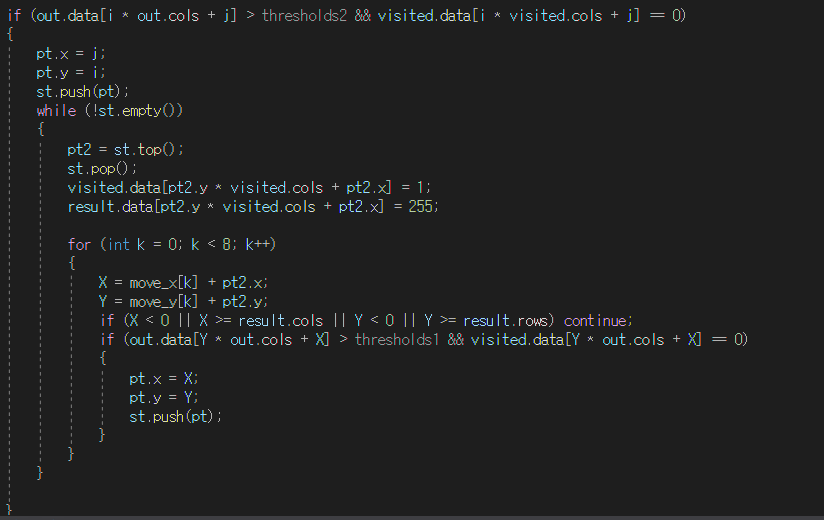
재귀호출로 진행시 터지는 상황이 발생해 스택으로 대체했다.
OpenCV를 활용한 canny edge

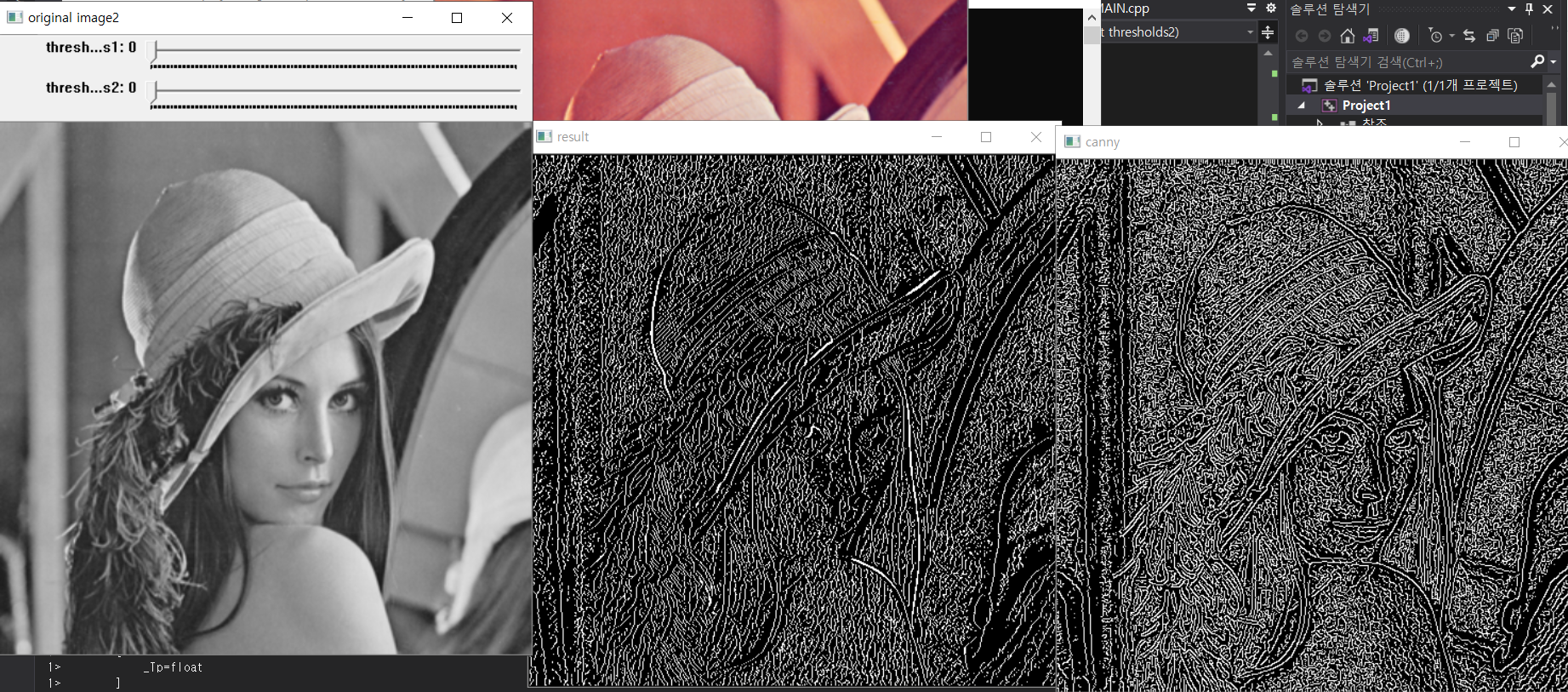
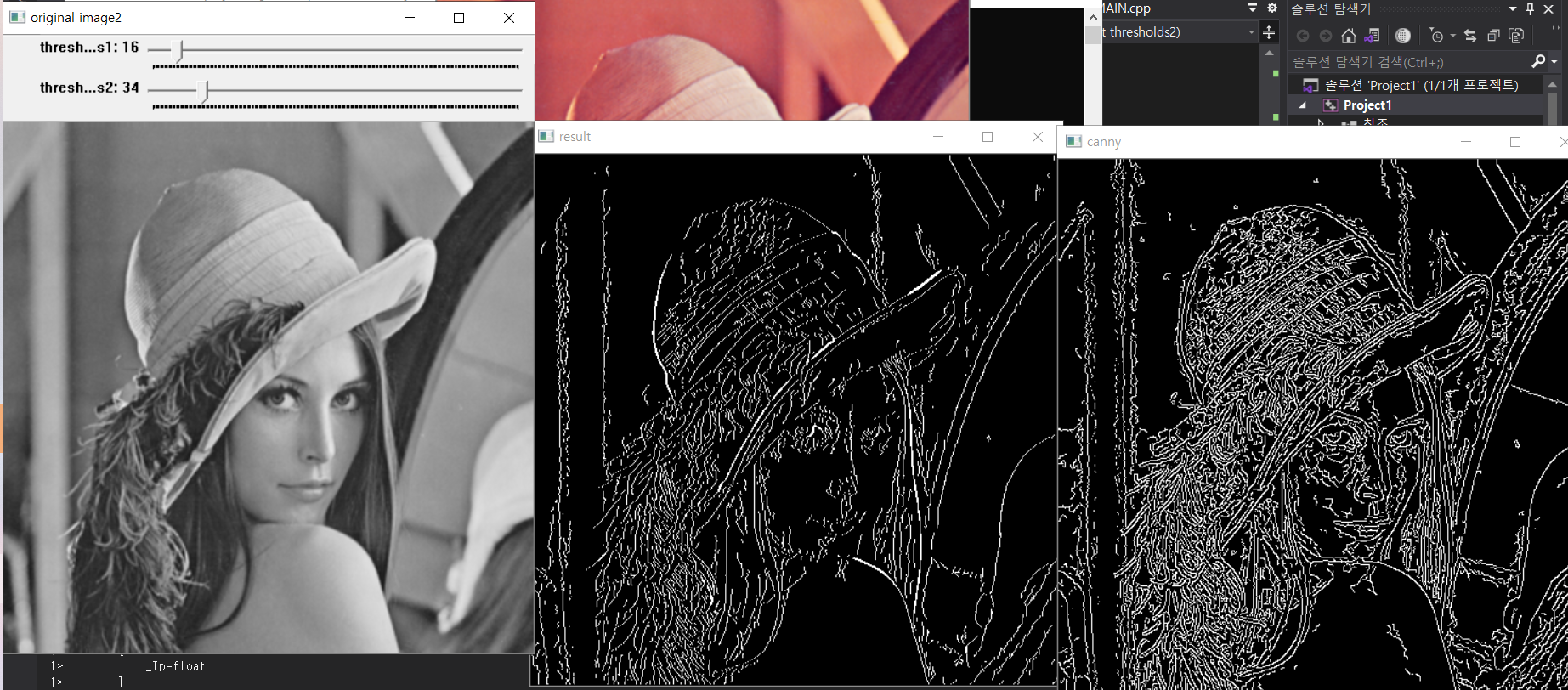
직접 구현한 것과 OpenCV의 차이가 다소 존재한다.

트랙바를 적용하여 임계값을 조절했고
낮은 임계값을 높이면 큰 에지? 안의 작은 자글자글한 에지들이 사라지는 경향이 있고
높은 임계값을 높인다면 자글자글한 에지들도 일부 사라지지만 낮은 임계값에서 지울 수 없는 큰 에지들이 사라지는 경향을 발견할 수 있었다.

컬러에지

컬러에지에서는 가장 쉽게 사용할 수 있는게 RGB각 채널에 대해 적용하고 다시 RGB로 합치는 방법이 있지만, 각 채널의 에지 방향에 따라 다른 값을 부여해야 하므로 적절치 않을 수 있다.

이러한 상황을 고려하여 디 젠조라는 사람이 아래와 같은 방법을 제안하였다.

$g_{yy} = (d_{yr})^2 + (d_{yg})^2 + (d_{yb})^2$
$g_{xx} = (d_{xr})^2 + (d_{xg})^2 + (d_{xb})^2$
$g_{yx} = d_{yr}d_{xr} + d_{yg}d_{xg} + d_{yb}d_{xb}$

에지 방향 $D(y, x) = arctan(2g_{yx}/(g_{xx} - g_{yy}))/2$
에지 강도 $S(y, x)$ = $\sqrt{0.5 * ((g_{yy} + g_{xx}) + (g_{xx} - g_{yy}) * cos(2D(y, x)) + 2g_{yx}sin(2D(y,x)))}$

이미지 참조 : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=kss9409&logNo=221538477716

내용 참조 : 컴퓨터 비전(저자 오일석)