✍ Tree ?
: 계층적 구조를 나타내는 자료구조이며 비선형 자료구조이다.
부모와 자식관계의 노드들로 이루어져있으며 한 개 이상의 노드로 이루어져있다.
📝 Tree의 용어
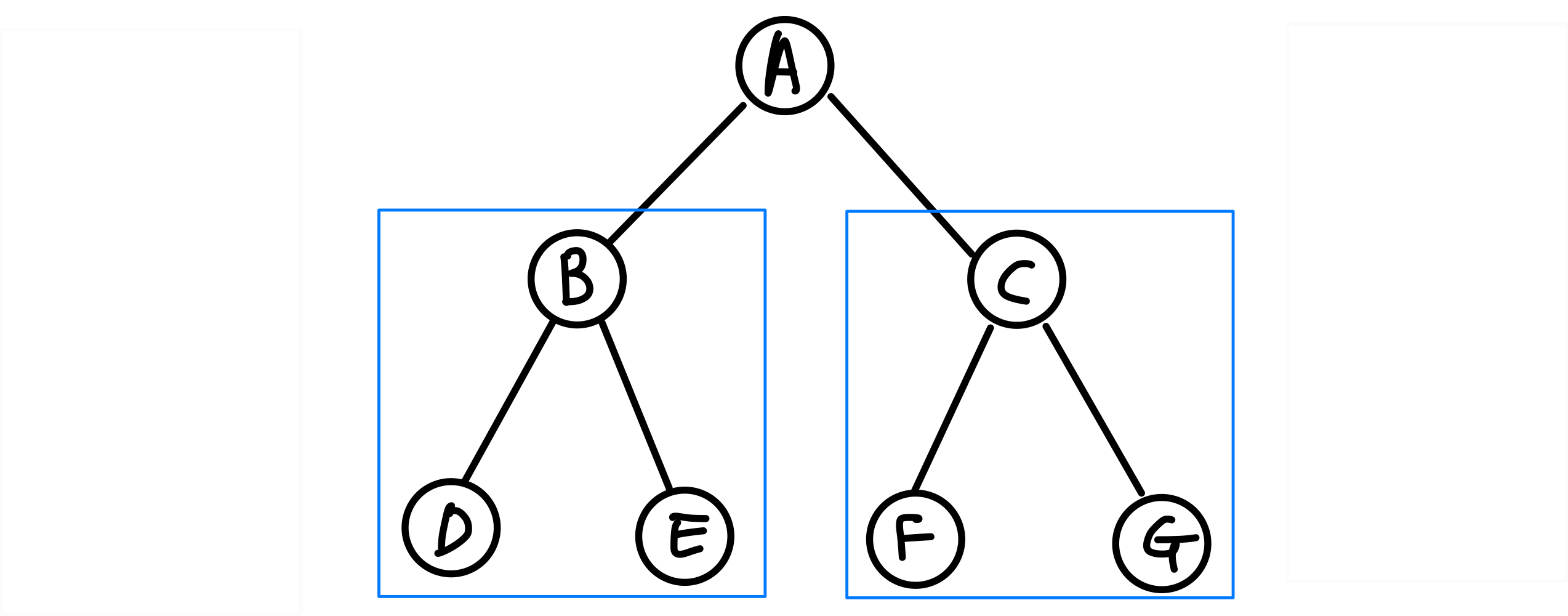
루트노드 : 맨 위에 있는 A를 가리킨다
서브트리 : BDE와 CFG를 가리킨다. 그림의 파란박스
간선 || 에지(edge) : 루트와 서브트리는 선으로 연결되는데, 이때의 선
부모노드 : A는 B의 부모노드이다. B는 D와 E의 부모노드이다
자식노드 : B는 A의 자식노드이다. D와 E는 B의 자식노드이다
단말노드 : 자식 노드가 없는 노드를 말함(D,E,F,G)
차수 : 어떤 노드가 가지고 있는 자식 노드의 개수
(트리의 차수 : 트리가 가진 노드의 차수 중 가장 큰 차수, 위 그림은 2)
레벨 : 트리의 각층에 번호를 매기는 것, 위 그림은 3레벨(위에서부터 1,2,3)
✍이진트리
: 가장 많이 사용되는 트리의 형태. 모든 노드가 2개의 서브트리를 갖는 트리로 최대 2개까지의 자식 노드를 가질 수 있다.
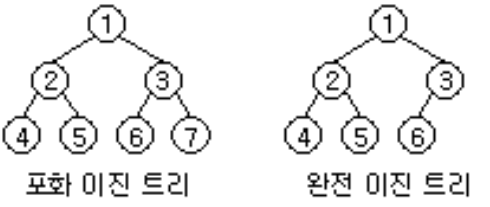
1. 포화이진트리 : 레벨에 노드가 꽉 차있는 이진트리. 정확하게 2^k-1개의 노드를 가진다.
2. 완전이진트리 : 높이가 k인 트리에서 레벨 1부터 k-1까지는 노드가 모두 채워져있고 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워진 이진트리.
📝이진트리의 표현
1. 배열 표현법
이진트리의 높이가 k이면 2^k-1개의 공간을 연속적으로 할당.
인덱스 0은 사용하지 않는 편이 계산에 편리해서 1부터 사용.
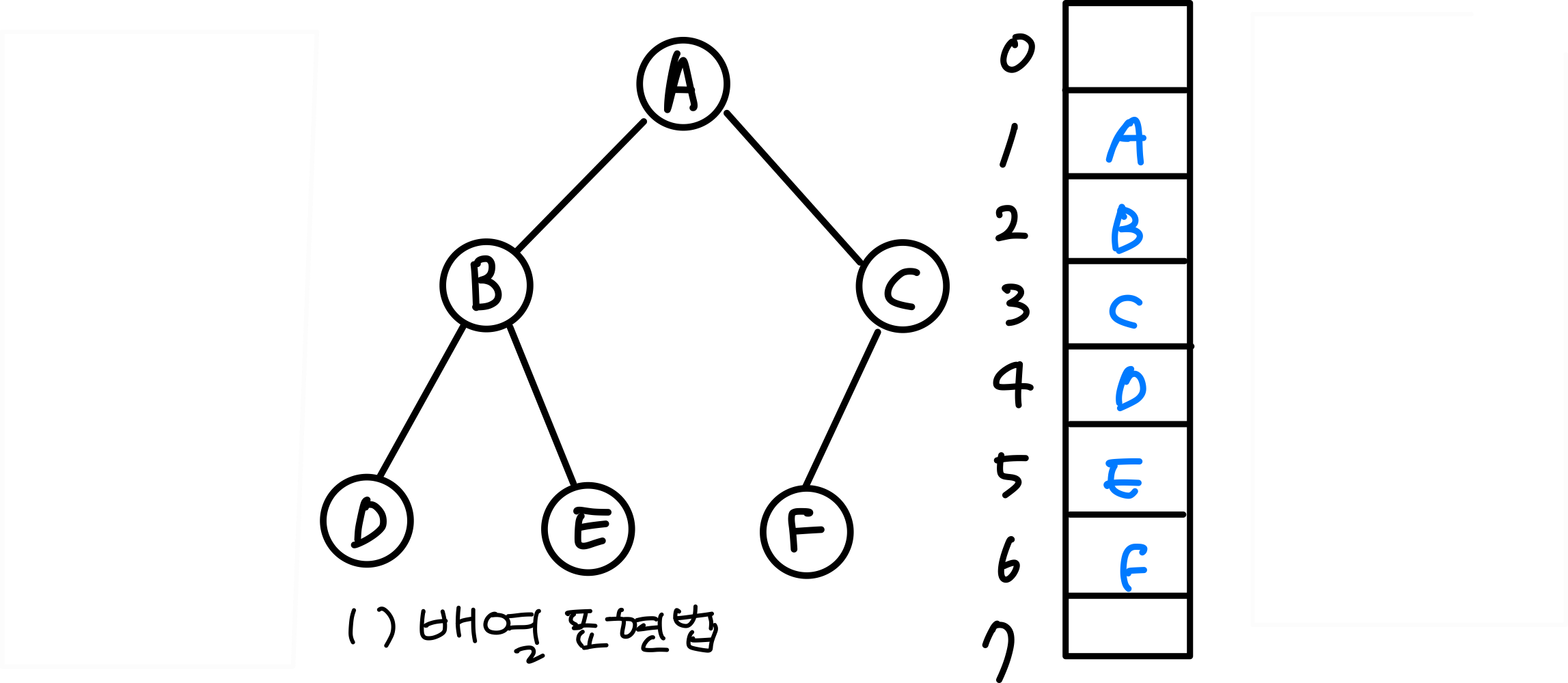
노드 i의 부모 노드 인덱스 = i/2
노드 i의 왼쪽 자식 노드 인덱스 = 2i
노드 i의 오른쪽 자식 노드 인덱스 = 2i+1
ex) D노드의 부모를 알고싶으면 D노드의 인덱스(4) /2를 해주면 된다
2. 링크 표현법
링크 표현법에서의 이진트리 노드의 구조이다.
가운데는 data값을 담고있다
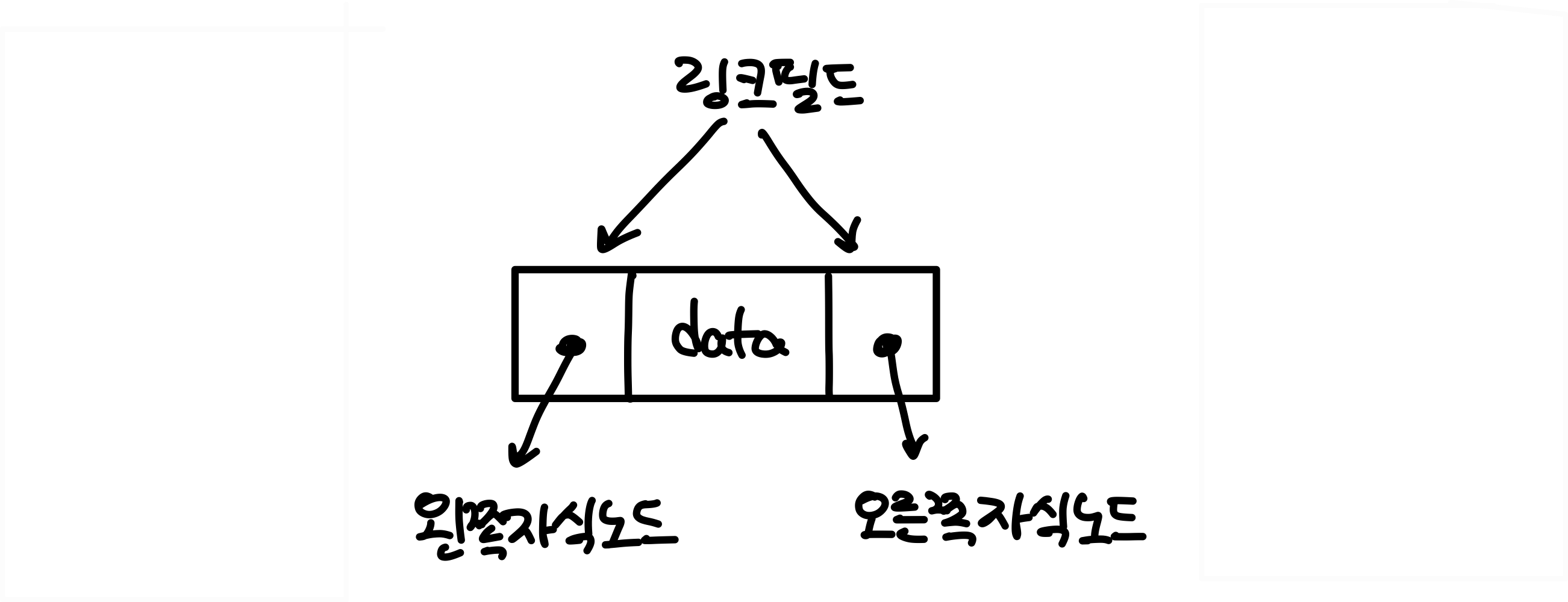
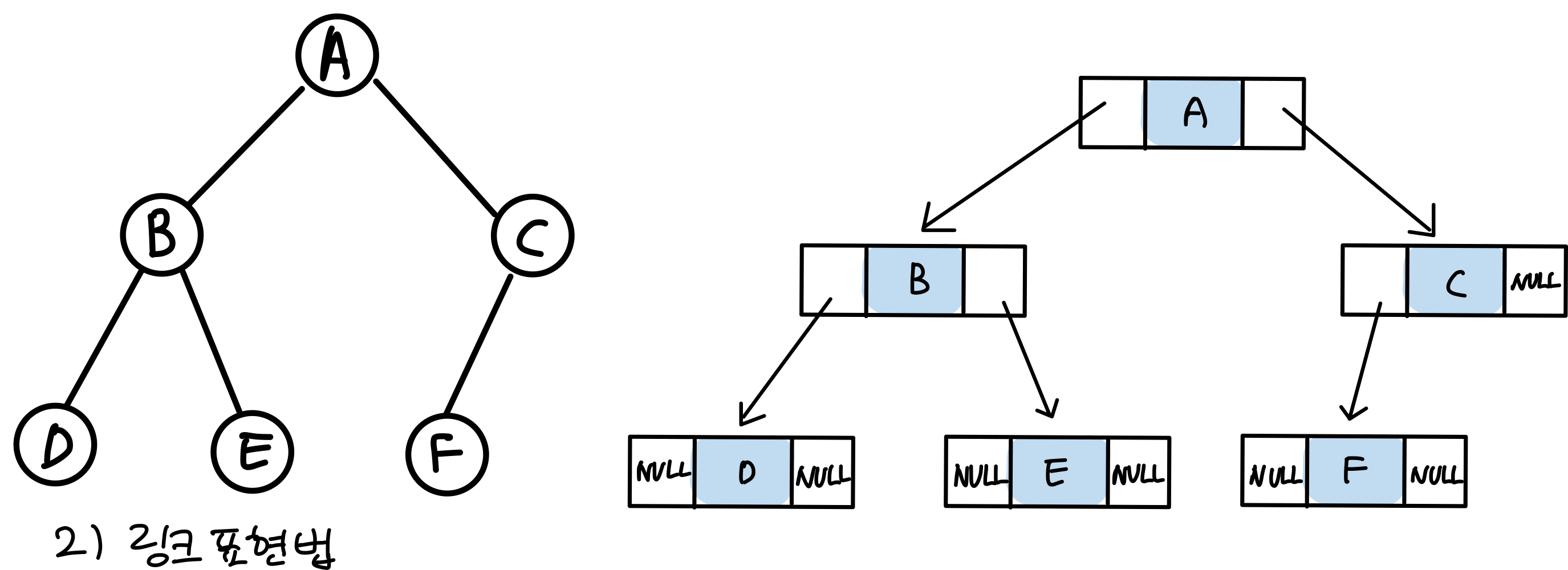
보다시피 이진트리는 노드들의 집합이다.
링크표현법으로 이진트리를 구현하기 위해서는 노드구현->트리구현 순서이다
📝이진트리 구현(링크표현법으로)
//노드 구현
class BinaryNode {
int data; //트리에 저장할 데이터
BinaryNode* left; //왼쪽 자식 노드의 포인터
BinaryNode* right; //오른쪽 자식 노드의 포인터
public:
BinaryNode(int val=0,BinaryNode* l=NULL,BinaryNode* r=NULL):data(val),left(l),right(r){} //생성자
void setData(int item){
data = item;
} //데이터 값 저장할때
void setLeft(BinaryNode* n){
left = n;
} //왼쪽 자식 노드의 주소를 저장
void setRight(BinaryNode* n){
right = n;
} //오른쪽 자식 노드의 주소를 저장
int getData() { return data; }//현재 저장된 데이터 값 불러올때
BinaryNode* getLeft() { return left; } //왼쪽 노드의 주소값 보여줌
BinaryNode* getRight() { return right; } //오른쪽 노드의 주소값을 보여줌
bool isLeaf() { return (left == NULL) && (right == NULL); } //단말노드인지 아닌지 확인하는 함수
};//위의 노드로 구성된 이진트리 구현
class BinaryTree {
BinaryNode* root;
public:
BinaryTree() {}
void setRoot(BinaryNode* n) {
root = n;
}//트리의 루트를 정하는 메소드
BinaryNode* getRoot() {
return root;
}//현재트리의 루트를 불러올때
bool isEmpty() { return root == NULL; } //루트노드의 존재여부
int getCount() { return isEmpty() ? 0 : getCount(root); } // 1.
int getCount(BinaryNode* node) {
if (isEmpty()) return 0;
else {
if (node == NULL) return 0;
return 1 + getCount(node->getLeft()) + getCount(node->getRight());
}
}
int getHeight() { return isEmpty() ? 0 : getHeight(root); } //2.
int getHeight(BinaryNode* node) {
if (node == NULL) return 0;
int hLeft = getHeight(node->getLeft());
int hRight = getHeight(node->getRight());
return (hLeft > hRight) ? hLeft + 1 : hRight + 1;
}
1. getCount(): 트리에 존재하는 노드의 총개수를 구하는 함수. return문에 집중하면 되는데, 처음 들어가는 루트노드의 왼쪽 자식과 오른쪽 자식이 새로운 루트노드가 되어 getCount()함수에서 개수를 다시 센다.
(이진트리함수의 개수세기,높이세기, 단말노드갯수구하는 함수는 대부분 순환을 이용하여 해결할 수 있다)
2. getHeight(): hLeft변수는 왼쪽 노드의 높이를 세는 함수이다.
(순환이 함수 중간중간 일어나서 헷갈릴 수 있으므로 직접 손으로 그려서 이해해보는 걸 추천한다)
트리의 구조를 이해하는 것도 좋지만 처음부터 구현할 필요는 없다 ㅎㅎ 다음 글에서는 STL을 사용하여 트리를 활용하는 글을 작성해 볼 예정이다 !
