앞에서 T-test는 2개 집단을 비교할 때 사용한다고 했었다.
이 표본 집단의 수가 2개 이상 일 때는 ANOVA Test(분산분석)을 사용한다.

💡 분산분석

• 두 집단 이상의 평균 간의 차이를 검증하는 방법으로 T-검정을 일반화한 분석법이다.
  즉, 집단 간의 평균들의 분산과 집단 내 관측지들의 분산을 비교해서 집단간의 차이를 검증할 수 있기 때문에 분산값들을 이용하여 집단간의 평균의 차이를 검정하는 것이다.

* 그룹이 3개 이상 일때 t-test를 사용하면 1종오류 발생 가능성이 커진다.
그룹이 3개일 때 (t-test하고자) 2개 그룹씩 비교하면 3Combination2 즉, 총 3번 비교가 이루어지는데
유의수준을 5%로 잡았을때 Bonferroni에 의하면 1종오류 가능성이 Max 15%까지 커진다고 한다.

* T-검정에서는 T-분포를 통한 T-통계량을, ANOVA는 F-분포를 통한 F-통계량을 이용한다.

ANOVA 분석의 가설

귀무가설(H0) : μ1=μ2=μ3
대립가설 (H1) : not H0 (적어도 한 가지는 다르다.)

ANOVA는 각 집단의 평균값 차이가 통계적으로 유의한지 검증한다. 이 때, 분산을 사용해서 확인하게 되는데, 집단 간 분산 / 집단 내 분산으로 나눈 값이 유의 임계치를 초과하는가에 따라 집단 간 평균 차이를 검정하는것이다.

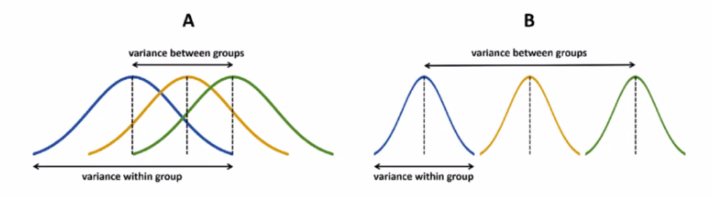
파란색 집단의 평균을 x1, 노란 x2, 녹색 x3 라고 해보자.
x1, x2, x3의 평균을 구해 X라고 하면, ANOVA 분석을 통한 F-value는 다음과 같이 계산한다.

집단 간 분산 : (x1-X)^2 + (x2-X)^2 + (x3-X)^2 / 집단수-1 (즉, 2)
집단 내 분산 : {개별 데이터 값 - 각 평균(x1, x2, x3)}^2 / 관측데이터 수 - 3(집단 수)

결국 해당 그림에서는 B의 F-value가 더 크게 나타날 것이다.

그림을 보고 천천히 생각해보면 이렇게 되기 때문이다.

집단 간 분산(variance between groups)는 B > A
집단 내 분산(variance within group)은 A > B

이렇게 도출된 F-value 값은 특정 값 보다 클수록 H0를 기각하게 된다.

📖 Python

import scipy

scipy.stats.f_oneway(data1, data2, data3)
# (F-statistic, p-value)