T-test는 표본 집단의 평균을 비교할 때 사용하는 검정 방법이었다.
카이제곱검정(Chi-squared test)는 표본집단의 분포/빈도를 비교할 때 선택하는 방법이다.

💡 카이제곱검정

• 카이제곱 검정은 하나 또는 더 많은 범주형 변수의 교차표에서 예측 빈도(expected frequency)와 관측 빈도(observed frequency) 사이의 차이가 통계적으로 유의한지 결정하는 검정이다.
• 범주형 데이터 검정에 사용되며, 관측된 빈도와 기대빈도의 차이를 봄으로써 하나의 확률모형이 전반적으로 자료를 얼마나 잘 설명하는지 검정하는데 사용한다.

카이제곱 식

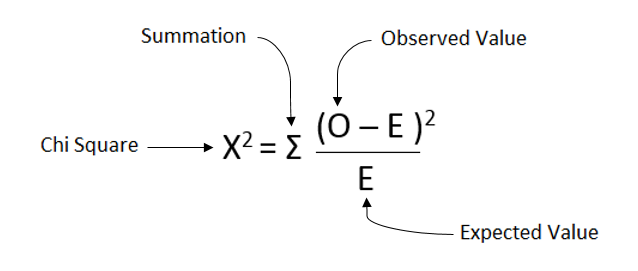
O = 관찰 빈도(Observed Frequency), 자료의 값
E = 기대 빈도(Expected Frequency), 기대 값
df(자유도) = 범주의 개수 - 1

✍️ 적합도 검정(one sample chi-squared test)

• 주어진 데이터(표본 집단)이 특정 분포/빈도와 동일한 분포를 나타내는지에 대한 가설 검정

H0 = 데이터 분포가 특정 분포와 동일하다.
H1 = 데이터 분포가 특정 분포와 동일하지 않다.

📖 Python

from scipy.stats import chisquare

chisquare( data, axis = None )

✍️ 독립성 검정(two sample chi-squared test)

• : 두 데이터(표본집단)의 분포가 동일한지 확인 -> 연관성이 있는지! 여부에 대한 가설 검정

*종속적인 데이터의 경우 분석의 의미가 없어질 수가 있다.
독립 변수들 간에 서로 영향을 준다면 각 변수와 종속변수 간의 관계 파악이 어렵기 때문!
그래서 데이터가 독립적인 것은 중요한 의미를 가진다.

H0 = 두 데이터의 분포는 연관성이 없다. (독립적이다.)
H1 = 두 데이터의 분포는 연관성이 있다. (독립적이지 않다.)

📖 Python

from scipy.stats import chi2_contingency

chi2_contingency( data, correction=False )


# scipy.stats.chi2_contingency(observed, correction=True, lambda_=None)
# observed: array_like