T-test에 들어가기 전에 Z-분포와 T-분포의 관계를 먼저 설명하고자 한다.

Z-분포 (평균=0, 분산=1, 정규분포)
T-분포 (평균=0, 분산>1, 정규분포)

Z-분포는 표분의 갯수가 충분 할 때(30개 이상) 표준화 과정을 거친 정규분포 즉, 표준정규분포 이다.
표본의 갯수가 충분하지 못할 때는 T-분포를 사용한다. T-분포는 표본이 충분치 못하여 정규분포를 이루지 못할 가능성이 크기 때문에, 모집단은 정규분포를 이룬다는 가정이 필요하다. 이 가정이 있기 때문에 평균0, 분산>1 인 정규분포를 따른다.

식을 보면 다음과 같다
[Z분포]

[T분포]

[ X = 측정치, μ = 평균, σ(s)/(√n) = 표준오차, n-1=자유도 ]

두 분포의 공식을 보면 자유도 n과 n-1를 제외하고는 식이 동일하다. 즉, n이 무한으로 커지게 되면 두 분포는 동일한 분포가 됨을 알 수 있다.

---

💡 T-test

• 모집단의 표준 편차가 알려지지 않았을 때, 정규분포의 모집단에서 모은 표본(샘플)의 평균값에 대한 가설 검정이다.
  즉, T-검정은 두 집단 간 평균을 비교하는 모수적 통계방법이고, 표본이 정규성, 등분산성, 독립성을 만족 할 경우에 적용 가능하다.

모수적 & 비모수적 검정

° 모수적 검정 : 모집단의 특성을 가정하여 유도된 검정법
° 비모수적 검정 : 모집단의 모수에 대한 가정 없이 유도된 검정 → 결국 모집단이 특정 확률 분포를 따른다는 가정을 전제하지 않는다는 것이다. 비모수적 방법은 특히 categorical data(범주형 데이터)를 위한 모델링이다.

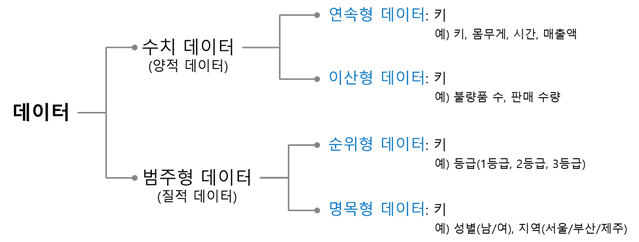
✍️ T-test의 조건

• 정규성 : 데이터의 분포가 정규분포를 따르는가?
• 독립성 : 두 데이터 그룹이 독립적인 집단인가? (한 집단이 다른 집단의 영향을 미치지 않는지)
• 등분산성 : 두 데이터 그룹의 분산이 같다고 볼 수 있는가?
  ( var.teat(a,b) 의 p-value < 0.05 : 등분산성 없다. / var.test의 H0=등분산성 있다. )

✍️ One-sample T-test

한마디로 모수의 평균(알려진 값)이랑 같은가를 검정하는 것
H0 : 모수의 평균 = 표본의 평균
H1 : 모수의 평균 != 표본의 평균

📖 Python

from scipy import stats

stats.ttest_1samp( data, 비교하려는 값 = 모수의 평균 )

✍️ two-sample T-test

두 표본 사이의 평균이 차이가 없다/있다를 검정하는 것
H0 : μ1 = μ2
H1 : μ1 != μ2

📖 Python

from scipy import stats

stats.ttest_ind( data1, data2 )

(참고)
Two-sample one-tailed test(독립표본 단측검정) : 두 샘플 중 a는 b보다 크다/작다.
Two-sample two-tailed test(독립표본 양측검정) : 두 샘플 중 a는 b보다 같다/같지 않다.


⚫ ttest_ind의 parameter. 
   alternative = 'greater/less'

'greater' 로 설정 시 
H1 = 'data1 이 data2 보다 크다'
H0 = '두 데이터 평균 차이는 유의하지 않다'

'less' 로 설정 시 
H1 = 'data2 가 data1 보다 크다'
H0 = '두 데이터 평균 차이는 유의하지 않다'