의사결정 트리는 학습 데이터에 overfitting 하는 경향이 있다. 이 한계를 극복하기 위한 방법 중 하나로 랜덤 포레스트를 적용시킬 수 있다.
💡 랜덤 포레스트(Random-Forests)
랜덤 포레스트는 앙상블(Ensemble) 방법의 머신러닝 모델이다. 앙상블이란 단어 그대로 여러 단순한 모델을 결합해서 정확한 모델을 만드는 방법이다. 즉, 랜덤 포레스트 모델은 결정트리(Decision Tree)를 여러개 만들고, 그 결과를 종합적으로 고려하여 더욱 훌륭한 모델을 만드는 것이라 할 수 있다.
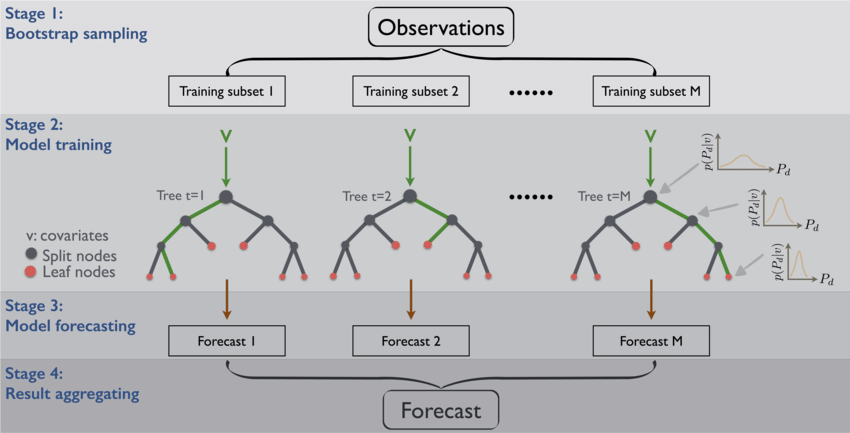
아래 그림을 통행 기본 결정트리가 어떻게 만들어 지는지 확인 해보자.
✍️ 배깅(Bagging, Bootstrap Aggregation)
먼저 부트스트랩(Bootstrap)의 개념을 알아야 한다.
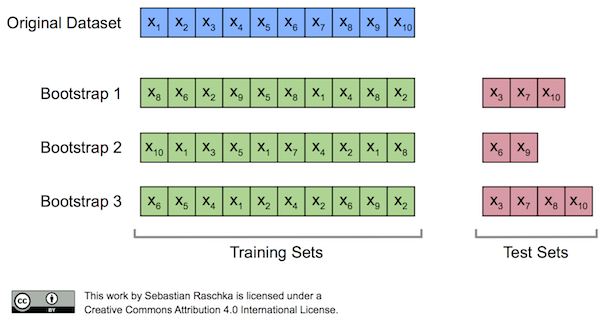
부트스트랩은 일종의 샘플링 방법이다. 아래 그림처럼 기존 데이터셋과 같은 크기의 Bootstrap subset을 복원추출(중복 허용 추출법)을 통해 샘플링 한다. 이를 Training set으로 사용하고, 추출되지 않은 데이터를 validation set으로 사용해서 검증을 거치는 여러 개의 결정트리 모델을 만드는 것이다.
이때 주의할 점은 결정 트리가 큰 트리 하나를 만드는 것이 아니라 여러 개의 작은 트리를 만들어서 숲을 이룬다는 것이다. 작은 트리라 함은 노드가 작다는 뜻인데, 이 말은 즉, feature가 작다는 뜻과 같다. 결국 raw data의 모든 feature를 사용하는 것이 아닌 Random으로 뽑은 몇 개의 feature로 결정 트리를 만든다는 것이다.
(참고로 feature는 전체 특성의 갯수가 n 이라면 개의 feature를 랜덤으로 선택한다.)
결론적으로 부트스트랩을 통해 샘플 데이터와 Feature가 랜덤으로 선택 되고, 이러한 랜덤성 때문에 의사결정 모델에 비해 랜덤 포레스트가 과적합에 강하다는 것을 알 수 있다.
이렇게 부트스트랩을 통해 만들어진 기본 결정트리 모델들을 합치는 과정을 Aggregation 이라고 한다.
- 회귀 문제일 경우 기본 모델 결과들의 평균으로 결과를 내고
- 분류 문제일 경우 다수결로 가장 많은 모델들이 선택한 것으로 결과를 낸다.
이 전체 과정을 배깅(Bagging, Bootstrap Aggregating)이라고 한다.
✍️ OOB(Out-of-bag)
부트스트랩을 통해 training set을 추출 할 때, 복원 추출을 하기 때문에 선택되지 않은 데이터가 발생한다. 이런 데이터들을 Out-of-bag 이라고 한다. (위 그림에서 Test-sets을 의미함)
부트스트랩 크기가 n개라고 가정했을 때, 그 중 하나의 샘플이 뽑히지 않을 확률은 이다.
이를 n회 복원 추출을 진행 했을 경우 그 샘플이 뽑히지 않을 확률은 이다.
결국 n을 무한히 해서, 데이터가 충분히 크다고 가정하면 0.368의 값이 나온다.
이 말은 데이터가 충분히 클 때, 어떠한 샘플이 추출되지 않을 확률이 36.8% 인 것이다.
즉, 36.8% 정도가 OOB 샘플이 되는 것이며, 이 데이터들을 기준 모델에 대입해서 검정해볼 수 있게 된다.
sklearn에서는 oob_score_ 속성을 통해 알 수 있으며, oob_score_를 보고 하이퍼파라미터를 튜닝하면서 모델 일반화를 할 수 있다.
이 전체 과정들은 statQuest youtube를 통해서 시각적으로 확인할 수 있으니 참고하면 좋다.
✍️ 특성 중요도(variable importance)
랜덤 포레스트에서는 학습 후 특성들의 중요도 정보(Gini importance)를 기본으로 제공한다.
중요도는 노드들의 지니 불순도(Gini impurity)를 가지고 계산하는데, 노드가 중요할 수록 불순도가 크게 감소한다는 사실을 이용한다. ( 즉, 노드는 한 특성의 값을 기준으로 분리가 되기 때문에, 불순도를 크게 감소하는데 많이 사용된 특성이 중요도가 올라가게 된다. )
sklearn에서 feature_importance_ 속성을 통해 확인 할 수 있다.
📖 Python
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators = 100)
# 다른 모델처럼 fit, predict를 사용한다
'''
하이퍼파라미터
n_estimators : 결정 트리의 갯수 지정. default=10.
트리 갯수를 늘리면 성능은 좋아질 수 있으나 시간이 오래 걸림
max_features : 최적의 분할을 위해 고려할 최대 feature 갯수. default=10
max_leaf_nodes : leaf node 최대 갯수
과적합을 방지할 수 있는 파라미터
min_samples_split
min_samples_leaf
max_depth
'''