✍️ 파이프라인(Pipeline)

머신러닝 프로세스에서 진행했던 결측치 처리, 스케일링, 모델학습 등 과정을 간결화 해주는 것이 바로 파이프라인이다. 코드가 단순화되니 가독성이 좋아지고, 실수가 적어진다.

파이프라인을 이용하면 여러 ML 모델을 같은 전처리 프로세스에 연결시킬 수 있다. 또한 그리드서치를 통해 여러 하이퍼 파라미터를 쉽게 연결 가능하다.

📖 Python

from category_encoders import OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline

enc = OneHotEncoder()
X_train_enc= enc.fit_transform(X_train)
X_val_enc = enc.transform(X_val)

imp_mean = SimpleImputer()
X_train_imp = imp_mean.fit_transform(X_train_enc)
X_val_imp = imp_mean.transform(X_val_enc)

scaler = StandardScaler()
X_train_sca = scaler.fit_transform(X_train_imp)
X_val_sca = scaler.transform(X_val_imp)

model_lr = LogisticRegression(n_jobs=-1)
model_lr.fit(X_train_sca, y_train)

# 파이프라인을 사용하지 않으면 위와 같이 각 과정을 적용시켜야 한다.

# 파이프라인을 사용하면 똑같은 코드를 아래와 같이 간결하게 코드를 작성할 수 있다.

pipe = make_pipeline(
    OneHotEncoder(), 
    SimpleImputer(), 
    StandardScaler(), 
    LogisticRegression(n_jobs=-1)
)
pipe.fit(X_train, y_train)

# 파이프라인의 각 단계에 접근하는 방법은 'named_steps'을 사용한다.

encoder = pipe.named_steps['onehotencoding']
imputer = pipe.named_steps['simpleimputer']
scaler = pipe.named_steps['standardscaler']
model_lr = pipe.named_steps['logisticregression']

---

💡 결정 트리(decision tree)

• 결정트리는 분류와 회귀 모두 가능한 지도학습 모델이다.
  Yes/No 질문을 이어가면서 학습을 하며, 특성에 따라 데이터를 분할해 나가는 알고리즘이다.

결정트리는 각 노드(node)로 구성되어 있고, 뿌리(root)노드, 중간(internal)노드, 말단(leaf, terminal)노드로 나눌 수 있다. 아래 그림과 같이 분류 과정을 트리 구조로 직관적인 확인이 가능하다는 장점이 있다.

이렇게 노드를 나누는 기준은 불순도(Impurity)이다. 불순도란 해당 범주 안에 서로 다른 데이터가 얼마나 섞여 있는가를 의미한다. 결정트리는 결국 Leaf Node가 가장 섞이지 않은 상태로 완전히 분류되는 되도록 하는, 즉 복잡성(entropy)이 낮도록 만들어야 한다.

불순도를 수치적으로 나타내는 척도에는 대표적으로 지니(Gini)와 엔트로피(Entropy)가 있다. 트리모델에서는 이를 비용함수(cost function)라고 하며, 노드를 분할하는 시점에 비용함수를 최소화 하는 분할 특성을 찾아내야 한다.

지니 불순도(Gini Impurity, Gini Index)

$I_G(p)=\displaystyle\sum_{i=1}^{J}p_i{(1-p_i)} = 1 - \displaystyle\sum_{i=1}^{J}p_i^2$

지니계수의 최대 값은 0.5이다.

엔트로피(Entropy)

$I_H(p) = I_E(p_1, p_2, ...,p_J) = -\displaystyle\sum_{i=1}^{J}p_i(log_2p_i)$

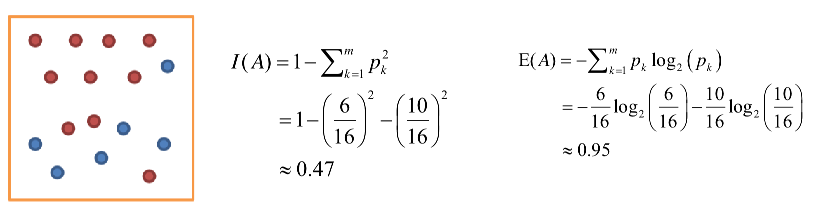
위 그림 예제는 불순도가 굉장히 높게 나온다. 불순도는 낮은 방향으로 트리를 형성해야 한다.

분기 기준 설정 시에는 부모 노드의 불순도에 비해 자식 노드 불순도가 낮도록 설정해야하며, 부모 노드와 자식 노드의 불순도 차이를 information Gain(정보 획득)이라고 한다.

지니와 엔트로피의 차이를 잘 설명해주는 블로그

결정 트리의 치명적인 단점은 트리를 계속 세분화 하다보니 과적합되기가 쉽다는 것이다.
이는 하이퍼 파라미터를 통해 조정하면서 모델을 다시 돌려보는 것이 좋다.
max_depth을 줄이고, min_samples_leaf, min_samples_split을 높여서 과적합을 조절 할 수 있다.

• min_samples_split : 노드를 분할하기 위한 최소 샘플 데이터의 수
• min_samples_leaf : leaf node가 필요로 하는 최소 샘플 데이터의 수
• max_depth : 트리의 최대 깊이

DecisionTreeClassifier 공식문서

참고로 사이키런의 DicisionTreeClassifier를 통해 분류를, DicisionTreeRegressor를 통해 회귀 모델을 만들 수 있다.

📖 Python

from category_encoders import OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.tree import DecisionTreeClassifier
from sklearn.pipeline import make_pipeline


pipe = make_pipeline(
    OneHotEncoder(use_cat_names=True), 
    SimpleImputer(), 
    DecisionTreeClassifier(min_samples_leaf=10, random_state=2))

pipe.fit(X_train, y_train)

# 정확도 구하기
pipe.score(X_train, y_train)

결정 트리모델 시각화

# graphviz 설치: conda install -c conda-forge python-graphviz

import graphviz
from sklearn.tree import export_graphviz

model_dt = pipe.named_steps['decisiontreeclassifier']
enc = pipe.named_steps['onehotencoder']
encoded_columns = enc.transform(X_train).columns

dot_data = export_graphviz(model_dt
                          , max_depth=3
                          , feature_names=encoded_columns
                          , class_names=['no', 'yes']
                          , filled=True
                          , proportion=True)

display(graphviz.Source(dot_data))

---

✍️ 특성중요도(feature importances)

선형모델에서는 feature와 target의 관계를 회귀 계수(coefficients)를 통해 확인했다. 결정 트리 모델에서는 그 역할을 특성중요도가 하게된다.
특성중요도는 항상 양수 값을 가지게 되며, 모든 특성들의 중요도를 합하면 1이 된다.
특성중요도가 높은 feature일수록 노드를 나눌 때 먼저, 그리고 자주 사용된다는 것을 알 수 있다.

📖 Python

model_dt = pipe.named_steps['decisiontreeclassifier']
enc = pipe.named_steps['onehotencoder']
encoded_columns = enc.transform(X_trian).columns

# 특성 중요도를 DF으로 표현
importances = pd.DataFrame({'feature' : encoded_columns,
                            'importances' : model_dt.feature_importances_})

# 내림차순 정렬
importances.sort_values('importances', ascending = False)

# 시각화하여 bar plot으로 나타내면 더욱 확인하기가 쉽다.

---