💡 Ridge Regression

릿지 회귀는 기존 선형 회귀(Linear Rigression)의 과적합을 해소해주는 선형회귀 방법이다.
즉, 편향을 조금 높이는 대신 분산을 줄이는 방법으로 정규화를 수행하는 것이다. 여기서 말하는 정규화는 모델을 변형하여 과적합을 완화해 일반화 성능을 높여주는 것을 말한다.

기존의 선형 회귀 모델은 OLS(최소제곱법)에서 잔차의 합(RSS)가 최소가 되는 것을 선택했다.
Ridge 회귀 식을 보면 RSS 에 λ*(회귀계수의 제곱 합)을 더해주는데, 이때 λ 는 패널티로 작용하게 된다.

• Ridge Regression의 식
  $β_{ridge} = argmin[\textstyle\sum_{i=1}^{n}{(y_i-β_0-β_1x_1 -...-β_nx_{in})^2} + λ\textstyle\sum_{j=1}^{p}{(β_j^2)}] \\$

$=RSS + λ\textstyle\sum_{j=1}^{p}{(β_j^2)}$

( n: 샘플수, p: 특성수, : 튜닝 파라미터 )

아래 그림에 대한 상세한 설명은 블로그 의 글을 통해 자세하게 확인 할 수 있다.

---

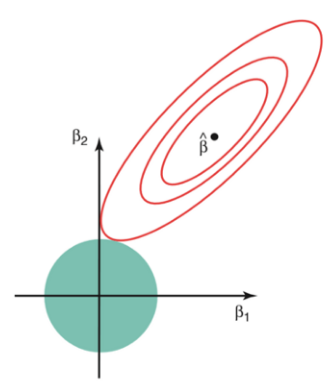
⭐ λ (람다, lambda, alpha, penalty) ?

• 람다란 패널티(즉, 규제)의 개념이다.
• λ = 0이면 RSS만 최소화 하기 때문에, 기존 선형 회귀 모델과 같아진다.
  λ 값이 커질수록 회귀계수는 0에 수렴하게 되고 기울기가 점점 완만해진다. ( 0<λ<$∞$ ) 이는 종속 변수가 독립 변수의 변화에 따른 변화가 민감하지 않다는 의미로 이상치에 덜 민감하다고 할 수 있다.
• 단, λ 값이 너무 커질 경우, 잔차가 커져서 편향이 커지게 되기 때문에 최적의 λ 값을 찾는 것이 중요하다.

---

📖 Python

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge

# 데이터셋 load
df = sns.load_dataset('anscombe').query('dataset=="III"')

# λ 값을 변화 시키면서 회귀 계수의 변화를 확인
def ridge_ans(alpha):
    ridge = Ridge(alpha=alpha, normalize=True)
    ridge.fit(df[['x']], df['y'])
    
    df['y_pred'] = ridge.predict(df[['x']])
    
    #시각화 표현
    m = ridge.coef_[0].round(2)
    b = ridge.intercept_.round(2)
    title = f'alpha={alpha} \n y = {m}x + {b}'
    
    ax = df.plot.scatter('x', 'y', c='black')
    df.plot('x', 'y_pred', ax=ax, c='r', title=title)

    plt.show()
    
    
alphas = np.arange(0, 2.1, 0.4)
for alpha in alphas:
    ridge_ans(alpha=alpha)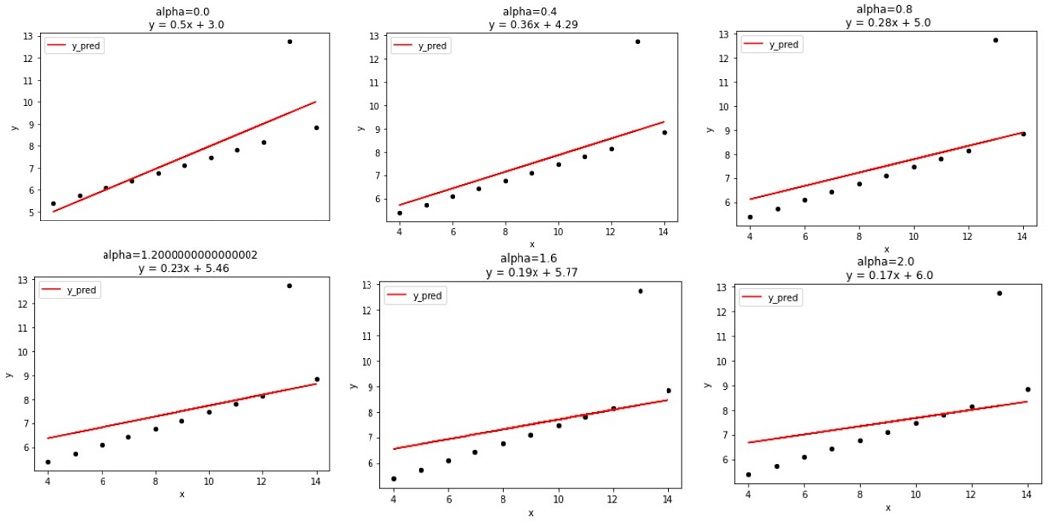

---

λ의 값이 커질 수록 기울기가 완만해지고, 회귀계수가 줄어드는 것을 볼 수 있다. λ를 통해 편향을 높이고 분산을 줄이면서 train data에 과적합 되지 않도록 조정을 한 것이다.

그렇다면 어떤 λ의 값이 최적의 값인지 알 수 있는 방법은 무엇일까?
매번 위의 for문을 통해 λ 값을 얻기는 힘들기 때문에 최적의 λ 값을 찾아주는 함수를 이용할 수 있다.

💡 RidgeCV

RidgeCV는 최적의 λ 값을 찾고, CV라는 parameter를 통해 교차 검증을 진행하게 된다.
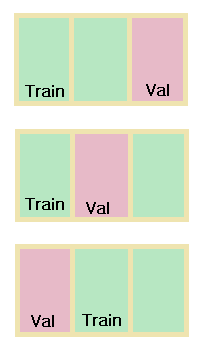
CV (Cross validation)는 K-fold 교차 검증이다. 만약 cv=3으로 준 경우, 아래 그림처럼 데이터를 자체적으로 3개로 나눠서, train data와 validation data로 자체적인 검증을 통해 정확도를 높여주는 것이다.

📖 Python

from sklearn.linear_model import RidgeCV

alphas = np.arange(1, 10, 0.2)

# RidgeCV model. cv=2, λ=1~10

#train data로 모델 학습 후 test data로 predict
model = RidgeCV(alphas = alphas, cv = 2) 
model.fit(X_train, y_train)
y_pred = model1.predict(X_test)

# MAE, R2 확인
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'Test MAE: ${mae:,.0f}')
print(f'R2 Score: {r2:,.4f}\n')

# 최적의 λ와 score 확인
print(f'alpha: {model.named_steps["ridgecv"].alpha_}')
print(f'cv best score: {model.named_steps["ridgecv"].best_score_}')


# 최종모델
X_total = pd.concat([X_train, X_test])
y_total = pd.concat([y_train, y_test])

model = RidgeCVRegression(alphas=alphas, normalize=True, cv=5)
model.fit(X_total, y_total)