지도학습의 회귀와 분류에 있어서는 서로 다른 모델을 선택해야한다. 전까지 배운 내용이 회귀모델에 대한 내용이었다면, 오늘은 분류 알고리즘의 하나인 로지스틱 회귀에 대해 공부해 보자.

---

💡로지스틱 회귀(Logistic Regression)

로지스틱 회귀는 사건의 발생 가능성을 예측하며, 종속 변수가 범주형일 때 사용하는 예측 모델이다.

아래 그림을 보면 선형 회귀 모델은 독립 변수의 값이 증가할수록 종속 변수의 값도 증가/감소 하는 형태를 가진다. 반면에 로지스틱 회귀 모델은 독립변수 값이 아무리 크게 변해도 종속 변수는 0과 1사이의 값으로 나타나는 것을 알 수 있다.

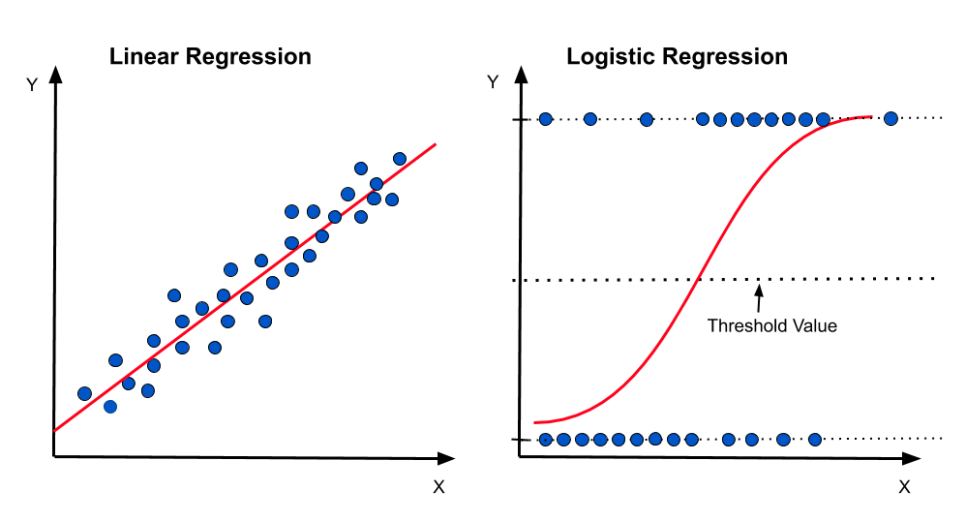
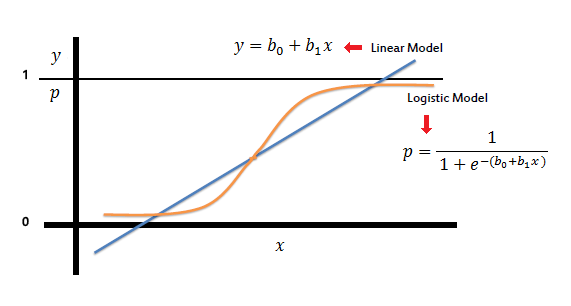
아래 그림의 식을 보면 로지스틱 모델의 식이 선형 회귀 모델 식을 포함하고 있다. 즉, 선형 모델을 시그모이드 함수와 결합하고고, 이를 통해 분류 문제를 해결한다고 보면 된다.

그러나 분류 모델에서는 선형 모델과 달리 회귀 계수를 통한 직관적 해석이 어려운데, 이때 사용하는 개념이 바로 오즈(Odds)와 로짓변환이다.

---

⭐ 오즈(Odds)

오즈는 실패확률에 대한 성공확률의 비를 말한다. (P = 성공확률, 1-P = 실패확률)
즉, Odds = 3이라면 성공확률이 실패확률의 3배라는 뜻이다.

• $Odds =$ $\frac{P}{1-P}$

  $P=1 \rarr Odds = \infin$
  $P= 0 \rarr Odds = 0$
  

로지스틱 회귀 함수를 $Odds$에 대입하면 다음과 같은 식이 나온다.

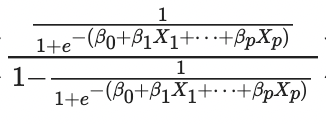
로지스틱 회귀는 비선형 함수라 회귀 계수의 의미를 해석하기가 어렵다. 이 때 로짓 변환을 통해 비선형 형태인 로지스틱 함수 형태를 선형 형태로 만들어 회귀 계수의 의미를 해석하기 쉽게 할 수 있다. 즉, $X$의 증가/감소에 따라 로짓($In(Odds)$)이 얼마나 증가/감소했다고 해석 할 수 있다.

---

⭐ 로짓 변환(Logit transformation)

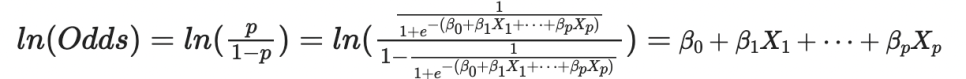
로짓은 오즈에 로그를 씌운 값($In(Odds)$)이다.
이렇게 오즈에 로그를 씌어 변환하는 과정을 로짓 변환이라고 한다. 위 식을 보면 결국 로짓 변환을 통해 선형의 식을 도출해내고, 독립 변수 $X$에 따른 로짓의 변화를 알 수 있게 된다.

참고로, 왜 오즈에 로그를 씌워 $logit$을 사용하는지는 여기서 쉽게 설명해준다.

---

머신 러닝 모델을 만들고 나면, 모델의 예측력을 평가 해봐야한다. 회귀 모델에서는 $MAE, MSE, R^2$와 같은 평가 지표를 이용했었는데, 분류 모델에서는 분류 모델만의 평가 지표가 따로 있다.
여러 가지가 있지만 여기서는 Accuracy(정확도)에 대해서만 다뤄보자.

우선 내용을 알기 전에 오류에 대해 알아야한다. 예전에 가설 검정하는 부분에서 다룬 적이 있는데, 바로 1종오류와 2종오류에 대한 내용이다.

다시 정리해보자면 다음과 같다.

True Positive: 실제 Positive인 정답을 Positive라고 예측 (True)
True Negative: 실제 Negative인 정답을 Negative라고 예측 (True)
False Positive: 실제 Negative인 정답을 Positive라고 예측 (False) – Type I error
False Negative: 실제 Positive인 정답을 Negative라고 예측 (False) – Type II error

⭐ Accuracy(정확도) : 분류 모델의 평가 지표

• $Accuracy = \frac{TP + TN}{TP+TN+FP+FN}$

정확도는 전체 예측 건수에서 정답을 맞친 건수의 비율이다.
이때 정답을 맞췄다는 것은 Positive 인지 Negative인지랑은 관계없이 True인 것을 말한다.

이러한 전체 내용을 Python의 Sklearn Lib를 통해서 간단하게 구현 가능하다.

📖 Python

# 로지스틱 회귀모델
from sklearn.linear_model import LogisticRegression

logistic = LogisticRegression()  # 인스턴스
logistic.fit(X_trian, y_train)   # 모델 학습
logistic.predict(X_test)         # 예측

logistic.score(X_train, y_train) # train set의 정확도


# 정확도
from sklearn.metrics import accuracy_score

accuracy_score(y_train, y_pred)


# 오늘 배운 새로운 함수 : SimpleImputer
# 결측치 default
from sklearn.impute import SimpleImputer

imputer = SimpleImputer()
imputer.fit_transform(X_train)  # X_train set의 결측치를 mean으로 채움.

SimpleImputer 공식문서