💡 선형회귀

머신러닝의 목적은 데이터의 알려진 속성들을 학습하여 예측 모델을 만드는데 있다. 이때 찾아 낼 수 있는 가장 직관적이고 간단한 모델은 선(line)이다. 선형회귀란 데이터를 가장 잘 대변하는 최적의 선을 찾은 과정이다.
아래 그래프에서 검정색 점이 데이터이다. 이 데이터를 가장 잘 표현하는 선이 파란색 직선이며, 이는 일차 함수($y=ax+b$) 형태로 나타난다.

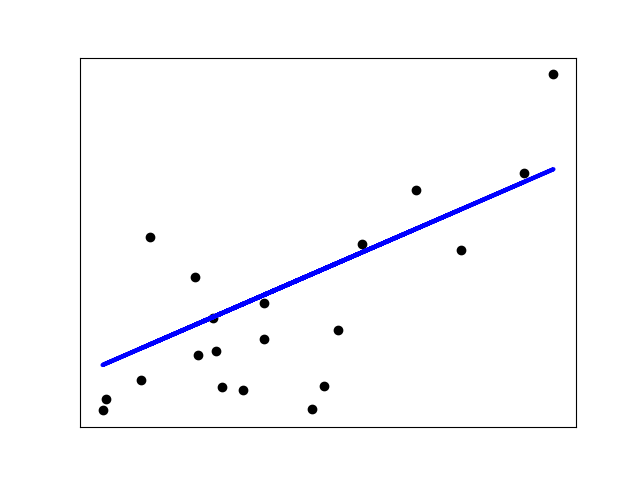
선형회귀 직선은 $x$와 $y$의 관계를 요약해서 설명해준다고 볼 수 있다.
이 때 $x$를 독립 변수라고 하며, $x$에 의해 영향을 받는 값인 $y$를 종속 변수라고 한다.
선형 회귀는 한개 이상의 독립 변수 $x$와 $y$의 관계를 모델링 하는데, 만약 독립 변수 $x$가 하나라면 단순 선형 회귀, 2개 이상이면 다중 선형 회귀라고 한다.

• 독립 변수는 예측(Predictor)변수, 설명(Explanatory), 특성(Feature) 등으로 불린다.
• 종속 변수는 반응(Response)변수, 레이블(Label), 타겟(Target) 등으로 불린다.

• 단순 선형 회귀 분석 : $y = β_1x + β_0$
• 다중 선형 회귀 분석 : $y = β_0+β_1x_1 + β_2x_2 + ...w_nx_n$

---

공부시간에 따른 시험 점수를 나타낸 표가 있다. 알고있는 데이터로부터 $x$와 $y$의 관계를 유추하고, 표에 없는 10시간 공부하였을 때 성적을 예측하고자 한다. 머신러닝에서는 $x$와 $y$의 관계를 유추하기 위해 식을 세우게 되는데 이것을 가설($H$)이라고 한다.

---

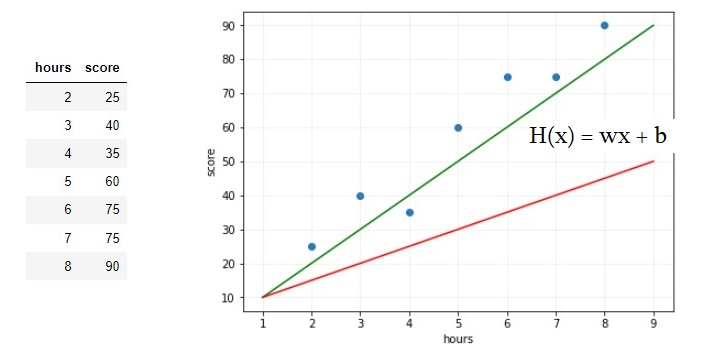
💡 기준모델 & 예측모델

• 기준 모델 : 예측 모델을 구체적으로 만들기 전에 가장 간단하면서도 직관적으로 최소한의 성능을 나타내는 기준이 되는 모델이다.
  대표적으로 분류와 회귀에서는 각각 최빈값과 평균값을 사용한다.
  분류 : 최빈값
  회귀 : 평균값
  시계열회귀문제 : 이전 타임스탬프의 값

📖 Python

'''
GrLivAre(지상 생활면적)에 따른 SalePrice(주택 판매 가격)을 예측
'''
# predict: 개발자가 정한 기준모델인 평균으로 예측
predict = df['SalePrice'].mean()

x = df['GrLivArea']
y = df['SalePrice']

predict = df['SalePrice'].mean()
errors = predict - df['SalePrice']
mean_absolute_error = errors.abs().mean()   # 기준모델로 예측한 절대평균에러 값

# 시각화
sns.lineplot(x=x, y=predict, color='red')  # 기준모델
sns.scatterplot(x=x, y=y, color='blue');   # 전체 데이터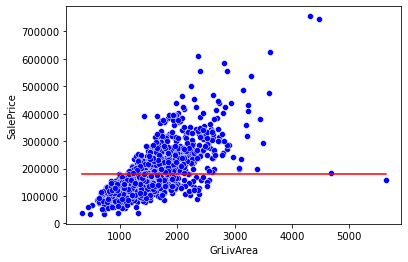

기준 모델의 절대평균 에러 값(A)과 예측 모델의 에러 값(B)을 비교해서
A > B 이면, 예측 모델의 성능이 기준 모델보다 좋다고 판단한다.

• 예측 모델
  ⭐최소자승법(Ordinary Least Square, OLS)
  : 위의 scatter plot에 Best fit Line을 그리면, 그것이 회귀 예측 모델이 된다. 이 회귀 직선을 그리기 위해서는 최소자승법(=최소제곱법)을 이용해야 한다.
  최소자승법은 잔차제곱의 합(RRS, residual sum of squares)를 최소화하는 가중치 벡터를 구하는 방법이다.
  선형 회귀식 : $y = α + βX$ (α=y절편(intercept), β=회귀계수(Coefficients))

💭 잔차란 예측값과 관측값의 차이이다. 잔차 제곱의 합을 RSS 혹은 SSE(Sum of Square Error)라고도 하며, 이 값이 회귀모델의 비용 함수(Cost function)이 된다. 머신러닝에서 이 Cost Function을 최소화 하는 모델을 찾는 과정을 학습이라고 한다.

---

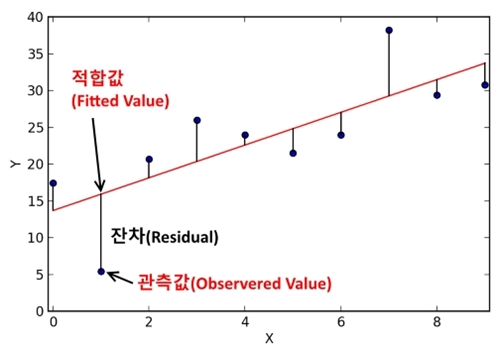
[참고: 자주 잊어서 적어놓는 내용]

$MAE= \frac{1}{n} \displaystyle\sum_{i=0}^{n}{\vert \hat{Y_i}-Y_i \vert}\\$

$MSE= \frac{1}{n} \displaystyle\sum_{i=0}^{n}{(\hat{Y_i}-Y_i)^2}\\$

$RMSE = \sqrt MSE$

---

📖 Python

OLS를 활용한 Linear Regression

from sklearn.linear_model import LinearRegression

model = LinearRegression()  # 예측모델 인스턴스 만들기
model.fit(X, Y)   # 모델 학습(fit)하기
model.predict(new data)   # 새로운 데이터 예측하기
'''
sklearn 을 통해 모델을 만들고 데이터를 분석하기 위해서는 데이터 구조가 정해져 있다.
(아래 그림 참고)
* feature data와 target data를 나누어 준다.
* feature data는 주로 X 로 표현. 보통 2차원 행렬 ([n_samples, n_features])
(주로 numpy 행렬이나 pandas DataFrame으로 표현)
* target data는 주로 y로 표현. 보통 1차원 형태 (n_samples)
(주로 numpy 배열이나 pandas series로 표현)
'''

#[예시] : GrLivArea에 따른 SalePrice를 예측하는 모델

model = LinearRegression()

# X : feature data, y : target data 만들기
feature = ['GrLivArea']     # 행렬의 형태라 [[]]
target = ['SalePrice']
X_train = df[feature]
y_train = df[target]

model.fit(X_train, y_train)

# 새로운 데이터 샘플로 학습한 모델을 통해 예측하기
# GrLivArea = 4000 일때 예상 SalePrice는?
X_test = [[4000]]
y_test = model.predict(X_test)    # 예측가격 : $447090 

'''
# 참고
X-Train 값의 범위 내에 존재하지 않는 독립변수를 넣어서 예측하는 경우를 보간(Interpolate)
범위를 넘어서는 값을 넣어서 종속변수를 예측하는 경우는 외삽(Extrapolate)이라고 한다.
'''

[sklearn 사용 시 데이터 구조]

---

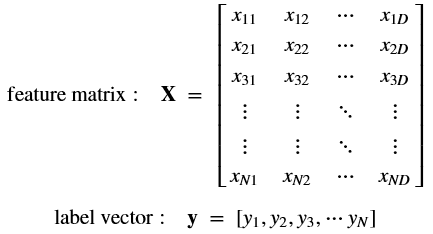
✍️ 선형 회귀 모델의 계수(Coefficients)

학습한 모델을 통해 종속 변수 값을 알 수 있지만, 회귀 계수와 절편을 값을 각각 구하는 방법도 있다.

$y=αx_i+β$

(회귀 계수 : α, 절편 : β)

# 회귀 계수(coefficient)
model.coef_

# 절편(intercept)
model.intercept_

---