머신러닝 모델을 학습하고 평가하기 위해서는 Dataset을 3가지로 분류한다.
- Train set
- Validation set
- Test set
이 데이터는 일반적으로 Train : Validation : Test = 6 : 2 : 2 로 이용한다.
⭐ Train set
: 오로지 모델을 학습하기 위해 필요한 data set (이 때 학습은 최적의 파라미터를 찾는 것)
⭐ Validation set
: 학습이 이미 완료된 모델을 검증하기 위한 data set
-> 직접 학습을 시키진 않지만 학습에 '관여'는 함⭐ Test set
: 모델의 '최종 성능'을 평가하기 위한 data set
-> 학습에 관여하지 않음
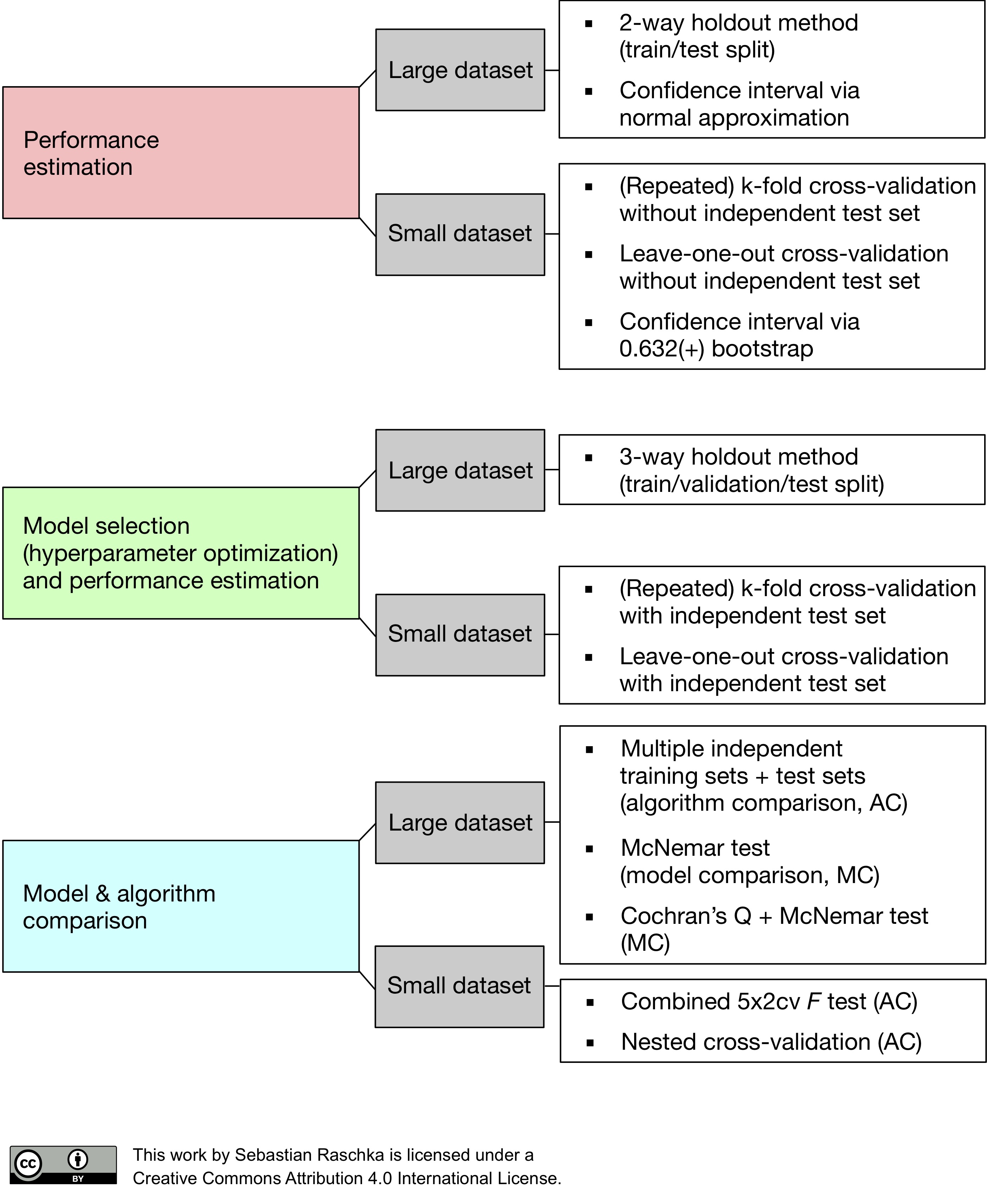
💭 데이터를 분리하는 목적
: Overfitting(과적합) 방지 & Unseen data 에 대한 좋은 성능
머신러닝 모델에 Train data를 100% 학습 시킨 후, test 데이터에 모델을 적용했을 때 성능이 나오지 않는 경우가 많다. overfitting 되었기 때문이다.
이 때 validation set으로 학습된 모델 검증 시 예측률이나 오차율이 떨어지면 과적합 되었다고 확인하고, 학습을 종료시킨다.
📖Python
# sklearn을 통해 간단하게 data set을 분리할 수 있다.
from sklearn.model_selection import train_test_split
data = dataset['data']
target = dataset['target']
# train_test_split
x_train, x_test, y_train, y_test =
train_test_split(data, target, test_size=0.2, shuffle=True, random_state=34)
'''
test_size: 테스트 셋 구성의 비율. 20%를 test(validation)셋으로 지정하겠다는 의미
shuffle: default=True. split을 해주기 이전에 섞을건지 여부
random_state: 매번 데이터셋이 변경되는 것을 방지
stratify: default=None. classification을 다룰 때 매우 중요한 옵션값.
stratify 값을 target으로 지정해주면 각각의 class 비율(ratio)을
train / validation에 유지해 줌. (한 쪽에 쏠려서 분배되는 것을 방지)
만약 이 옵션을 지정해 주지 않고 classification 문제를 다룬다면,
성능의 차이가 많이 날 수 있음
'''일반화(Generalization)
Train data를 통해 훈련한 모델이 Unseen data에 대해서도 성능 차이가 나지 않게 하는 것이다.
즉, Unseen data를 넣어도 Training data로 학습한 것과 거의 비슷한 결과를 얻는 것이며, 이를 일반화가 잘 된 모델이라고 한다.
Test data에서 만들어내는 오차를 일반화 오차라고 한다.
⭐과적합
:모델이 train data를 과하게 학습한 나머지 지나치게 복잡해져서, train data에서는 높은 성능을 보이지만 test data에서 제대로 성능을 발휘하지 못하는 문제
⭐과소적합
모델이 너무 단순해져서 train data에서도 성능을 발휘하지 못하는 문제
분산(Variance) - 편향(Bias) Trade-off
학습된 모델을 통해 얻게 되는 예측값의 동태를 분산과 편향으로 표현할 수 있다.
⭐분산(Variance)
데이터가 얼마나 퍼져있는지를 나타내는 값이다.
분산이 크다는 것은 모델이 학습 데이터의 이상치에 민감하게 반응하여 일반화를 제대로 하지 못한 상태이다. 즉, 과적합 된 모델의 경우 분산이 크다고 할 수 있다.
⭐편향(Bias)
실제 값과 예측 값이 얼마나 떨어져 있는지를 나타내는 값이다.
편향이 크다는 것은 모델이 학습 데이터에서 독립변수와 종속변수의 관계를 잘 파악하지 못한 상태란 것이다. 즉, 과소적합된 모델의 경우 편향이 크다고 할 수 있다.
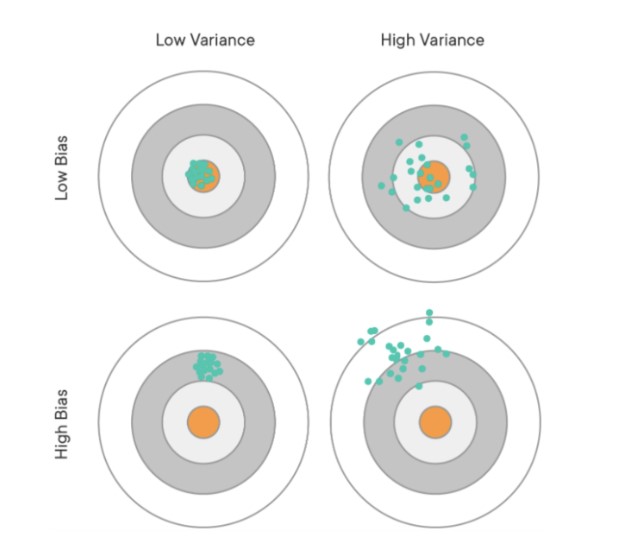
결국 편향과 분산은 Trade-off의 관계를 가진다.
과적합일 경우 : 편향 , 분산
과소적합일 경우 : 편향 , 분산
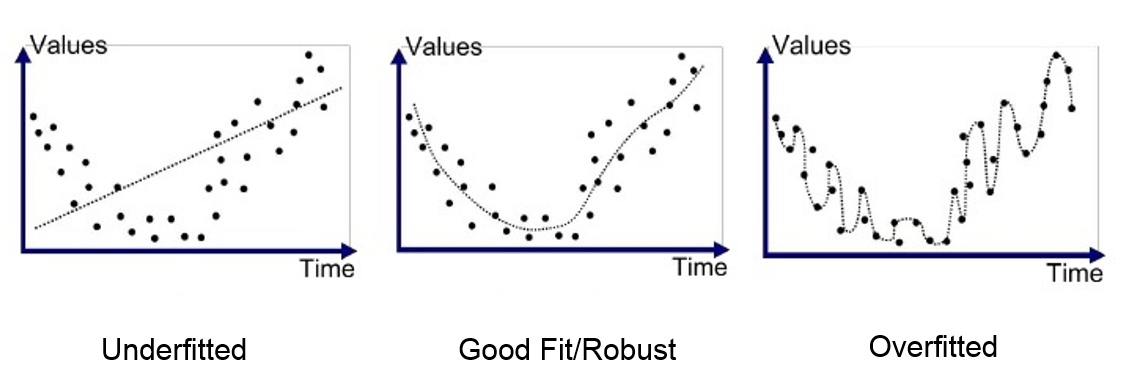
과적합된 모델은 train data를 잘 설명하므로 Bias는 적지만, test data에 대해서 성능이 떨어져 variance가 클 수 밖에 없다.
반면 과소적합된 데이터는 너무 train data에만 최적화 되어 있지 않기 때문에, test data를 넣어도 성능이 급격히 떨어질 일은 없어서 variance는 적은 반면, 기본적인 train data 조차 설명하지 못해 Bias가 클 수 밖에 없다.
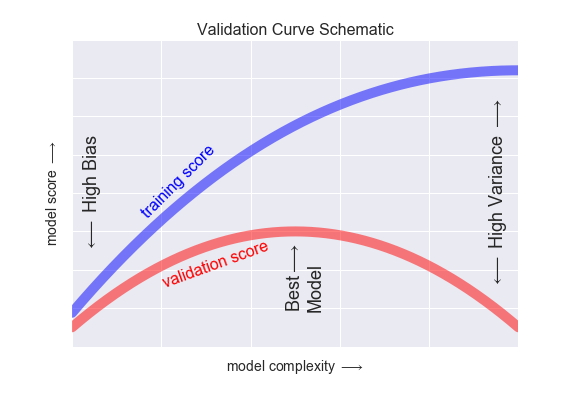
좋은 모델은 당연히 편향도 낮고 분산도 낮은 모델이다.
아래 그림에서 알 수 있듯 모델이 복잡해 질수록 train data 성능은 계속 증가하는데 test data는 어느 정도에서 멈춰 하강하게 된다. 이 시점에 과적합이 일어난다고 보는데, 그 이상 복잡한 모델은 필요치 않다고 본다.