💡 큰수의 법칙 (Law of large numbers)
- 큰 수의 법칙이란 어떤 모집단에서 표본 집단들을 추출할 때, 추출한 데이터의 크기가 커질수록
그 표본 집단들의 평균은 모평균과 같아지고, 표본 집단들의 분산은 0에 가까워진다는 것이다.
💡 중심극한정리 (Central Limit Theorem)
- 중심극한정리는 표본의 수가 충분히 많으면, 모집단의 분포 형태와 상관없이 표본평균의 분포가 정규 분포에 가까워진다는 것이다.
큰수의 법칙, 중심극한의정리 모두 표본집단의 크기가 커짐에 따라 발생하는 현상이다.
그러나 '큰수의 법칙'은 표본 크기가 무한히 커짐에 따라 표본평균이 모평균으로 "확률수렴"을 한다는 개념이고, '중심극한정리'는 표본 크기가 무한히 커짐에 따라 표준화한 표본평균의 분포가 표준정규분포로 "분포수렴"하는 개념이다.
즉, 대수의 법칙은 확률수렴 측면이고, 중심극한정리는 분포수렴 측면의 개념이다.
# 천천히 읽어보고 이해하기
확률수렴
Xn이 무한대로 증가함에 따라,
Xn과 X 차이의 절대값에 대한 확률의 극한값이 0이면 Xn이 X로 확률수렴한다고 함.
분포수렴
확률변수 X가, 극한분포가 연속인 모든 점에 대해서,
누적분포함수 Fxn의 극한값이 누적분포함수 Fx와 같다면 Xn이 X로 분포수렴한다고 함.
💡 신뢰구간
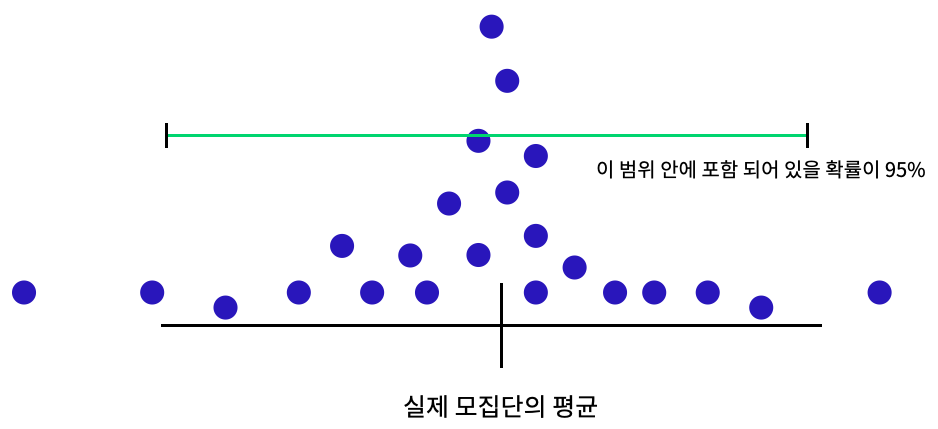
- 모수가 있을 것으로 예상되는 범위이다.
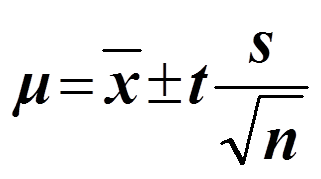
신뢰도를 95%라고 가정한다면, 신뢰구간은 아래 그림처럼 표현할 수 있다. 표본을 뽑아 평균을 내는 것을 100번 한다면 95번은 녹색 선의 범위 내에 나타낼 수 있다는 것이다.(신뢰구간)
t• 는 error, x bar는 추정 평균이다.