Linear Classification

D차원의 유클리드 벡터 x가 입력으로 있다고 가정한다. 이때 해당 벡터 x에 대해 두가지 속성으로 구분하고자 한다면 이를 Binary classification이라고 하며, 그 이상으로 구분하고자 한다면 Multi-Classificaton이라고 한다. 이 과제의 주요 목적은 구분하는 경계, 즉 Decision Boundary에 해당하는 Hyperplane을 찾는 것이라고 할 수 있다.

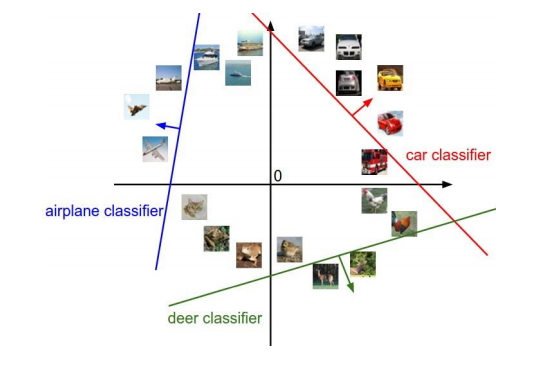
이때 출력 Y는 바이너리의 Y/N에 해당하는 클래스들로 구분이 되며 주로 0과 1 혹은 1, -1로 구분이 된다. 이러한 클래스들로 구분하기 위해서는 ML이나 MAP를 찾을 때처럼 Training Set, Validation Set, Decision Set으로 구분할 수 있으며 이때 Hypothesis class는 sign(w^Tx)이다. (이때 sign(x)는 x>=0일 때 1이고, otherwise -1의 값을 가진다.)

Linear Classification Streamline

Linear Classfiication의 Streamline은 sign(w^Tx)로 initialize를 진행한다. 다음으로 Zero-one loss, Hinge loss, Cross-entropy loss와 같은 Loss Function에 대해 오류률을 확인하여 Gradient Descent로 알고리즘을 최적화하는 것으로 정의할 수 있다. 이때 Loss Function을 이용하는 방법에 대해서는 Score과 Margin에 대한 이해가 필요하다.

Score을 활용하는 방법에 대해 정확하게 알아보자. 활용성을 알아보기 위해 뒤의 Zero-One Loss의 개념을 들고온다.

Zero-One Loss

Zero-One Loss의 존재는 매우 간단하다. 정답이면 0, 틀리면 1을 출력하는 Loss Function으로, L(y', y)=sign(y'!=y)로서 표현할 수 있다.

이 경우에 대입하면, 해당 점, 사용자가 임의로 부여한 클래스, Hyperplane의 수직벡터값인 Loss 0-1 (x, y, w)에 대해 sign(wx) != y인지 확인해서 if True return 0, otherwise return 1으로 표현할 수 있다.

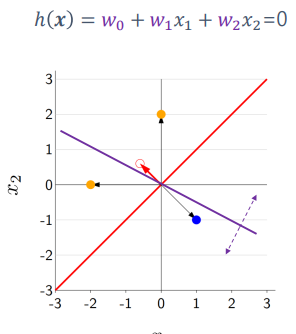
위의 그림을 예시로 들어 이를 증명하여 보자.

먼저 (0.2)에 있는 점 A를 사용하여 이를 증명한다. 주어진 식으로 이를 표현하면 아래와 같으며 Class는 1로 설정한다. 주어진 Hyperplane의 직각벡터는 (0.5,1)이게 되므로
Loss((0.2), 1, (0.5,1)) = 1sign((0.5,1)(0,2)!=1)=sign(2!=1)=0에 해당하는 것을 알수 있다.

이때 Score 값은 (w^T phi(x))으로, +1을 예측하는 데에 대한 자신을 알려주는 지표라고 보면 되고, 이에 대해 Y값을 실제로 곱해 실제로 맞는지를 확인하는 것이 바로 Margin이라고 할 수 있다.

Zero-one loss의 의미는 Loss를 최대한으로 줄이는 것인데, w에 대한 Delta Trainloss를 줄이기 위해서 Train Data에 해당하는 모든 데이터 값에 대해 Zero-one loss를 줄여야 한다.

이때 Y값이 급격하게 커지고, Positive Value를 가지는 경우 Margin의 크기가 매우 커지게 되는데 이 Margin을 얼마나 정확하게 측정하였는지에 대한 지표로서 활용한다.

Other Loss Functions

Hinge Loss

Hinge Loss는 max{1-(wphi(x)y,0}를 구하는 함수로, 아래와 같이 정의할 수 있다. 이 부분의 특징은 0-1 Loss와 상당히 유사한데, 0에 해당할 경우 -phi(x)y를 출력하고 1인 경우 0을 출력하는 것이 대표적이다.

Cross Entropy Loss

Cross Entropy Loss는 Scalar Input에 대해 Prediction y = p(C1|x)을 sigma을 통해 Class 1의 사후 확률로 사용, 이에 대한 Loss Function을 구하는 것이라고 할 수 있다.
우선 Binary Classification의 경우 Loss Function은 다음과 같은 정의가 가능하다.
E(w) = (t=1일 때 -ln y, otherwise -ln(1-y)으로 측정되는데, 이때 두 가지 클래스에 의거하여 만들어진 Cross-Entropy는 -t(lny)-(1-t)ln(1-y)로 정의할 수 있다. 또 이를 전체 데이터값에 할당하면 각 데이터들의 Cross-Entropy들의 합으로 정의내릴 수 있게 된다.
Cross Entropy는 Real Value인 w^Tphi(x)에 대해서 Sigmoid Function이라는 그래프를 통해 이를 구현해낼 수 있게 된다. 이때 주로 0.5이상의 Estimated Y에 대해 1의 출력값을 주로 보내게 된다. 물론 Gradient Descent Method에 의해 학습을 진행할 수 있고, Gradient 값과 Likelihood, Derivative, Gradient Sigmoid 및 Gradient of Cross Entropy를 구할 수 있게 된다.
Linear Classifier를 훈련시키는 방법은 Gradient Descent를 사용한 Iterative Optimization을 구현하여 나타낼 수 있다.

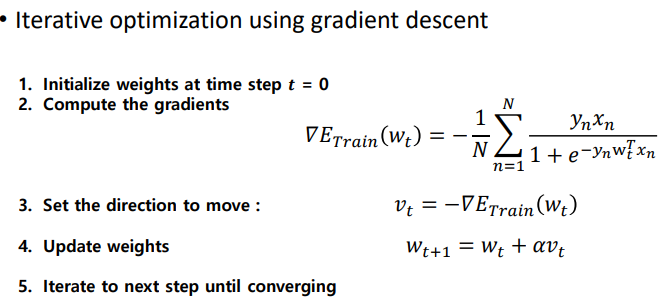
다음으로 Multiclass Classification을 구현하는 경우, 아래와 같이 행렬로 구현한다.

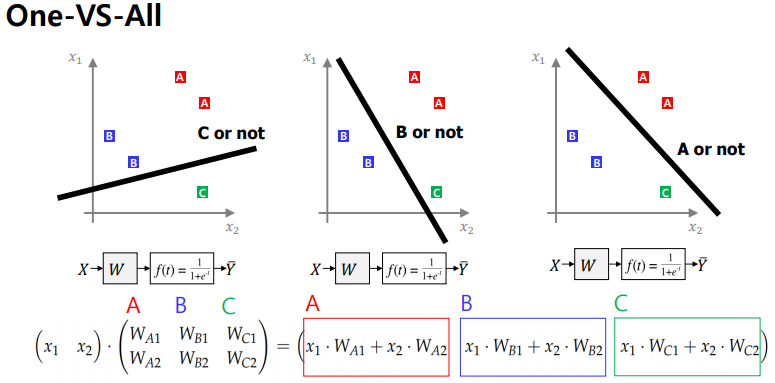
이때 One-hot Encoding을 주로 사용하게 되는데, One-hot Encoding이란 0으로 이루어진 벡터내에서 단 한개의 1의 값으로 해당 데이터의 값을 구별하는 것으로, 예를 들어 (0.1)이라고 하는 점이 A,B,C의 클래스 중 A값에 해당할 때, 해당 점의 One-hot Encoding 값은 (1, 0, 0)T가 된다.

Advantages of Linear Classification

Linear Classification이 가지는 장점은 단순성과 해석 능력이다.
우선 단순성은 말 안해도 알것이고 해석능력은 어떠한 능력 => 어떠한 결과가 눈에 선명하게 드러난다는 점이 장점이라 할 수 있다.