출처: DSBA 연구실 유튜브 와 DSBA 연구실 강의자료 를 참고하면서 스터디를 진행하였습니다.

주제: Anomaly Detection: (Mixture of) Gaussian Density Edstimation

---

1. Density-based Novelty Detection

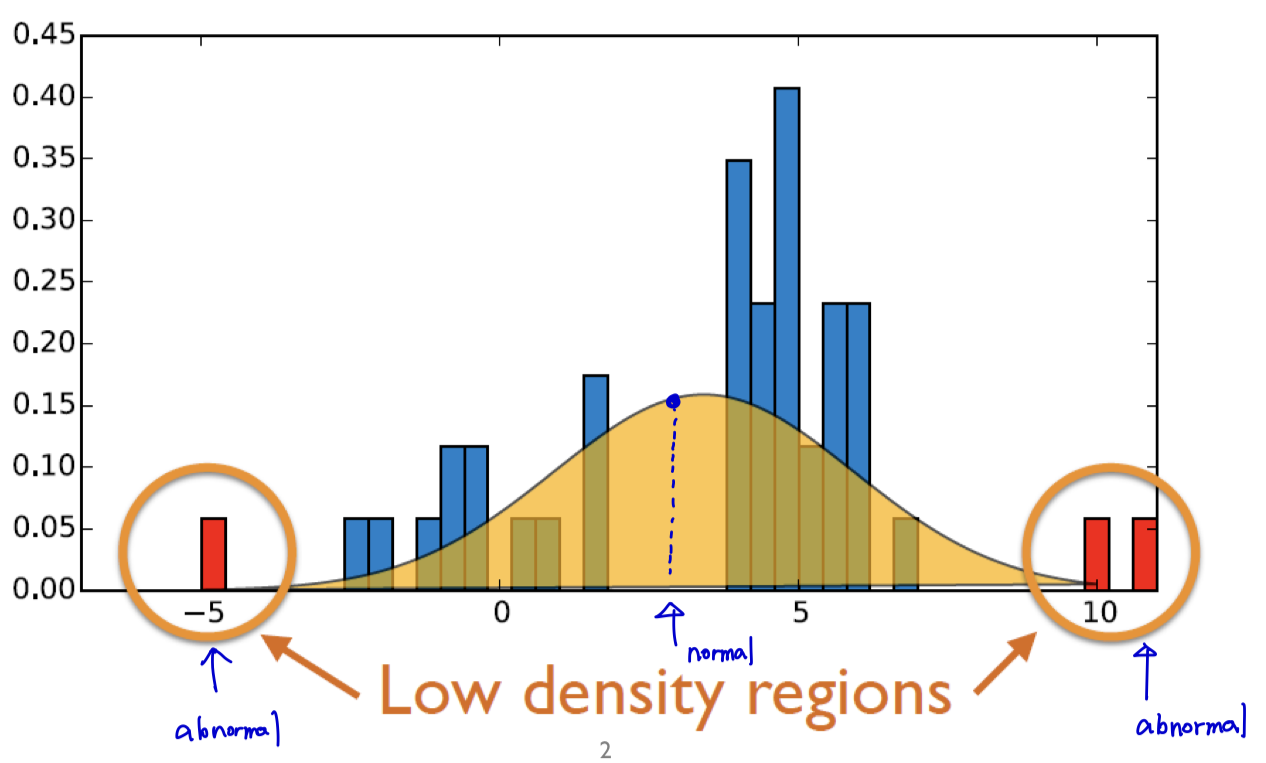
• 주어진 데이터를 활용해서 정상적인 normal 분포를 추정한 다음에 추정된 분포를 통해서 새로운 객체가 들어왔을 때 그 객체가 발생할 확률이 매우 높으면 normal로 판별하고, 그렇지 않으면 adnormal로 판별하자!

• 목적: data-driven density function을 추정하자!

1.1. Gaussian Distribution

(1) Gaussian Density Estimation

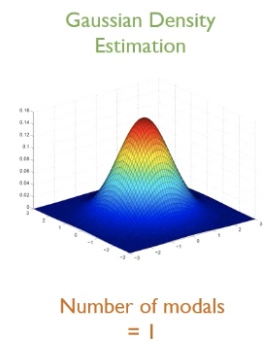
• 다차원 데이터에 대해서 modal의 개수가 1개임.

• 평균 벡터와 공분산 행렬을 추정하는 것이 학습 과정임.

(2) Mixture of Gaussian Density Estimation

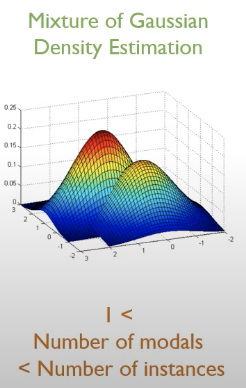
• 가우시안 분포의 결합된 수가 1개보다는 크고, 현재 가지고 있는 학습 데이터의 수보다는 적음.

(3) Kernel Density Estimation

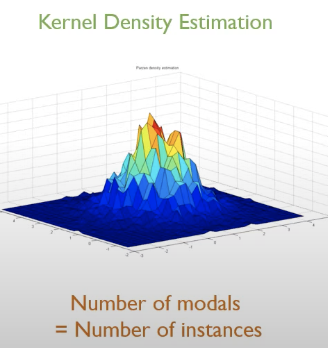
• modal의 개수 = 학습 데이터에 포함되는 normal 데이터의 개수

• 각각의 개체들은 모두 가우시안 분포의 중심임을 가정하고 그로부터 주어진 정상 데이터 영역의 밀도함수를 추정하겠다는 뜻임.

---

1.2. Gaussian Density Estimation

1.2.1. Assume

: 관측치들은 하나의 가우시안 분포로부터 sampling이 되었음.

---

1.2.2. Advantages

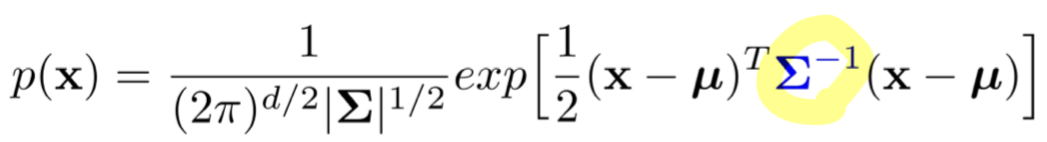
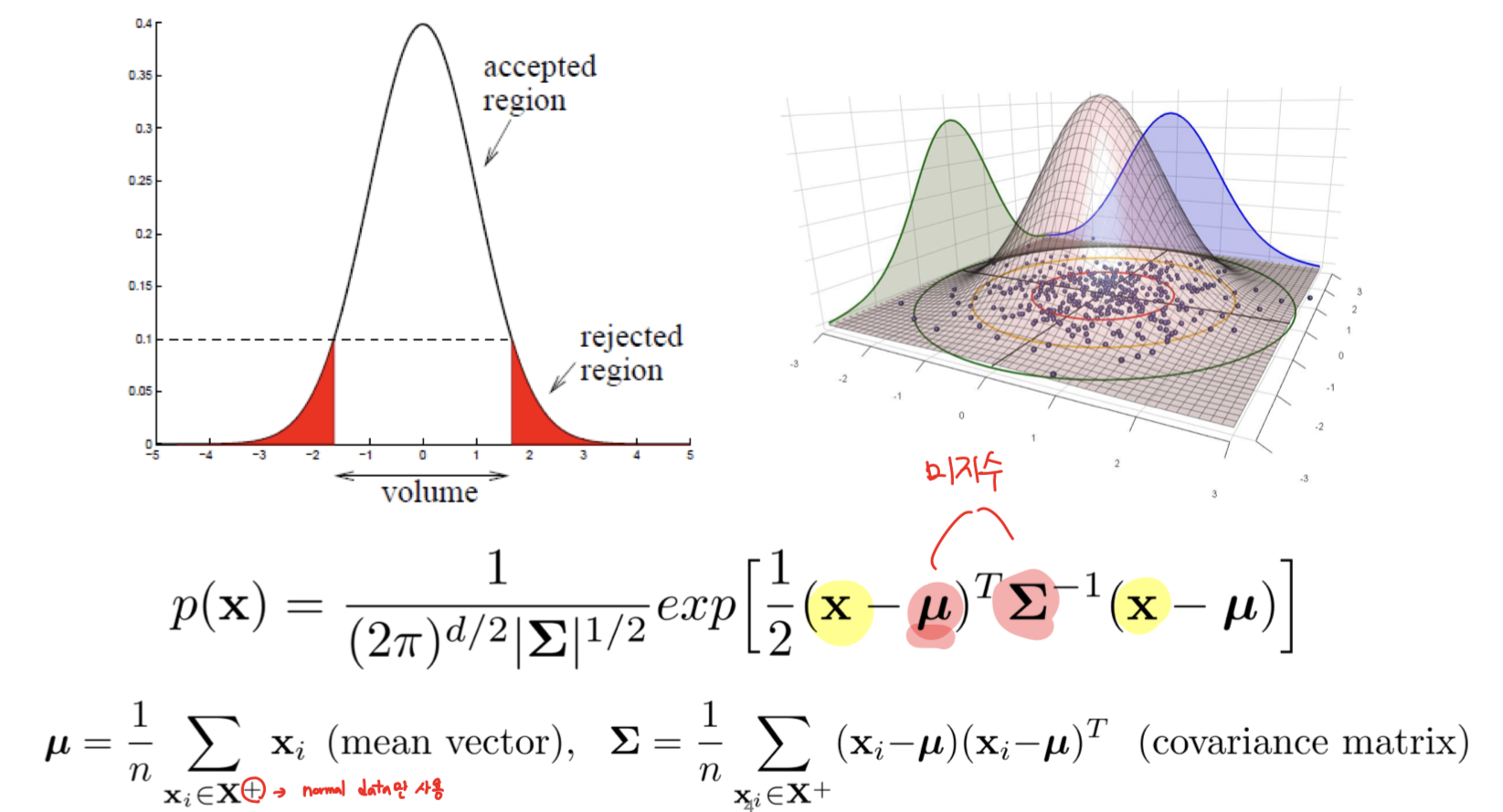
(1) 데이터 변수의 범위에 민감하지 않음. 즉, Robust함.

• 노란색 동그라미인 covariance metrix의 역행렬을 구해주기 때문에 변수에 대한 크기와 측정단위가 영향을 미치지 않음.
  -> 그래서 굳이 normalization을 하지 않아도 됨.

(2) optimal threshold를 자동적으로 계산할 수 있음.

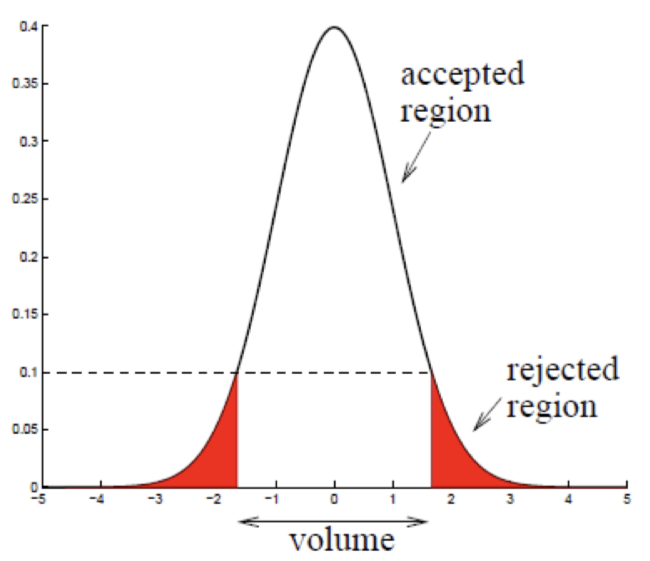
• 처음부터 rejection에 대한 1종 오류를 정의하고 들어갈 수 있음.

---

1.2.3. Parameter estimation

• $\mu$ and $\sigma^2$

• 위 두 미지수에 대해서 최적해 조건을 만족하기 위해서는 일차도함수가 0이여야 함.

---

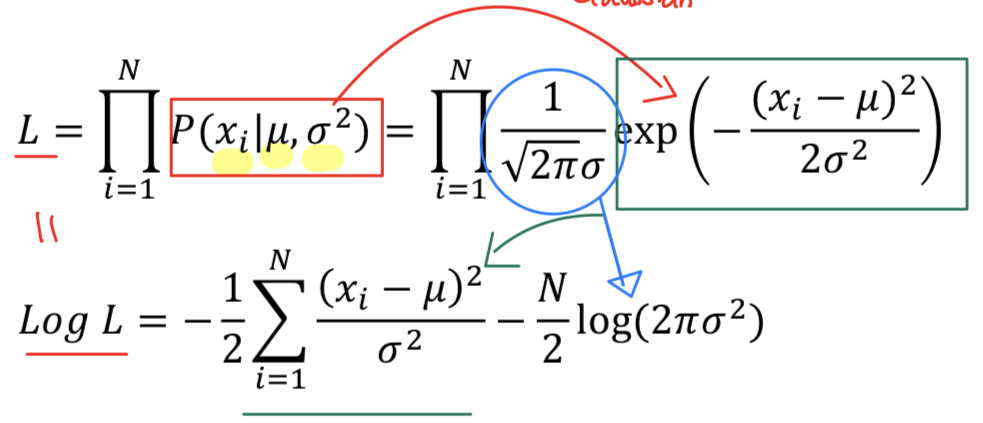
1.2.4. Maximum likelihood estimation

• $\gamma$ = $1\over\sigma^2$

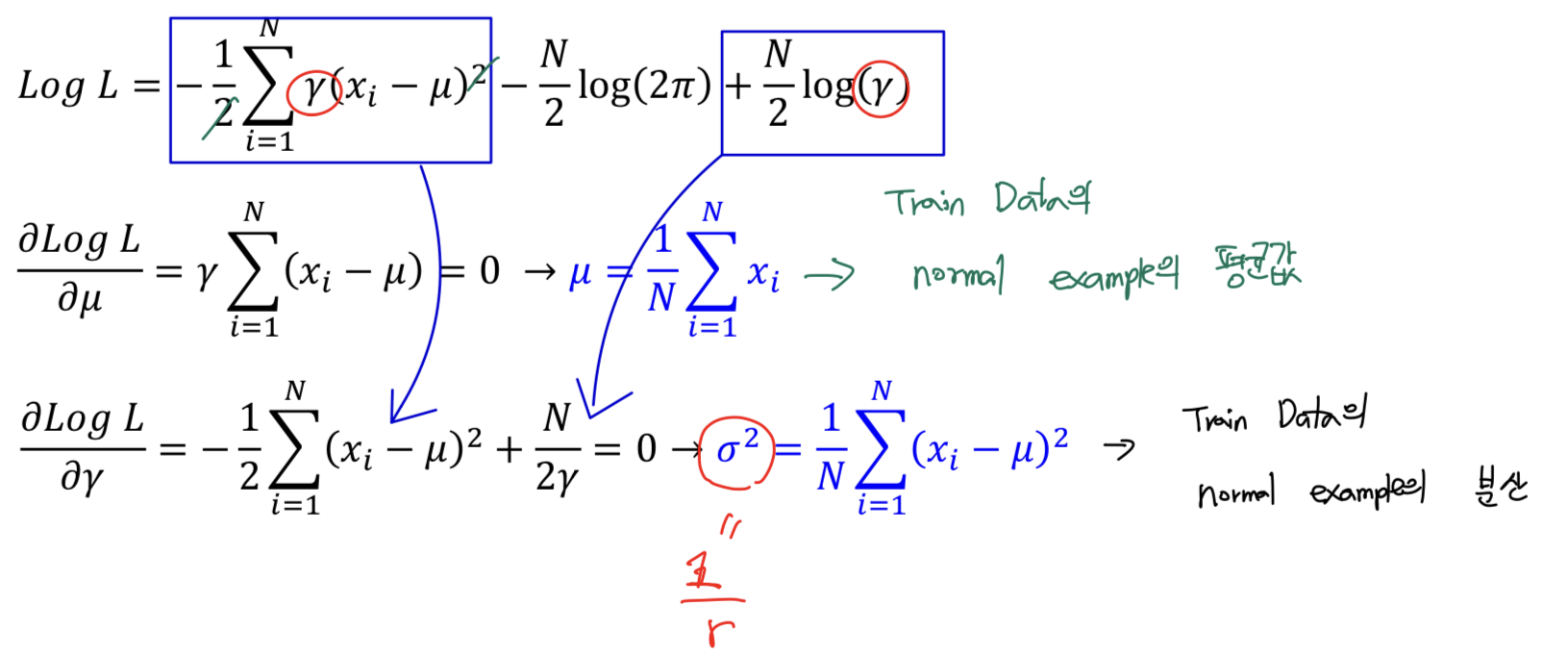
• 치환해서 Log likelihood에 적용함.

• 해당 식을 $\mu$ 와 $\gamma$에 대해서 미분을 하면 Train data의 normal example의 평균값과 분산값이 나오게 됨.

다시 정리를 하면,

• $\mu$ = $1\over N$ $\sum$ $x_i$

• $\sum$ = $1\over N$ $\sum$ ($x_i$ - $\mu$)($x_i$ - $\mu$)$^T$

---

1.2.5. Covariance matrix type

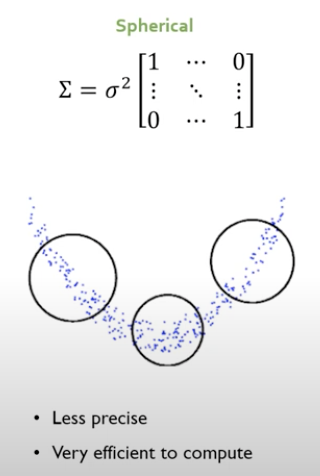
1. Spherical

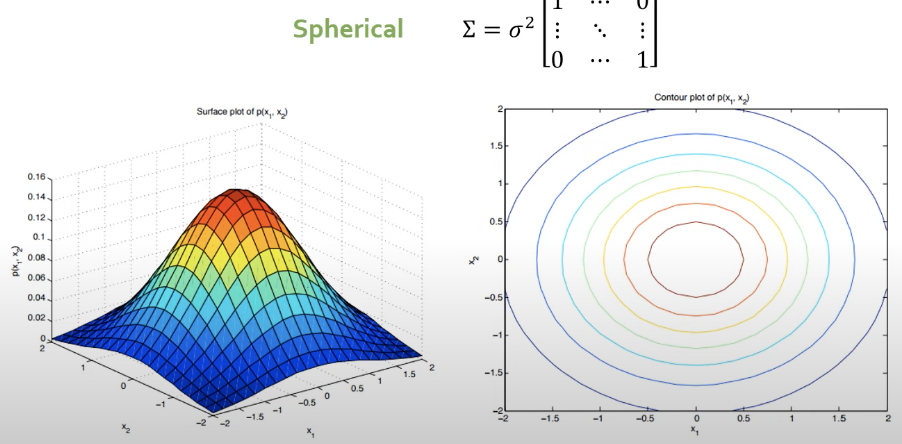
• 오른쪽 그림은 위에서 내려다본 단면으로서 등고선임.

• 데이터를 normalization을 하고 각각의 변수들이 독립이다라는 것을 가정함.

• 축이 수직이어야 함.

2. Diagonal

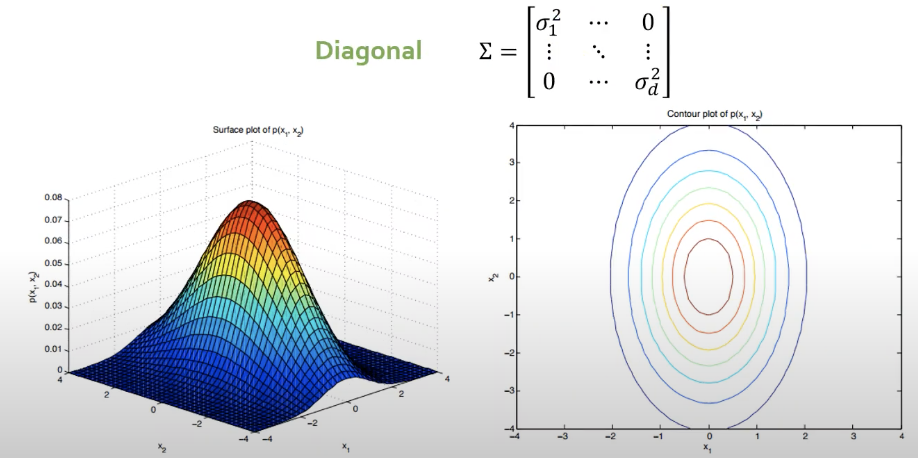
• 각각의 변수들이 독립이라는 가정 말고도 개별적인 변수들의 분산이 다르다는 것을 알 수 있음.

• 타원의 형태

3. Full

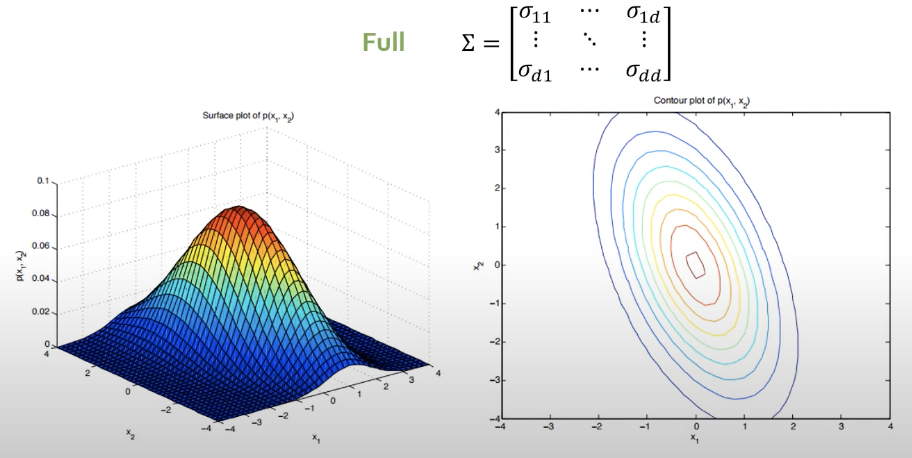
• 모든 과정을 완화하면 Full covariance matrix가 됨.

• 각각의 변수들이 어느정도 상관관계가 있음.

• 등고선을 확인해보면, 수직이 아니라는 것을 확인할 수 있음.

• 데이터가 충분히 많고 covariance matrix가 single하지 않으면 full covariance matrix를 쓰는게 당연히 좋음.
  -> 하지만 현실적인 대안은 Diagonal을 쓰는게 제일 합리적임.
  

4. 정리

• 전체 데이터를 하나의 Gaussian 분포로 가정하고, 거기에서부터 이상치 score를 계산하는 방식임.

• anomaly score = $1$ - $P(x)$
  • 추정된 확률밀도함수로부터 새로운 데이터가 들어왔을 때, 산출되는 확률분포의 값임.
  • 그 값이 낮을수록 이상치일 가능성 ⬆️
  • 그 값이 높을수록 이상치일 가능성 ⬇️

• 모든 데이터가 단 하나의 가우시안 분포로부터 추정된다는 가정은 어려울수 있음.

• unimodal & convex하기 때문에 매우 엄격한 가정

---

2. Mixture of Gaussian Density Estimation

• unimodal -> multi-modal로 바뀜

• 좀 더 bias가 적고 정확한 추정이 가능해짐. 하지만 training에 더 많은 데이터가 필요함.

• Single Gaussian: 미지수: 2개 ($\mu$, $\sigma^2$)

• MoG: 미지수: 3xk개 ($\mu$, $\sigma^2$, $w$)

---

2.1. Componets of MoG

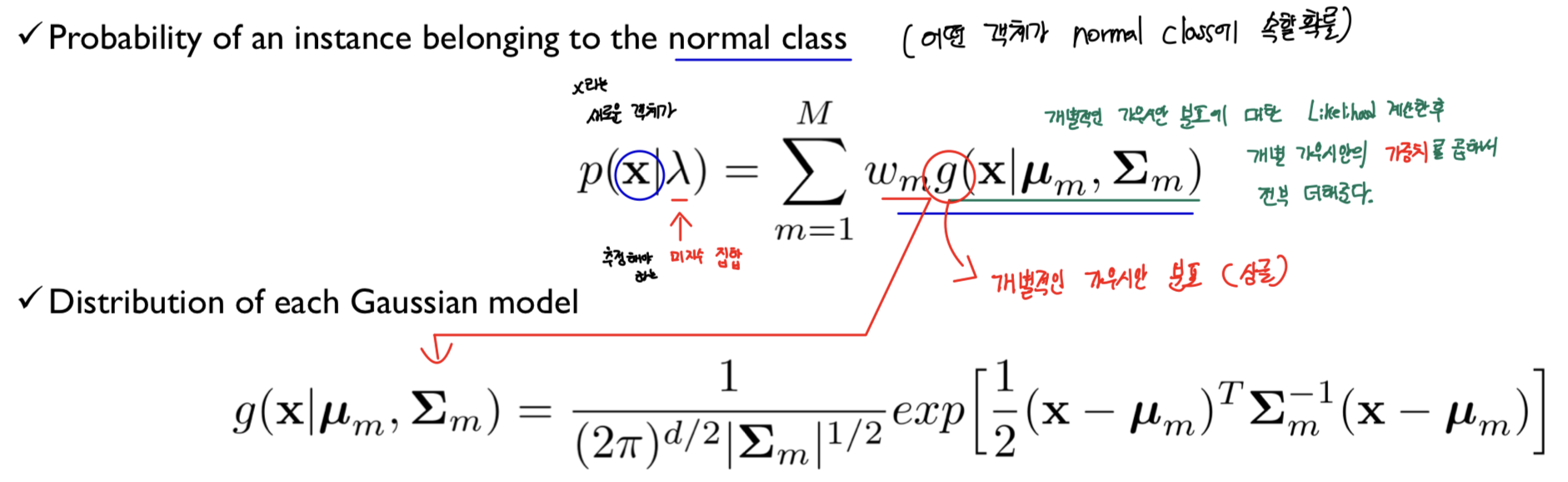
• 개별적인 가우시안 분포에 대한 Likelihood를 계산한 후 개별 가우시안의 가중치를 곱해서 전부 더해줌.

• $g$: 개별적인 가우시안 분포(single)

• $\lambda$: 추정해야 하는 미지수 집합

• $x$: 새로운 개체

---

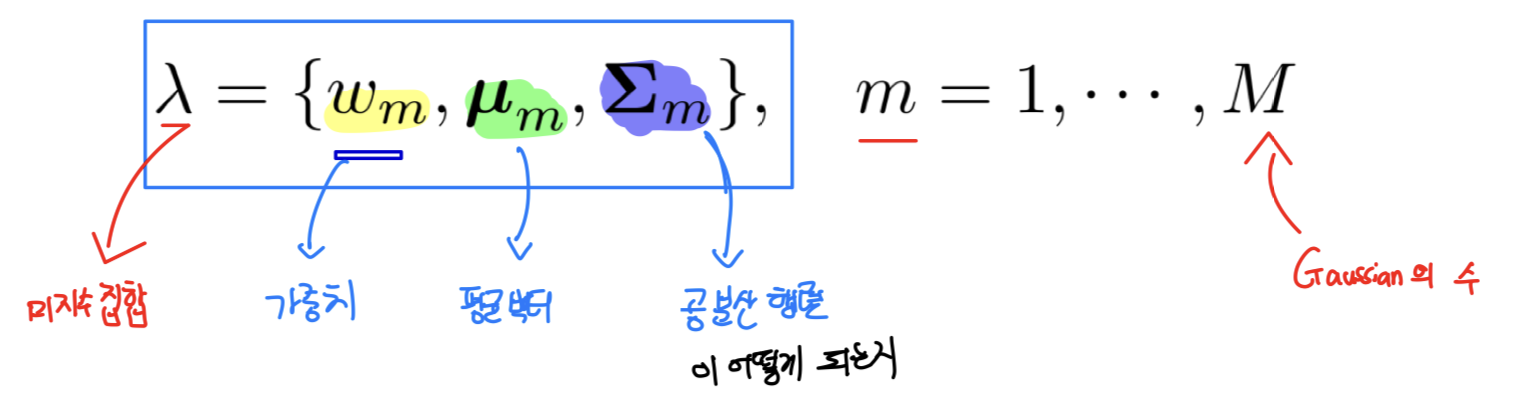
2.2. Expection-Maximization Algorithm

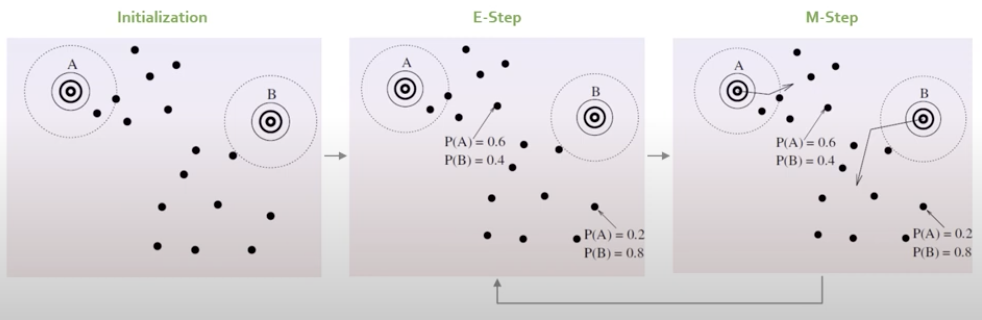
• 한 번에 하나의 미지수만 최적화를 해주자 (EM 알고리즘)

• 한꺼번에 최적화가 아닌 (A 고정-> B 최적화 / B 고정 -> A 최적화) 방식으로 여러번 반복하면 A와 B가 불변하여 수렴

(1) E-Step

• 모수의 현재 추정치가 주어지면 조건부 확률을 계산함.
  -가우시안 고정 -> Parameter Update
  -개체의 확률 -> 고정
  -이것을 반복하다보면 가우시안분포의 $W$, $\mu$,$\sum$을 찾을 수 있음.

(2) M-Step

• E-step에서 찾을 수 있는 예상 가능성을 최대화하도록 모수를 업데이트 진행.

2.2.1. 수식

---

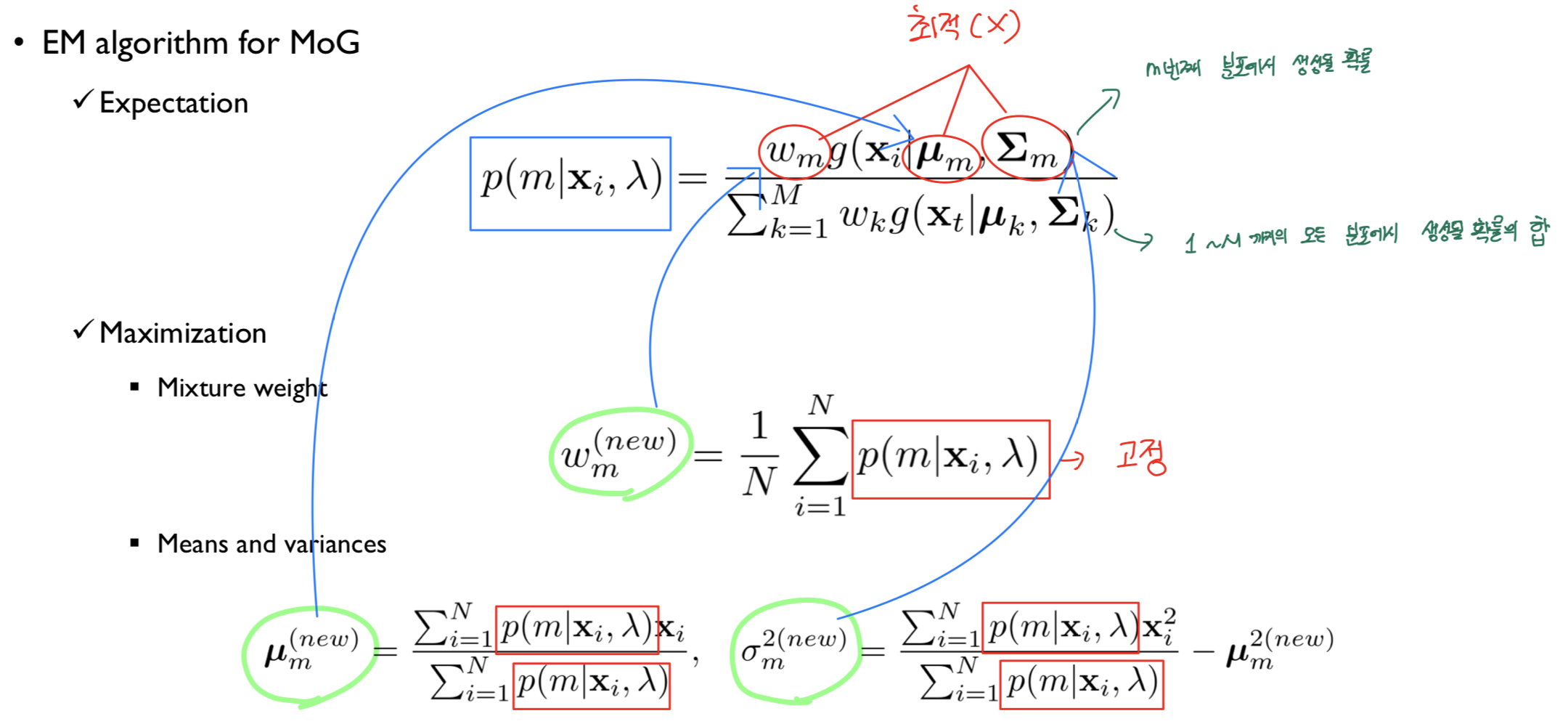
2.3. Covariance Matrix

1. Spherical

2. Diagonal

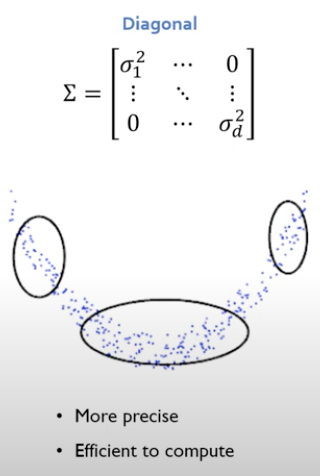
• 제일 현실적임.

3. Full

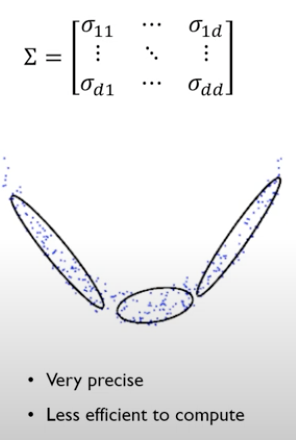
• 자유도가 높음

---

🎯 Summary

• 가우시안 분포에 대한 수식 설명과 EM 알고리즘이 인상깊었음.

• 강의자료와 유튜브를 무료로 볼 수 있게 한 DSBA 연구실에 감사의 인사를 전합니다.

📚 References

• Youtube

• https://www.youtube.com/watch?v=kKZM8bxwQbA, DSBA 연구실 유튜브

• 강의 자료

• https://github.com/pilsung-kang/Business-Analytics-IME654-/blob/master/03%20Anomaly%20Detection/03-2_Anomaly%20Detection_Gauss_MoG.pdf, 강필성 교수님 github