출처: DSBA 연구실 유튜브 와 DSBA 연구실 강의자료 를 참고하면서 스터디를 진행하였습니다.
주제: Anomaly Detection: Parzen Window Density Estimation
1. Kernel-density Estimation
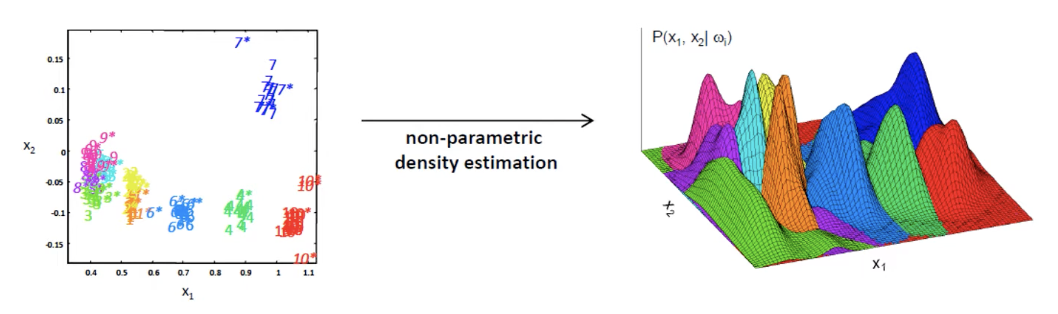
- 기존에는 특정한 파라미터와 가우시안 분포를 가정한 상태에서 주어진 데이터를 해당하는 데이터에 끼워넣었음.
📌 밀도 자체를 특정한 분포로부터 산출되었다는 가정
📌 가우시안 분포의 평균, 분산, 표준편차를 구하는 것이 핵심
- Kernel-density Estimation은 사전에 정의된 분포가 아닌, 데이터 자체로부터 개별적인 개체들의 확률을 추정하고자 함.
=> non-parametric density estimation이라고도 부름
- 위의 그림처럼 single data가 들어왔을 때 발생할 확룰을 추정하는 것임.
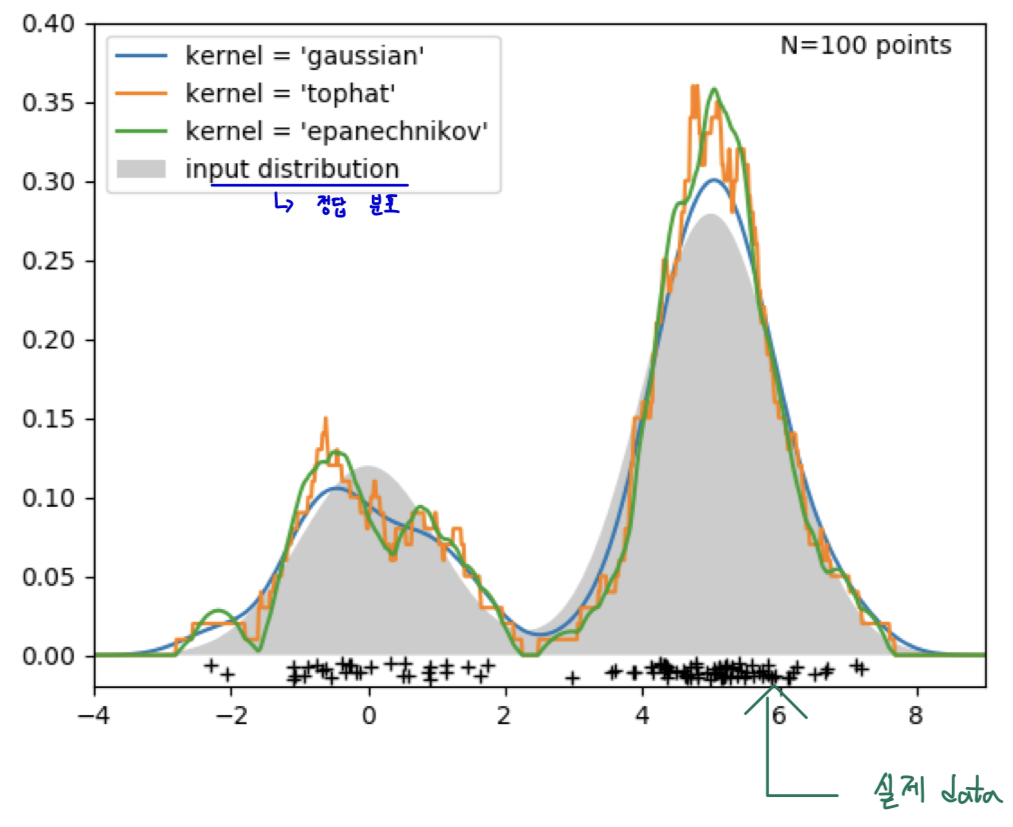
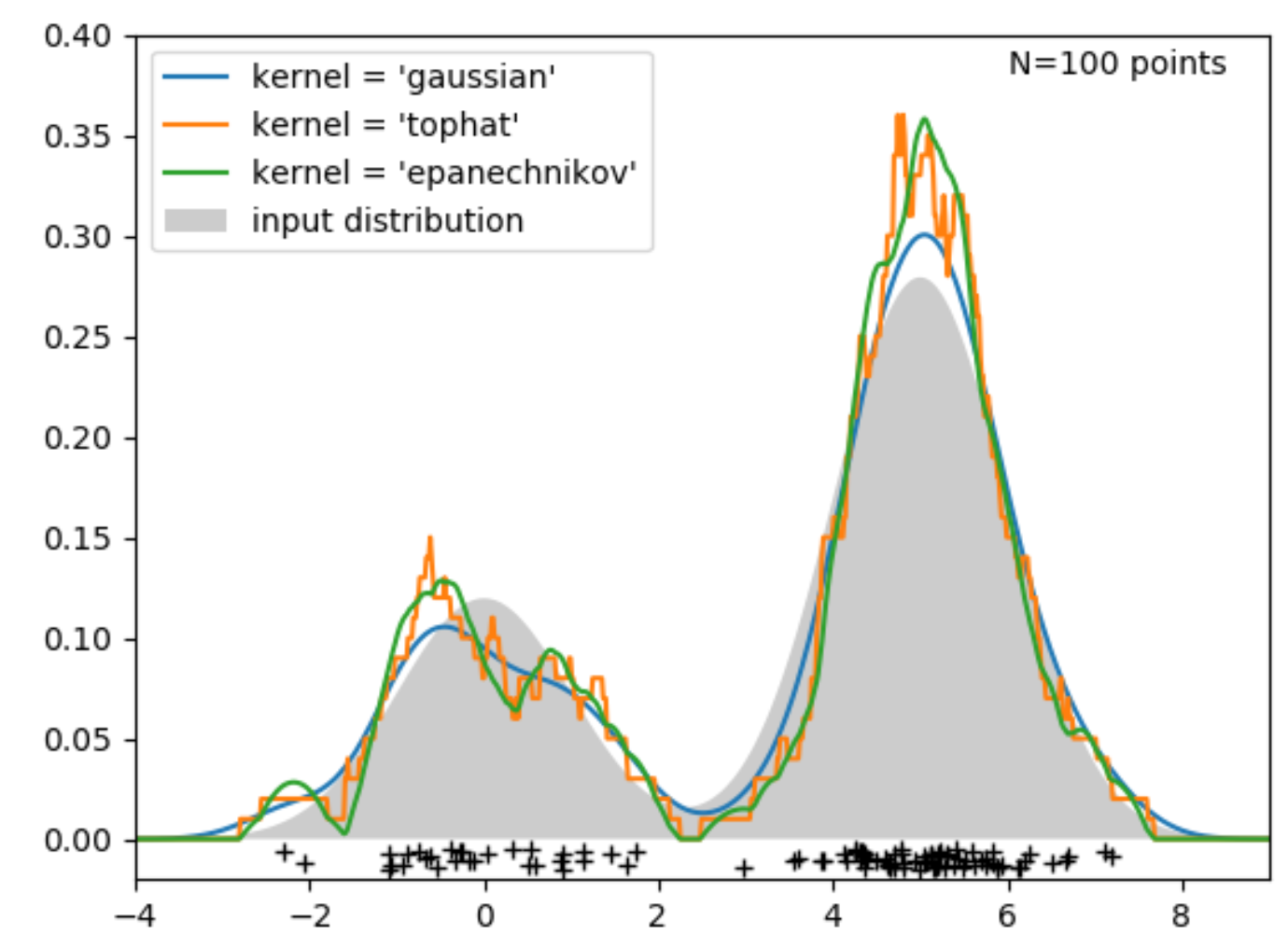
- 어떠한 Kernel을 쓰냐에 따라서 추정되는 분포의 모양이 달라지는 것을 볼 수 있음.
📬 정리
- Kernel-density Estimation은 확률 밀도를 어떠한 분포로 가정하지 않고 현재 우리가 가지고 있는 데이터와 우리가 보고자 하는 영역의 크기 그리고 그 영역 안에 존재하는 개체수를 가지고 근사 시키는 것이 목표임
1.1. Proof
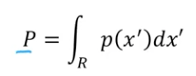
- 특정 R에 들어갈 확률을 구하면 다음과 같이 나타낼 수 있음.
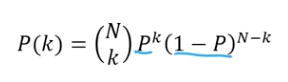
- 는 영역에 들어올 확률을 의미하고, 위의 식은 이항분포 식을 의미함.
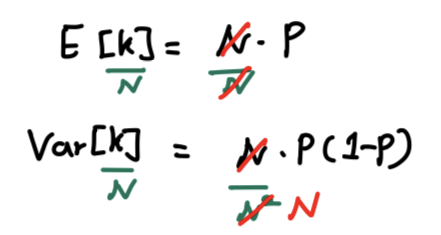
- 평균과 분산을 각각 구하면, / 임.
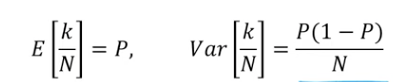
- 양변을 으로 나누면, 다음과 같음. 특히 분산에서는 이 빠져 나오면 으로 나오게 됨.
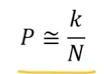
- 이 무한대로 가고 분산이 작아질수록 P는 다음과 같이 근사할 수 있음.
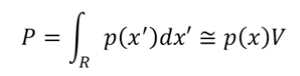
- 이 매우 작은 영역이여서 가 급격하게 변하지 않는다고 가정한다면, 해당 적분값은 위와 같이 임.
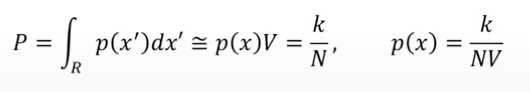
- 는 특정 영역에 개체가 속할 확률값을 의미함.
📬 정리
- 특정한 확률분포 상에서 관심 있는 영역 안에 region에 떨어지는 확률값은 로 근사할 수 있음.
- = 라고 말할 수 있음.

- : 해당하는 x를 표현하는 주변 volume의 크기
- : 전체 데이터 수
- : 영역 안에 들어가있는 실제 개체 수
📌 의 크기가 커지고 의 영역이 작을수록 정확해짐
📌 의 크기가 작아야지만 내에서의 확률밀도함수 값은 균일하다는 가정을 만족시키기 때문임.
📌 Fix + determine from the data
: Kernel-density estimation
=> 영역을 고정한 상태에서 그 안에 들어가 있는 개체수를 이용해서 밀도 추정을 하는 방식임.
📌 Fix + determine from the data
: k-nearest neighbor density estimation
2. Parzen Window Density Estimation
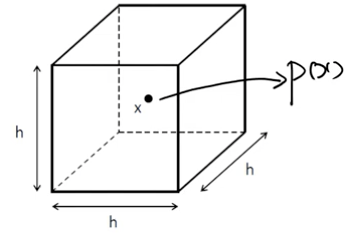
- 는 항상 가운데 있고, 사이드 변은 이며 4차원 이상부터는 머릿속으로 그림을 그릴 수 없기 때문에 hypercube라고 칭함.
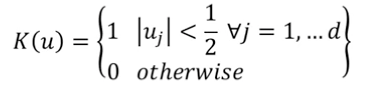
- kenerl 부분이 보다 작으면, 1 반환
- kernel 부분이 보다 크면, 0 반환
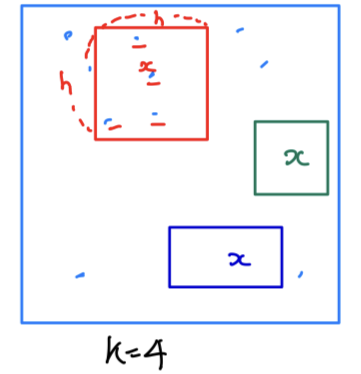
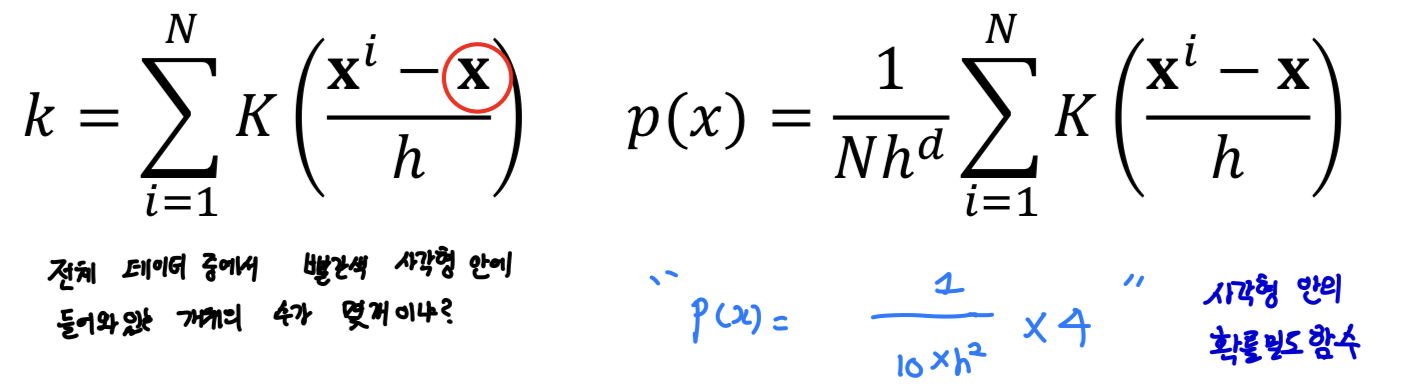
- 영역을 옮겨가면서 확률밀도함수를 계산함
=> Parzen Window Density Estimation
📌 실제 데이터의 형태가 특정 분포를 따르지 않는다.
문제점
- discontinuities 불연속적임.
- 밑의 사진처럼 기준으로 짤라져버리기 때문에 문제가 발생함.
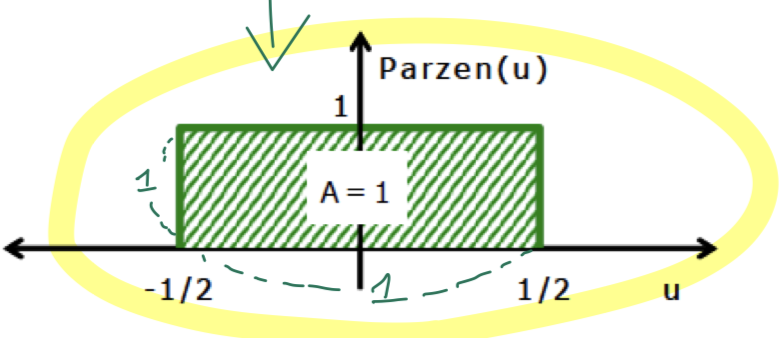
개선
- Smooth Kernel function 사용
- 해당 영역 안에서의 적분값이 1이면 됨.
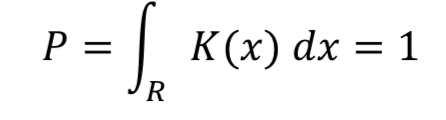
2.1. Example of smooth kernels
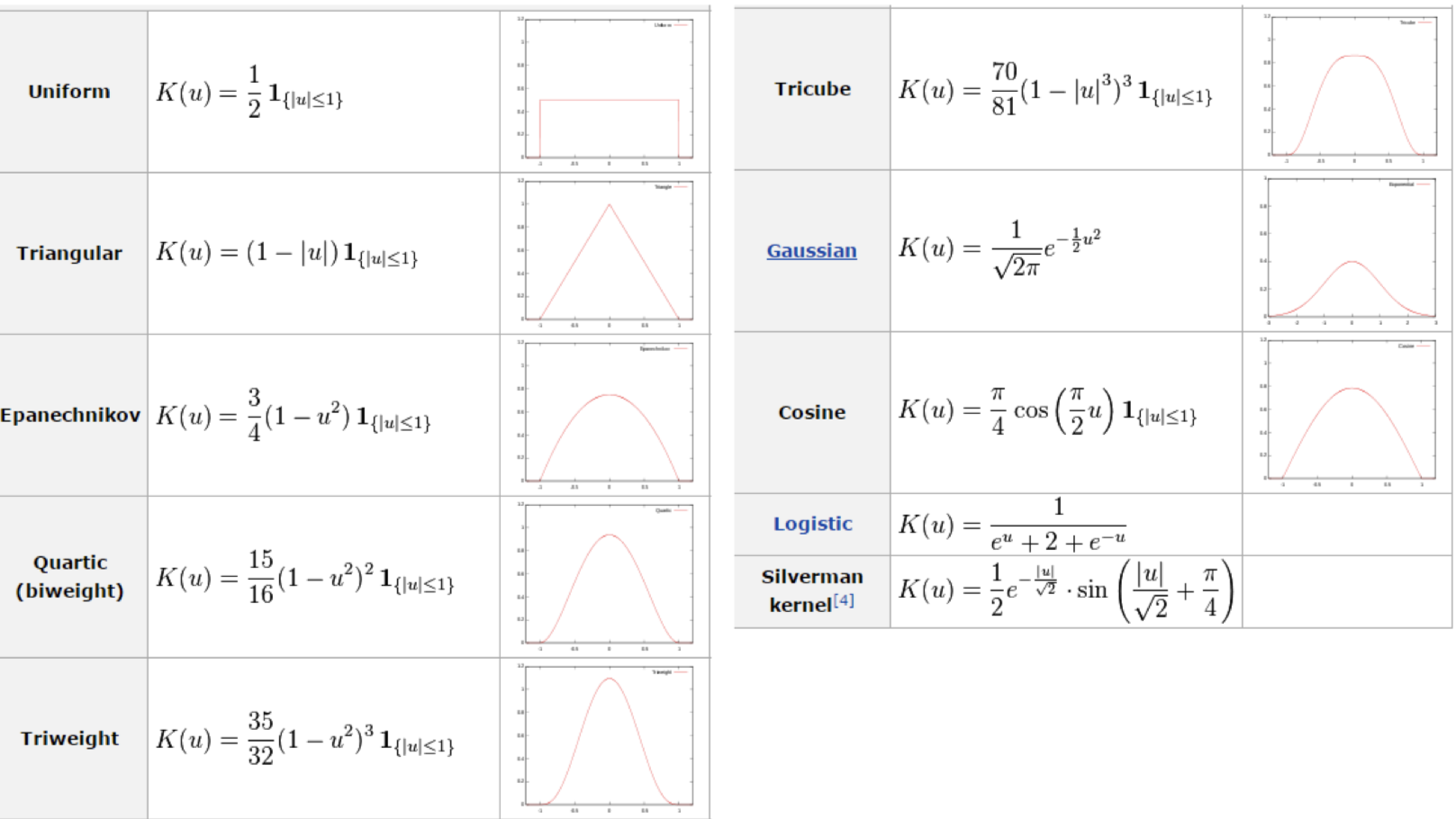
2.2. Smoothing parameter (bandwidth) h
📌 Small h
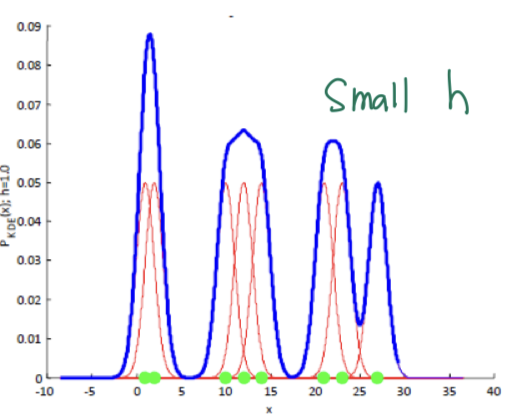
- h 값이 작으면 더 세밀한 추정을 얻을 수 있지만 너무 작으면 노이즈에 민감해질 수 있음.
📌 Large h
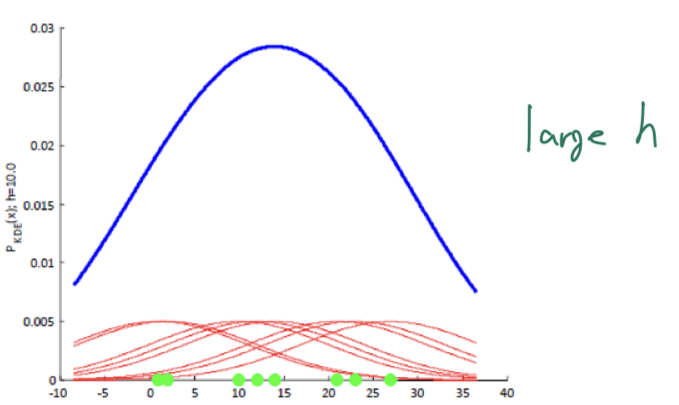
- h 값이 크면 노이즈에 덜 민감해지지만 추정이 뭉뚱그려질 수 있음.
- likelihood를 최대화할 수 있는 bandwidth를 찾아내는 것이 학습과정에 필요한 절차 중 하나임.
2.3. Density Estimation Summary
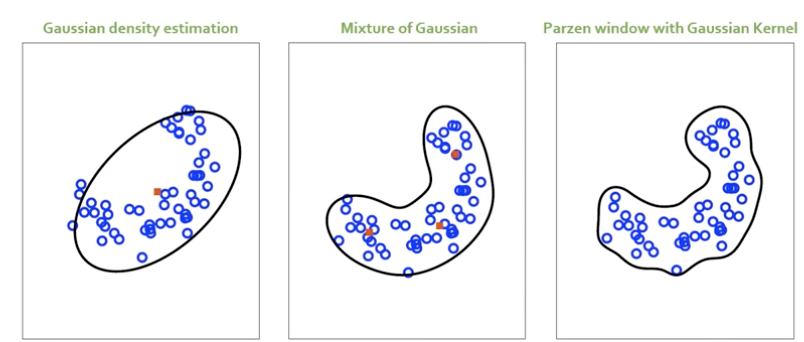
📌 밀도 기반 이상치 탐지
- 데이터로부터 밀도를 추정해서 밀도가 낮은 영역을 이상치로 판별하자!
🎯 Summary
- 비모수적 밀도 추정 방법 중 하나로 앞에 나왔던 가우시안 분포와 달리 어떤 확률 분포 함수를 가정하지 않고도 데이터의 분포를 추정할 수 있었음.
-
각 데이터 포인트를 "window" 또는 "kernel"로 대체하고, 이들을 합쳐 전체 데이터의 밀도를 추정하는 것이 핵심임.
-
Parzen Window 방식에서 R-CNN에서 나왔던 Sliding Window 방식과 매우 유사하다는 것을 느꼈음.
- 다차원 데이터에 대한 이상치 탐지에 특히 유용하며, 특히 데이터의 구조가 복잡하거나 분포에 대한 사전 지식이 없는 경우에 활용할 수 있음.
- 데이터의 밀도를 추정한 후, 낮은 밀도영역에 위치한 데이터 포인트는 이상치로 간주 가능.
- 강의자료와 유튜브를 무료로 볼 수 있게 한 DSBA 연구실에 감사의 인사를 전합니다.
📚 References
- Youtube
- https://www.youtube.com/watch?v=rddQT5vxwrg&list=PLetSlH8YjIfWMdw9AuLR5ybkVvGcoG2EW&index=18, DSBA 연구실 유튜브
- 강의 자료
