푸드 파이트 대회
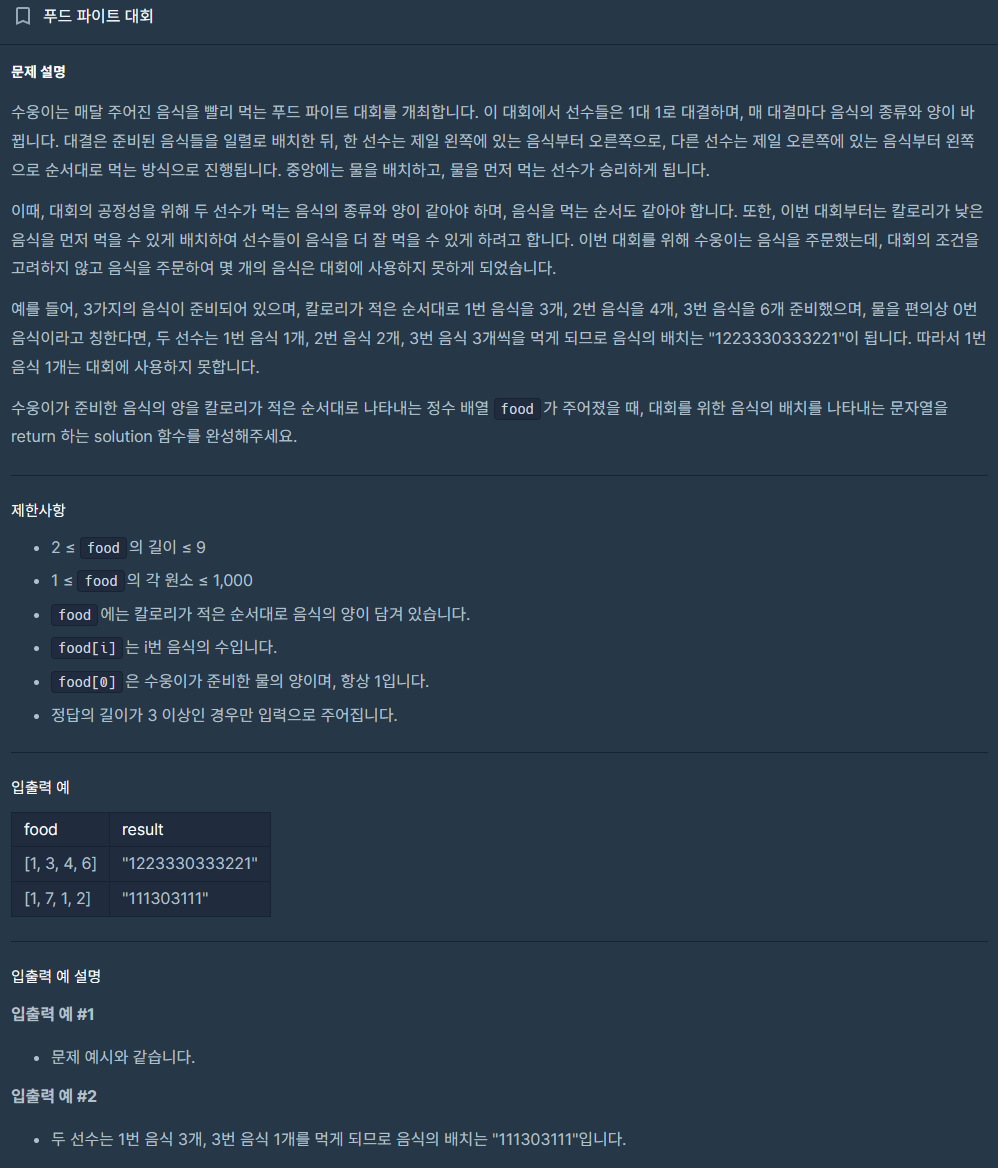
아니 뭔놈의 지문이 이렇게 길어...
나의 풀이
function solution(food) {
var answer = '';
const lengthOfFood = food.length;
let end = '';
for ( let i = 1 ; i < lengthOfFood ; i++ ){
const amount = food[i]
const n = Math.floor(amount/2)
const reapeatI = String(i).repeat(n);
answer += reapeatI;
end = reapeatI+end
}
answer += '0' + end
return answer;
}시간복잡도를 어떻게 계산해야할지 몰라서 GPT한테 물어보니까 라고한다.
즉, 이므로 다는 더 좋은 시간복잡도를 가지는것같다.
다른 사람의 풀이
function sol1(food) {
let res = '';
for (let i = 1; i < food.length; i++) {
res += String(i).repeat(Math.floor(food[i]/2));
}
return res + '0' + [...res].reverse().join('');
}내가 한것보다 이게 훨씬 좋은것같다...
function sol2(food) {
var answer = '';
let arr = [];
food.map((f,i) => {
f = f % 2 == 0 ? f : f -1;
for(let j=0;j<f/2;j++){
arr.push(i);
}
});
answer = arr.join('') + 0 + arr.reverse().join('');
return answer;
}repeat없이 for문을 돌렸다. 이래되면 시간복잡도가 이 될것같아서 안했던 것이다.
function sol3(food) {
var answer = '0';
for(var i=food.length-1;i>0;i--){
if(food[i]>1) {
for(var j=1;j<=food[i]/2;j++){
answer = i+answer+i;
}
}
}
return answer;
}이걸 조금 개량하는 것도 좋을 것같다 아래와같이...
function sol00(food) {
var answer = 0;
const lengthOfFood = food.length;
for ( let i = 1 ; i < lengthOfFood ; i++ ){
const amount = food[i]
const n = Math.floor(amount/2)
const reapeatI = String(i).repeat(n);
answer = reapeatI + answer + reapeatI;
}
return answer;
}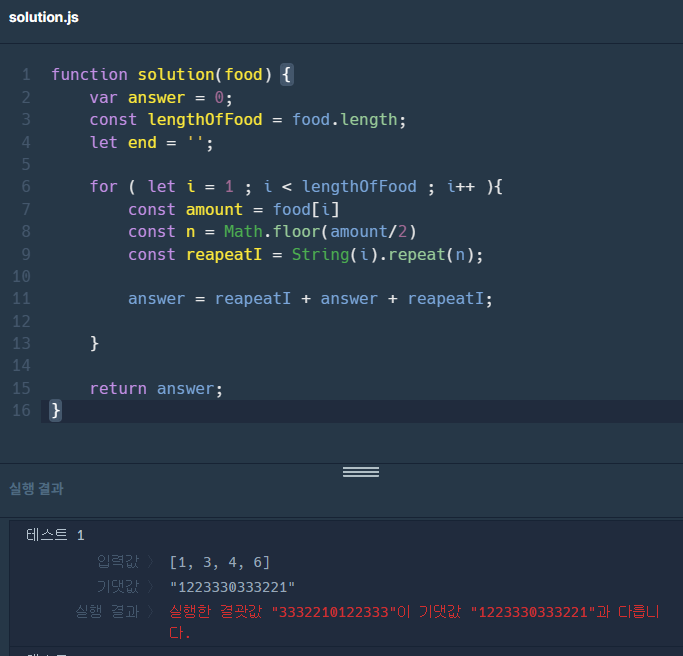
아 생각한것과 반대로 나온다...
조금 바꾸면 정답이 나오긴하는데 내가 원하는건 for문안에서 해결하는 것이었기 때문에 원하는 방식으로는 안된다. 일단 속도 비교를위해서 넣어두기만하자
속도 비교

10만회에서 100만회로 늘릴 생각이었는데 너무 오래걸려서 1만회로 줄여버렸다.
sol0, 00은 6~7배 정도 차이나는데 나머지는 10배가 차이난다. 아무래도 최악의 경우로 구현된 경우인것같다.
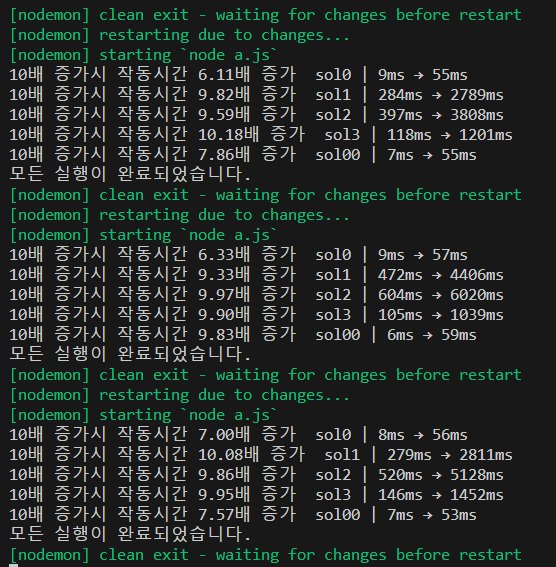
코드를 조금 수정해서 가독성을 올려봤다.
한 세트마다 입력값은 랜덤으로 생성해서 같은걸 쓰고
다음 세트에서는 다른 랜덤값을 생성하는 방식이다.
주목할만한점으로는 다른 사람의 코드와 내 코드를 같이 합친 sol00이 빠르기는 제일 빠르지만 어떨때는 증가율이 크다는 것이다.
숫자의 표현
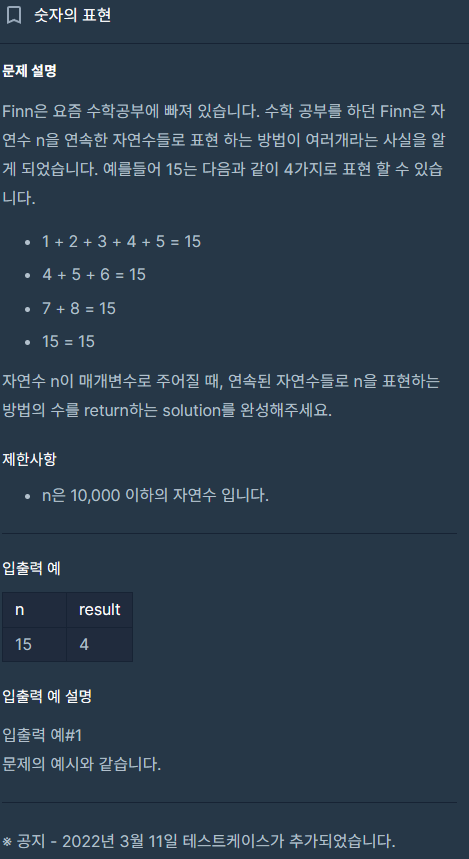
무식하게 하나하나 더하는 방법이 있지만 이런건 수학을 이용하면 쉽게 풀린다...
그런데 어떻게하지? ㅋㅋㅋ 이래서 정수론을 공부해야하는구나...
한 블로그를 찾았고 답은 관심 없으니 쭉쭉 내렸다.
a + (a+1) + (a+2) + ... + (a+k-1) = k(2a+k-1)/2 = n
a <= n
k < n
a,k : 자연수
n/k 가 자연수이려면 : k는 n의 약수여야 한다.
(1-k)/2 가 정수가 되려면 : 1-k 가 짝수여야 하므로 k는 홀수여야 한다.
k < n위의 조건에 맞춰서 코드를 짜자
나의 풀이
function sol0(n) {
var answer = 0;
const factor = []
for (let i = 0 ; i <= n ; i++){
if (n%i === 0 && i%2 === 1){
factor.push(i)
}
}
answer = factor.length
return answer;
}위의 수의 성질을 만족하는 것을 JS 코드로 풀이했다.
다른 사람의 풀이
function sol1(num) {
var answer = 0;
for (var i = 1; i <= num; i++) {
if ((num % i == 0) && (i % 2 == 1)) {
answer++;
}
}
return answer;
}내가 한 것보다 무조건 효율적인 풀이다.
function sol2(num) {
var answer = 0;
var k = 0;
while((k*(k-1)/2)<=num){
if(Number.isInteger((num/k)-(k-1)/2) && ((num/k)-(k-1)/2 != 0)){
answer++;
}
k++;
}
return answer;
}수학적 이론은 같으나 정리가 덜 되었다.
속도 비교
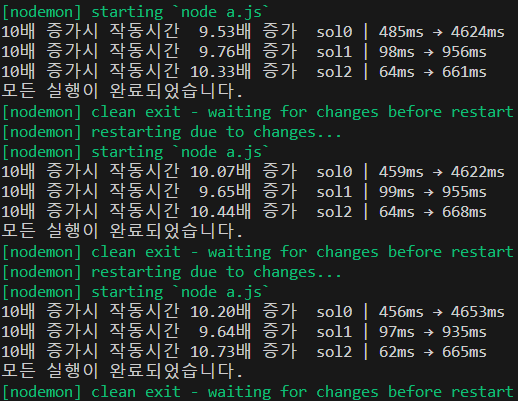
어째서인지 정리를 덜 한 녀석이 더 빠르게 나왔다.
for보다 while이 더 빠른 것인가?
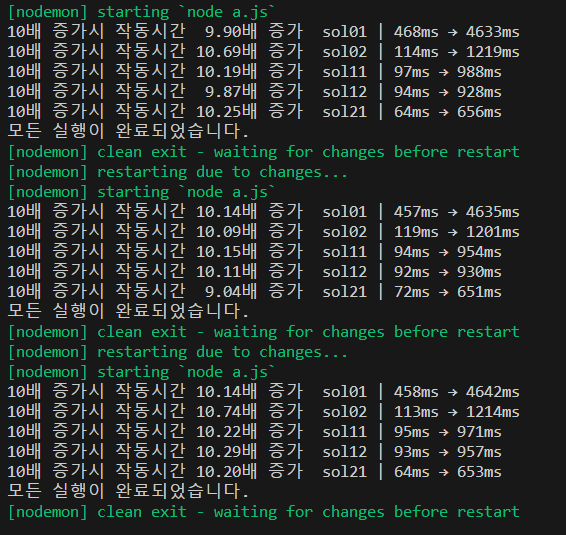
코드들을 while문으로 고치고 해봤다.
나의 코드의 경우 거의 4배 차이가 나고
다른사람의 코드1도 2%정도뿐이긴하지만 빨라졌다.
아쉽게도 어떤 것을하든 10배가 증가하는것으로 봐서는 거의 모든 경우의 수에 대해서 계산을 해야함을 알 수 있다.
그리고 해당 조건에서는 for문보다 while문이 더 빠름을 알 수 있다.
공부하며 느낀 점
- 값을 쌓아놓고 붙이는것 보다는 그때그때 붙이는게 빠르다.
- for문 보다는 while문이 더 빠를때 도 있다.
반대의 경우도 없는지 확인해야겠다. - 인 코드가 있을 때 그 횟수를 10회 늘리더라도, 입력값이 뭐냐에 따라서 실행시간이 달라질 수 있다.
- 수학적으로 정리를 덜 한것이 오히려 더 빠를 수 도 있다.
